А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 6 страница

Заметим, что понятия напряжения, токи и сопротивления различных последовательностей условны. Эти понятия возникают из сущности метода расчета – метода симметричных составляющих.

4.3. Сопротивления прямой, обратной и нулевой последовательностей

для элементов схем замещения

Общие замечания

Сопротивления прямой последовательности элементов схемы замещения - это те же сопротивления, которые вводились в схему замещения при рас-

чете симмеричного режима, например трехфазного к.з.

Поэтому то, что обозначалось при расчете симметричных режимов через 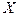, в схеме прямой последовательности обозначают как .

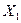Для всех элементов схемы, которые не имеют вращающих частей, сопро-

тивления обратной последовательности совпадают с их значениями в схеме прямой последовательности.

Сопротивления нулевой последовательности элементов схемы могут существенно отличаться от первых двух сопротивлений (прямой и обратной последовательностей), так как циркуляция токов нулевой последовательно-

сти возможна лишь в том случае, если имеется путь по четвертому проводу или в земле.

Рассмотрим порядок определения сопротивлений обратной и нулевой последовательностей для основных элементов электрических схем.

Синхронные машины

Магнитный поток, созданный токами обратной последовательности синхронной частоты, вращаясь относительно ротора с двойной синхронной частотой, встречает на своем пути непрерывно изменяющееся магнитное сопротивление. Это обусловлено магнитной несимметрией ротора и тем, что наведенные в продольных и поперечных контурах ротора токи создают различные ответные реакции.

Таким образом, при неизменной н.с. статора магнитный поток обратной последовательности гармонически изменяется с двойной синхронной частотой в пределах между его набольшим и наименьшим значениями, разница между которыми зависит от степени несимметрии ротора.

Для синхронной машины без демпферных обмоток ранее было получено выражение для реактивности 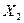(§ 3.5.1.)

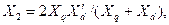(4.11)

которая по существу представляет собой реактивность обратной последова-

тельности.

В качестве приближенных соотношений можно принимать:

1) для машин без демпферных обмоток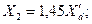

2) для турбогенераторов и машин с демпферными обмотками в обеих осях ротора 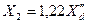или еще более упрощенно .

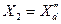Реактивность нулевой последовательности принимается равной

.

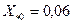Асинхронные двигатели

Если в нормальных условиях асинхронный двигатель работает со ско-

льжением 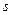, то по отношению к магнитному потоку обратной последовательности синхронной частоты ротор двигателя будет иметь скольжение ( 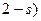. Следовательно, сопротивление обратной последовательности асинхронного двигателя представляет его сопротивление при скольжении ( ).

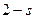При изменении скольжения от нуля до единицы реактивность двигателя в начале резко падает, а затем ее снижение весьма незначительно (при 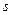> ), что позволяет практически считать

, (4.12)

то есть реактивность асинхронного двигателя принимается равной его так называемой реактивности короткого замыкания (относительная величина которой близка к обратной величине кратности номинального пускового тока).

Реактивность нулевой последовательности асинхронного двигателя, как и синхронных машин, определяется только рассеянием статорной обмотки и существенно зависит от типа и конструкции последней.

Надежные значения этой реактивности могут быть получены преимущественно только опытным путем или по данным завода-изготовителя.

Обобщенная нагрузка

Реактивность обратной последовательности обобщенной нагрузки зависит от характера приемников электроэнергии и относительного участия каждого из них в рассматриваемой нагрузке.

Для средней типовой промышленной нагрузки можно принять, что основная ее часть состоит из асинхронных двигателей, реактивность обратной последовательности которых практически та же, что и в начальный момент внезапного нарушения режима.

Поэтому для реактивности обратной последовательности обобщенной

нагрузки можно принимать в практических расчетах

, (4.13)

считая ее отнесенной к полной рабочей мощности в МВА данной нагрузки и среднему номинальному напряжению той ступени, где она присоединена.

В связи с тем, что обобщенная нагрузка включает в себя низковольтную сеть и понижающие трансформаторы, определяющие в основном ее сопротивление нулевой последовательности, то привести какие-либо средние значения этого сопротивления невозможно.

Трансформаторы

Значения сопротивлений нулевой последовательности трехфазных силовых трансформаторов зависят от конструкции магнитопровода и схемы соединения обмоток. На рис.4.2, 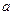, , 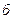, , 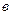, 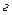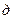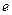приведены основные схемы соединения обмоток трехфазных силовых трансформаторов и соответствующие им схемы замещения нулевой последовательности. Короткое замыкание предполагается на стороне I.

Справа, против каждого варианта соединения обмоток показаны схемызамещения трансформатора (без учета активных сопротивлений) для токов нулевой последовательности.

Рис.4.2.

Из рис.4.2, 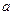видно, что для трансформатора, если к.з. происходит со стороны обмотки, соединенной в звезду с изолированной нейтралью или треугольник, сопротивление нулевой последовательности 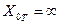. Следовательно, конечная, хотя иногда и очень большая, реактивность нулевой последовательности трансформатора может быть только со стороны обмотки, соединенной в звезду с заземленной нейтралью.

При соединении обмоток по схеме звезда с нулем/треугольник (рис.4.2., 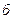) э.д.с. нулевой последовательности трансформатора целиком расходуется на проведение тока той же последовательности только через реактивность рассеяния обмотки, соединенной трегольником, так как этот ток не выходит за пределы данной обмотки в соответствии с первым законом Кирхгофа.

В схеме замещения это отражают закорачиванием ветви с 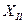на землю. Потенциал, равный нулю, на конце ветви 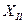схемы замещения не указывает на искусственный перенос заземления нейтрали, как это иногда ошибочно воспринимают; он только соответствует условию, что данной ветвью схемы замещения трансформатора заканчивается путь циркуляции токов нулевой последовательности.

Поэтому электрическая сеть, присоединенная со стороны треугольника, не входит в схему нулевой последовательности даже в том случае, если в ней имеются заземленные нейтрали. Такой трансформатор входит в схему замещения нулевой последовательности только реактивностью прямой последовательности .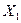

ков нулевой последовательности возможна, так как обеспечен путь для тока нулевой последовательности,рис.4.2, 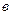) на стороне обмотки 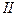.Такой трансформатор входит полной схемой в схему замещения нулевой последовательности.

Если же этого пути нет, то 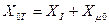, что соответствует режиму холостого хода трансформатора. Аналогично определяется реактивность нулевой последовательности для трансформатора при соединении его обмоток звезда с нулем/звезда с изолированной нейтралью.

Значение 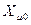зависит от конструкции трансформатора.

Для группы однофазных, трехфазных четырехстержневых и броневых трансформаторов условия для магнитного потока практически те же, что и при питании трансформатора от источника напряжения прямой последовательности. Следовательно, в соответствии с принятым ранее допущением (см.§ 2.2.1.) можно считать .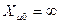

Иные условия имеют место в трехфазных трехстержневых трансформаторах, где магнитные потоки вынуждены замыкаться через изолирующую среду и кожух трансформатора.

Для проведения магнитного потока по пути со столь большим магнитным сопротивлением необходим большой ток намагничивания.

Следовательно, реактивность 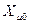у трансфораторов такой конструкции должна быть существенно меньше 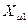. В зависимости от конструкции этого типа трансформатора она находится в пределах: .

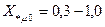Имея в виду, что величина 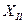значительно меньше 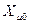, можно практически считать, что и для трехстержневого трансформатора с соединением обмоток звезда с нулем/треугольник .

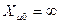В табл.4.1 сведены изложенные выше указания относительно оценки величины реактивности нулевой последовательности двухобмоточных трансформаторов.

Основные варианты соединения обмоток трехобмоточных трансформа торов и соответствующие им схемы замещения нулевой последовательности, считая 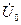приложенным со стороны обмотки 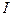приведены на рис.4.2, , , .

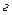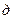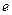У трехобмоточных трасформаторов одна из обмоток, как правило, соединена в треугольник. По этому для них всегда можно принимать .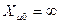

В варианте рис.4.2, 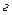ток нулевой последовательности в обмотке отсутствует, следовательно, в этом случае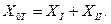

Таблица 4.1

Реактивность 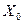двухобмоточных трансформаторов

Тип трансформатора и соединение его обмоток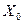
Трансформатор любого типа с соединением обмоток звезда с нулем/треугольник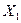
Трехфазная группа из однофазных трансформаторов, трехфазный четырех- пятистержневой трансформатор с соединением обмоток звезда с нулем/звезда с изолированной нейтралью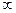
То же с соединением обмоток звезда с нулем/звезда с нулем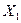
Трехфазный трехстержневой трансформатор: а) с соединением обмоток звезда с нулем/звезда с нулем; б) то же с соединением обмоток звезда с нулем/звезда с нулем	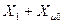по рис.4.2, в

В варианте рис.4.2, 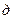предполагается, что путь для тока нулевой последо-

тельности на стороне обмотки 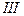обеспечен. В этом случае в схему нулевой последовательности трансформатор должен быть введен своей схемой замещения (трехлучевая звезда).

Наконец, в варианте рис.4.2, 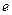компенсация тока нулевой последователь-

ности обмотки 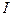осуществляется токами, наведенными в обмотках 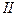и 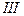. В этом случае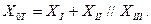

В общем случае нейтраль может быть заземлена через некоторое сопротивление 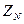. При этом следует учитывать, что сопротивления, устанавливаемые в цепи нейтрали трансформаторов, генераторов и других элементов сети, вводятся в схему нулевой последовательности утроенной величиной. При глухозаземленной нейтрали следует считать .

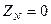Воздушные линии

Сопротивления нулевой последовательности воздушных линий зависят от числа цепей и наличия защитных тросов.

Ток нулевой последовательности воздушной линии возвращается через землю и по заземленным цепям, расположенным параллельно данной линии (защитные тросы, рельсовые пути вдоль линии, трасса газопровода вдоль линии и др.).

Достоверное определение сопротивления нулевой последовательности воздушной линии связано с учетом распределения тока в земле, точно нахождение которого представляет сложную задачу.

В табл. 4.2 приведены средние значения соотношений между 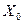и 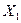для воздушных линий передачи.

Таблица 4.2

Характеристика воздушной линии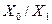
Одноцепная без тросов	3,5
Одноцепная со стальными тросами	3,0
Одноцепная с хорошо проводящми тросами	2,0
Двухцепная без тросов	5,5
Двухцепная со стальными тросами	4,7
Двухцепная с хорошо проводящими тросами	3,0

Кабели

Значения 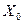кабелей обычно находят по заводским данным, приводимым в справочной литературе.

Для кабелей в зависимости от пути тока нулевой последовательности (только по оболочке или по оболочке и в земле) сопротивление нулевой последовательности ориентировочно находится в пределах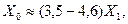

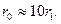
4.4. Порядок составления схем замещения отдельных последовательностей

4.4.1 Общие замечания

При использовании метода симметричных составляющих к расчету любого несимметричного режима одной из первоочередных задач является составление схем замещения в общем случае всех трех последовательностей (прямой, обратной и нулевой).

При аналитическом решении поставленной задачи по этим схемам находят результирующие сопротивления отдельных последовательностей рассматриваемой системы относительно места, где возникла несимметрия. Из схемы замещения прямой последовательности, помимо того, определяют результирующую э.д.с. относительно той же точки.

Схемы замещения отдельных последовательностей составляют в соответствии с указаниями § 2.2.4.

В частности, сопротивления и э.д.с. элементов схем замещения выражают в именованных или относительных единицах, приводя их соответственно к выбранной основной ступени напряжения или к выбранным базисным условиям.

4.4.2. Порядок сставления схем замещения

прямой и обратной последовательностей

Схема замещения прямой последовательности является обычной схемой, которую составляют для расчета любого симметричного трехфазного режима.

В зависимости от применяемого метода расчета и рассматриваемого момента времени в нее вводят генераторы и нагрузки соответствующими реактивностями и э.д.с. Все остальные элементы вводят в схему замещения неизменными сопротивлениями.

Поскольку пути циркуляции токов обратной последовательности те же, что и токов прямой последовательности, схема замещения обратной последовательности по структуре аналогична схеме прямой последовательности.

Различие между ними состоит прежде всего в том, что в схеме обратной последовательности э.д.с. всех генераторных ветвей условно приинимают равными нулю (см.§ 4.3) и кроме того, считают, что реактивности обратной последовательности электрических машин и обобщенных нагрузок постоянны и не зависят от вида и условий возникшей несимметрии, а также от рассматриваемого момента времени.

Началом схемы прямой и обратной последовательностей считают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей. Это точка нулевого потенциала схемы соответствующей последовательности.

Концом схемы прямой или обратной последовательностей считают точку, где возникла рассматриваемая несимметрия.

При продольной несимметрии каждая из схем имеет два конца; ими яв-

ляются две точки, между которыми расположена данная продольная несим-

метрия.

К концу или между концами схем отдельных последовательностей приложены напряжения соответствующих последовательностей, возникающие в месте несимметрии.

4.4.3.Порядок составления схемы замещения нулевой последовательности

Токи нулевой последовательности по существу являются однофазным током, разветвленным между тремя фазами (векторы токов нулевой последовательности имеют одинаковое направление во всех фазах) и воз-

вращающимся через землю и параллельные ей цепи.

В этой связи, путь циркуляции токов нулевой последовательности резко отличается от пути, по которому проходят токи прямой и обратной последовательностей.

Конфигурация схемы замещения нулевой последовательности в значительной мере определяется видом соединений обмоток трансформа-торов и автотрансформаторов.

Составление схемы замещения нулевой последовательности следует начинать от точки где возникла несимметрия, считая, что в этой точке все фазы замкнуты между собой накоротко и к ней приложено напряжение ну-

левой последовательности. В зависимости от вида несимметрии это напря-

жение прикладывается или относительно земли (поперечная несимметрия, рис.4.3, ) или последовательно в рассечку фазных проводов (продольная несимметрия, рис. 4.3, ).

Исходя из соответствующего данной несимметрии включения напряжения нулевой поледовательности, следует выявить в пределах каждой электрически связанной цепи возможные пути протекания токов нулевой последователь-

ности.

Следует иметь ввиду, что если напряжение нулевой после- довательности приложено относительно земли, то при от- …Рис.4.3. сутствии емкостной проводимости для циркуляции токов нулевой последовательности необходима по меньшей мере одна заземлен-

ная нейтраль в той же электрически связанной цепи, где приложено это напряжение.

При наличии нескольких заземленных нейтралей в этой цепи образуются соответственно несколько параллельных контуров для токов нулевой последовательности.

При продольной несимметрии (напряжение нулевой последовательности введено последовательно в рассечку фазных проводов) циркуляция токов нулевой последовательности возможна даже при отсутствии заземленных нейтралей, если при этом имеется замкнутый контур через обходные пути той же электрически связанной цепи (при этом в земле циркулирует наведенный ток, следуя по трассе линии).

При отсутствии таких путей протекание токов нулевой последовательно-

сти в рассматриваемых условиях возможно только в том случае, если в той же электрически связанной цепи имеются заземленные нейтрали с обеих сторон от места, где приложено напряжение нулевой последовательности.

Сопротивление, через которое заземлена нейтраль трансформатора, генератора, двигателя или нагрузки, должно быть введено в схему нулевой последовательности утроенной величиной.

Это обусловлено тем, что любую схему замещения составляют для одной фазы, а через сопротивление, включенное в нейтраль протекает сумма токов нулевой последовательности всех трех фаз.

На рис.4.4 показан пример составления схемы замещения нулевой после-

довательности для случая, когда напряжение нулевой последовательности возникает между проводами фаз и землей (поперечная несимметрия).

Обмотки трансформаторов, автотрансформатора и прочие элементы схемы рис.4.4 обозначены порядковыми номерами, которые сохранены в обозначениях элементов схемы нулевой последовательности.

Поскольку в цепи среднего напряжения автотрансформатора имеется путь для токов нулевой последовательности, автотрансформатор входит

своей полной схемой замещения. Циркуляция тока нулевой последователь-

ности в обмотке 12 трансформатора Т-2 обеспечена через заземленную ней-

траль нагрузки. Этот трансформатор предполагается трехстержневым и по-

этому учтена его реактивность намагничивания нулевой последовательно-

сти.

Для другого трансформатора и автотрансформатора указания об их кон-

струкции практически не нужны, так как они имеют обмотки, соединенные треугольником.

Если предположить, что в той же точке напряжение нулевой последова-

тельности приложено в рассечку фазных проводов, то легко убедиться в том, что в этом случае схема замещения нулевой последовательности оста-

нется прежней, но ее результирующее сопротивление будет совсем иным.

Рис.4.4.

а – расчетная схема; б – схема замещения нулевой последовательности

4.4.4. Порядок определения результирующих э.д.с. и сопротивления

Следующий этап аналитического расчета несимметричного режима заключается в определении результирующих сопротивлений схем замеще-

ния отдельных последовательностей относительно точки, где возникла не-

симметрия. Кроме этого, на этом этапе из схемы прямой последовательнос-

ти находят также результирующую э.д.с. относительно той же точки.

При этом нужно иметь в виду принципиальное различие в преобразова-

нии схем замещения при поперечной и продольной несимметриях.

Обратимся к конкретной расчетной схеме рис.4.5, и проследим на ней за тем, в чем именно состоит это различие.

На расчетной схеме и в схемах замещения отдельных последовательнос-

тей ( рис.4.5, 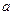, , 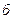, , 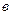, , 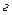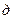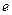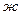) все элементы и сопротивления пронумерова-

ны.

При поперечной несимметрии в точке 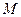схема замещения прямой после-

довательности имеет вид, представленный на рис.4.5, 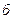. Последовательно соединенные в ней сопротивления 1 и 2, а также 5 и 6 обозначены соответ-

ственно номерами 8 и 9.

Для определения результирующих э.д.с. и сопротивления относительно точки 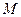достаточно заменить ветвь 9 с 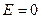и ветвь, получаемую сложени-

ем сопротивления 8 с параллельно соединеннными сопротивлениями 3 и 4 и имеющуюся э.д.с. 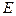, одной эквивалентной (рис.4.5, ).

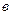Схема замещения обратной последовательности и ее преобразования аналогичны, за исключением того, что в ней отсутствуют э.д.с. источников.

Рис.4.5.

Схему замещения нулевой последовательности (рис.4.5, 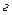) также легко преобразовать к результирующему сопротивлению относительно точки 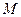путем последовательного и параллельного сложения ветвей.

Пусть теперь в точке 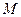возникла продольная несимметрия.

В этом случае напряжение прямой последовательности в точке 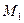должно быть введено в рассечку цепи сопротивления 4 (рис.4.5, ).

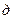Для определения результирующих э.д.с. и сопротивления схемы относи-

тельно точки 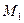в данном случае необходимо вначале сложить последова-

тельно сопротивления 8 и 9. Затем образовавшуюся ветвь 10 с э.д.с. 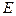и ветвь 3 (рис.4.5, 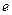) следует заменить эквивалентной, что дает искомую результирующую э.д.с. относительно точки 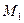, а для нахождения результи-