А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 7 страница
рующего сопротивления относительно той же точки достаточно к сопротив-
лению полученной эквивалентной ветви прибавить сопротивление 4.
Схема замещения обратной последовательности аналогична схеме рис.4.5, 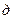 ; в ней лишь отсутствует э.д.с. источника. Ее результирующее сопротивление относительно точки
; в ней лишь отсутствует э.д.с. источника. Ее результирующее сопротивление относительно точки 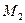 находится также как и схемы замещения прямой последовательности.
находится также как и схемы замещения прямой последовательности.
В схему замещения нулевой последовательности (рис.4.5, 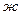 ) двухцепная линия введена своей трехлучевой схемой замещения с сопротивлениями 11, 12 и 13 (см. Приложение П-8 [4]) c тем, чтобы учесть взаимоиндукцию между цепями, находящимися теперь в различных условиях.
) двухцепная линия введена своей трехлучевой схемой замещения с сопротивлениями 11, 12 и 13 (см. Приложение П-8 [4]) c тем, чтобы учесть взаимоиндукцию между цепями, находящимися теперь в различных условиях.
Для определения результирующего сопротивления схемы относительно точки 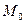 нужно сопротивление 11 сложить параллельно с суммой сопротивлений 2, 13, 5 и 7 (сопротивление 7 входит утроенной величиной) и затем прибавить сопротивление 12.
нужно сопротивление 11 сложить параллельно с суммой сопротивлений 2, 13, 5 и 7 (сопротивление 7 входит утроенной величиной) и затем прибавить сопротивление 12.
4.5. Учет влияния трансформации на распределение токов и напряжений
Фазные токи и напряжения при несимметричных режимах проще всего находить путем суммирования их симметричных составляющих.
Поскольку рассматриваемые трехфазные схемы предполагаются выполненными симметрично, то распределение токов и напряжений каждой последовательности находят в схеме замещения одноименной последовательности, руководствуясь правилами и законами распределения токов и напряжений в линейных электрических цепях[1].
При определении фазных величин за трансформаторами нужно иметь в виду, что векторы токов и напряжений при переходе через трансформатор изменяются не только по величине, но и по фазе в зависимости от вида соединения его обмоток.
Обратимся к рис.4.6, где приведена принципиальная схема траносформатора с соединением обмоток звезда с заземленной нейтралью/треугольник.
 |
Если число витков фазных обмоток соответственно равны
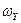 и
и 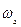 , то линейный коэффициент трансформации будет
, то линейный коэффициент трансформации будет 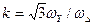 .
.
Рис.4.6.
При заданных фазных токах 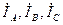 звезды и в соответствии с принятыми на рис. 4.6 положительными направлениями для токов в линейных проводах за треугольником имеем:
звезды и в соответствии с принятыми на рис. 4.6 положительными направлениями для токов в линейных проводах за треугольником имеем:
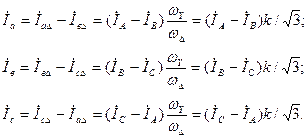 (4.13)
(4.13)
Эту запись можно видоизменить, выразив токи через их симметричные составляющие.
Так, например для тока 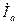 получим
получим
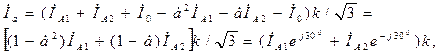 (4.14)
(4.14)
откуда, в частности, видно, что линейные токи на стороне обмотки трансформатора, соединенной в треугольник, не содержат составляющих нулевой последовательсти.
Аналогично могут быть найдены напряжения на стороне обмотки трансформатора, соединенной в треугольник.
Если 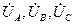 - фазные напряжения со стороны звезды, включающие в себя и падения напряжения в самом трансформаторе, то искомые фазные напряжения со стороны треугольника будут:
- фазные напряжения со стороны звезды, включающие в себя и падения напряжения в самом трансформаторе, то искомые фазные напряжения со стороны треугольника будут:
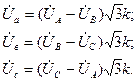 (4.15)
(4.15)
При выражении напряжений через симметричные составляющие, напрмер, для напряжения 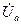 , будем иметь:
, будем иметь:

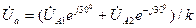 . (4.16)
. (4.16)
Структура выражений (4.14) и (4.16) показывает, что при переходе со стороны звезды на сторону треугольника трансформатора, обмотки которого соединены по группе 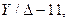 векторы прямой последовательности повертываются на
векторы прямой последовательности повертываются на 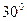 в направлении вращения векторов (против направления движения стрелки часов), а векторы обратной последовательности – на
в направлении вращения векторов (против направления движения стрелки часов), а векторы обратной последовательности – на 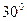
в противоположном направлении (рис.4.7-4.8).
При переходе через трансформатор в обратном направлении угловые смещения симметричных составляющих меняют свой знак на противоположный.

Рис.4.7. Рис.4.8.
4.6. Анализ отдельных видов несимметричных коротких замыканий
4.6.1. Двухфазное короткое замыкание
Для наглядности и удобства рассуждений короткие замыкания будут рассматриваться на отпайках, отходящих от фазных проводов, причем сопротивления проводов отпаек принимаются равными нулю (рис.4.9).
При двухфазном к.з. токи нулевой последовательности отсутствуют и поэтому для его анализа достаточно иметь только две схемы замещения: прямой и обратной последовательностей.
Предположим, что эти схемы замещения уже составлены, приведены к простейшему виду и известны их результирующие 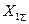 и
и 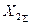 , а также
, а также 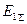 .
.
 |
Для дальнейших рассуждений воспользуемся схемой рис. 4.10.
Рис.4.9. Рис.4.10.
Уравнения (4.8)-(4.9) дают лишь две связи между четырьмя неизвестными, поэтому для их решения нужны еще два уравнения, которые получают из граничных условий для двухфазного к.з.:
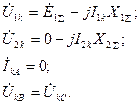 (4.17)
(4.17)
Система уравнений составлена для фазы  , но она имеет силу для любой другой фазы.
, но она имеет силу для любой другой фазы.
При записи граничных условий для всех видов несимметрии принимают, что фаза  находится в условиях отличных от условий для двух других фаз, то есть она является, как говорят, особой фазой.
находится в условиях отличных от условий для двух других фаз, то есть она является, как говорят, особой фазой.
За положительное направление фазных токов и их симметричных составляющих принимают направление к месту короткого замыкания.
В дальнейшем условимся при записи симметричных составляющих фазы  не указывать индекс фазы.
не указывать индекс фазы.
Согласно системе уравнений (4.2) 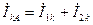 , но из (4.17)
, но из (4.17) 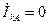 ,
,
следовательно, 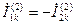 . (4.18)
. (4.18)
Согласно (4.3)-(4.5)
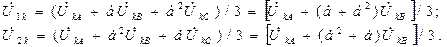 (4.19)
(4.19)
Используя (4.17)-(4.19), можно записать:
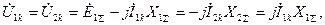
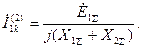 (4.20)
(4.20)
Согласно (4.2) токи в фазах будут:
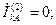
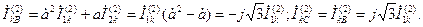 (4.21)
(4.21)
Симметричные составляющие напряжения для фазы  при двухфазном к.з. определим согласно формул (4.17)-(4.19):
при двухфазном к.з. определим согласно формул (4.17)-(4.19):
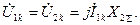
Тогда в соответствии с (4.2) напряжения фаз будут:
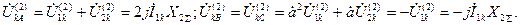 (4.22)
(4.22)
Заметим, что напряжение неповрежденной фазы в два раза больше по модулю напряжения поврежденных фаз и противоположно по знаку.

На рис. 4.11 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при двухфазном к.з. в точке К.
Рис.4.11.
а – векторная диаграмма токов;
б – векторная диаграмма напряжений;
в – комплексная cхема замещения
Комплексная схема замещения предназначена для расчетов несиметричных режимов на расчетных столах переменного и постоянного тока.
Конфигурация комплексной схемы замещения определяется по выражению для тока прямой последовательности для рассматриваемого вида несимметрии.
Условные обозначения на комплексной схеме замещения : 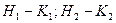 и т.д. служат для фиксации начала (
и т.д. служат для фиксации начала ( 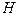 ) и конца набранной на расчетном столе схемы замещения соответствующей последовательности.
) и конца набранной на расчетном столе схемы замещения соответствующей последовательности.
По измерениям, проводимым на комлексной схеме замещения, набранной на расчетном столе постоянного тока, можно определить модули токов и напряжений всех последовательностей для фазы  .
.
Зная из анализа каждого вида несимметрии положение векторов токов и напряжений всех последовательностей для фазы  на соответствующих векторных диаграммах, далее строят системы векторов симметричных составляющих токов и напряжений для всех фаз и получают по ним искомые векторы полных фазных величин.
на соответствующих векторных диаграммах, далее строят системы векторов симметричных составляющих токов и напряжений для всех фаз и получают по ним искомые векторы полных фазных величин.
Так, для рассматриваемого вида несимметричного к.з. достаточно применить в комлексной схеме замещения только два измерительных прибора: амперметр, включаемый в разрыв последовательной цепи и вольтметр, подключаемый к точкам 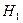 и
и 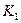 .
.
При этом, первый прибор покажет значение модуля тока прямой последовательности фазы  , второй – модуля напряжения прямой последовательности фазы
, второй – модуля напряжения прямой последовательности фазы  .
.
Таким образом, ценность применения комплексных схем замещения состоит в простоте определения искомых фазных величин в любой точке длясети любой сложности, схемы замещения соответствующих последовательностей которой набраны и соединены между собой соответствующим образом на расчетном столе.
4.6.2. Однофазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.12) нужно иметь три схемы замещения –
прямой обратной и нулевой последовательностей.
 Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны
Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны 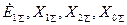 .
.
Для этого случая к.з. с учетом граничных условий можно записать следующие уравнения
Рис.4.12.
 |
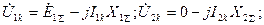
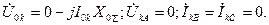 (4.23) Согласно (4.3)-(4.5) и (4.23) имеем:
(4.23) Согласно (4.3)-(4.5) и (4.23) имеем:

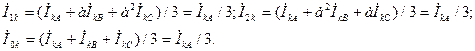
Следовательно, 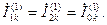 (4.24)
(4.24)
Согласно (4.2) и (4.23) имеем: 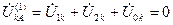 , а используя (4.24), получим:
, а используя (4.24), получим: 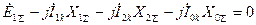 .
.
Таким образом, 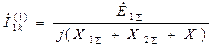 . (4.25)
. (4.25)
Токи в фазах согласно (4.23)-(4.24) будут:
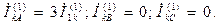 (4.26)
(4.26)
Ток в земле будет равен:
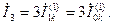 (4.27)
(4.27)
Напряжения фаз
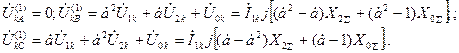 (4.28)
(4.28)
На рис. 4.13 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при однофазном коротком замыкании на землю в точке  .
.
Векторная диаграмма токов строится на основании формулы (4.24), а напряжений – исходя из того, что 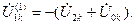

Угол 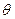 между векторами
между векторами 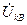 и
и 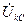 изменяется от 60 до
изменяется от 60 до 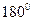 .
.
 |
Рис.4.13.
а - векторная диаграмма токов;
б – векторная диаграмма напряжений;
в – комплексная схема замещения
4.6.3. Двухфазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.14) нужно иметь три схемы замещения – прямой обратной и нулевой последовательностей.
Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны 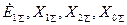 .
.
 Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде:
Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде: 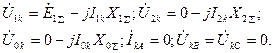 (4.29) Согласно (4.3)-(4.5) и (4.29) имеем:
(4.29) Согласно (4.3)-(4.5) и (4.29) имеем:
Рис.4.14. 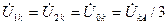 . (4.30)
. (4.30)
Из (4.29) следует, что:
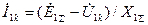 ;
; 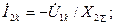
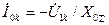 .
.
Так как 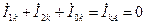 ,
,
то 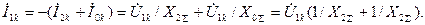
Подставляя выражение для 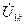 из последнего выражения в (4.29), получим
из последнего выражения в (4.29), получим 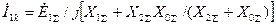 ;
; 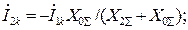

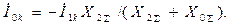 (4.31)
(4.31)
Токи в фазах при двухфазном к.з.на землю будут:
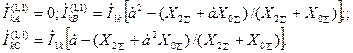 . (4.32)
. (4.32)
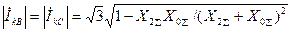 . (4.33)
. (4.33)
Ток в земле при двухфазном к.з. на землю
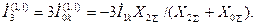 (4.34)
(4.34)
Напряжения фаз
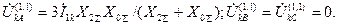 (4.35)
(4.35)
 |
На рис. 4.15 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при двухфазном коротком замыкании на землю в точке К.
Рис.4.15.
а – векторная диаграмма токов;
б – векторнафя диаграмма напряжений;
в – комплексная схема замещения
4.7. Обобщение результатов
анализа отдельных видов несимметричных коротких замыканий
Если рассмотреть формулы (4.20), (4.25) и (4.32), приняв во внимание только модуль значения составляющей тока прямой последовательности, то можно видеть:
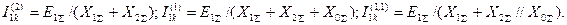 (4.36)
(4.36)
Как следует из (4.36), для каждого из значений тока прямой последова-
тельности структурно можно записать выражение:
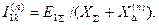 (4.37)
(4.37)
Выражение (4.37) позволило Н.Н.Щедрину сделать обобщение [5]:
“Ток прямой последовательности при любом несимметричном к.з. может быть определен как ток трехфазного к.з. в точке, удаленной от действи-
тельной точки к.з. на дополнительную реактивность 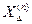 , которая не за-
, которая не за-
висит от параметров схемы прямой последовательности и для каждого вида к.з. в рассматриваемой точке остается неизменной для всего процес-
са к.з.”
Из формул (4.21), (4.26) и (4.2) модули значений токов в поврежденных фазах будут равны:
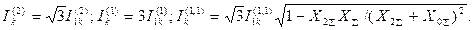 (4.38)
(4.38)
Из (4.38) следует, что структурно общей формулой для токов в повреж-
денных фазах при любом виде к.з. может служить выражение:
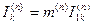 . (4.39)
. (4.39)
Исходя из выражений (4.37) и (4.39) для определения токов в поврежденных фазах при различных видах к.з., нужно использовать данные, приведенные в табл.4.3.
Таблица 4.3
Значения дополнительной реактивности 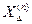 и множителя
и множителя 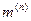
| Вид короткого замыкания | 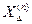
| 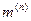
|
| Трехфазное | ||
| Двухфазное | 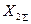
| 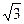
|
| Однофазное на землю | 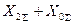
| |
| Двухфазное на землю | 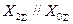
| 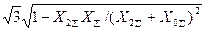
|
Как следует из (4.37)-(4.38), для вычисления несимметричных токов к.з. можно использовать все приемы, применяемые при расчете тока трехфазно-
го к.з.
Например, при расчете несимметричного к.з. по расчетным кривым при-
меняют те же расчетные кривые, по которым рассчитывают ток трехфазно-
го к.з.
При этом расчетная реактивность 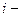 той независимой генерирующей ветви источника при использовании расчетных кривых для определения тока несимметричного к.з. рассчитывается по формуле:
той независимой генерирующей ветви источника при использовании расчетных кривых для определения тока несимметричного к.з. рассчитывается по формуле:
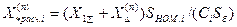 . (4.40)
. (4.40)
Следует иметь в виду, что при использовании приемов расчета тока трехфазного к.з. для расчета тока несимметричного к.з. вида 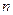 определяется только ток прямой последовательности
определяется только ток прямой последовательности 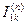 .
.
Так, например, по расчетным кривым находится только ток прямой последовательности 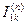 .Чтобы найти токи в поврежденных фазах при несимметричном к.з. вида
.Чтобы найти токи в поврежденных фазах при несимметричном к.з. вида 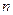 , нужно найденный по расчетным кривым ток прямой последовательности
, нужно найденный по расчетным кривым ток прямой последовательности 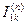 умножить на множитель
умножить на множитель 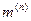 .
.
4.8. Учет переходного сопротивления в месте замыкания
Известно, что электрическую дугу на открытом воздухе в первом приближении можно характеризовать активным сопротивлением 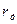 .
.
Рассмотрим пути учета сопротивления дуги при различных видах несимметричных к.з.
Дата добавления: 2016-04-14; просмотров: 872;
