Двухфазное замыкание на землю через дугу

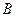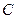При к.з. между фазами и с одновременным замыканием той же точки наземлю через сопротивление дуги 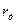(рис.4.16, 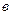), последнее, очевидно, войдет только в схему нулевой последоватеьности, причем войдет своей утроенной величиной.

Поэтому выражение для тока прямой последовательности в месте замыкания по аналогии с (4.31) будет:

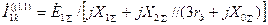; (4.46)

соответственно для напряжения прямой последовательносмти за сопротивлением 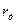(точка ):

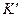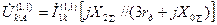. (4.47)

Для определения токов обратной и нулевой последовательностей в месте замыкания служат соответственно выражения (4.31), в которых вместо 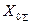следует ввести .

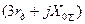Поскольку фазы 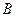и 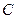замкнуты между собой накоротко, то независимо от величины 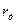соотношение (4.20) сохраняется, то есть напряжение обратной последовательности за сопротивлением 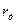следует определять по (4.47).

Что касается напряжения нулевой последовательности в точке 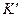, то оно, очевидно, равно падению напряжения от тока 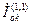в .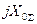

В табл.4.4 приведены установленные выше соотношения для симметричных составляющих токов и напряжений в месте несимметричных замыканий через дугу сопротивлением 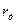, а в табл.4.5 приведены выражения для дополнительного сопротивления 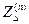и коэффициента .

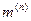Таблица 4.4