Симметричные составляющие токов и напряжений
| Определяемые величины и их обозначения | При замыканиях | |||
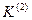
| 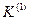
| 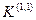
| ||
| Ток прямой последовательности | 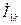
| 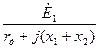
| 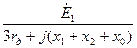
| 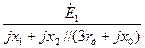
|
| Ток обратной последовательности | 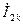
| 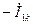
| 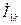
| 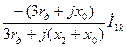
|
| Ток нулевой последовательности | 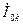
| 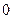
| 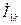
| 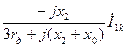
|
| Напряжение прямой последовательности | 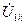
| 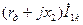
| 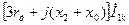
| 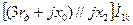
|
| Напряжение обратной последовательности | 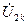
| 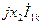
| 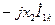
| 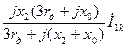
|
| Напряжение нулевой последовательности | 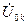
| Предшествующее значение | 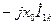
| 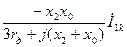
|
Таблица 4.5
Значения дополнительного сопротивления 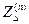 и коэффициента
и коэффициента 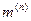
| Вид замыкания | 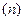
| 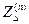
| 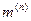
|
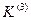
| (3) | ||
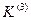
| (2) | 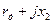
| 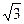
|
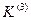
| (1) | 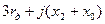
| |
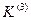
| (1,1) | 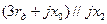
| 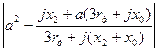
|
То же при 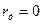
| (1,1) | 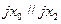
| 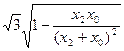
|
Примечание.В таблицах 4.4 и 4.5 для упрощения записи опущен индекс “ 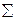 ” у
” у 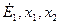 и
и 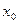 , которые являются сооответствующими результирующими величинами относительно места замыкания.
, которые являются сооответствующими результирующими величинами относительно места замыкания.
4.9. Сравнение отдельных видов короткого замыкания
Правило эквивалентности прямой последовательности и установленные значения 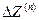 и
и 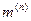 позволяют достаточно просто произвести сравнение различных видов к.з.
позволяют достаточно просто произвести сравнение различных видов к.з.
Рассмотрим это при условии, когда цепь к.з. чисто индуктивная.
Имея в виду, что короткие замыкания разных видов предполагаются происходящими поочередно в одной и той же точке системы и при одних и тех же исходных условиях, на основании данных табл.4.3, 4.4 и 4.5 можно написать, что между величинами дополнительных реактивностей 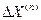 при разных видах к.з. существуют следующие неравенства:
при разных видах к.з. существуют следующие неравенства:
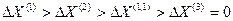 ; (4.48)
; (4.48)
соответственно 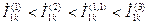 (4.49)
(4.49)
и 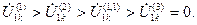 (4.50)
(4.50)
Выясним примерные пределы, в которых могут находиться величины токов при несимметричных к.з. пр сравнению с величинами токов трехфазного к.з., возникающего в той же точке системы.
При этом абсолютную величину отношения тока в месте любого несимметричного металлического к.з. вида ( 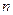 ) можно представить как
) можно представить как
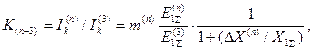 (4.51)
(4.51)
где у результирующей э.д.с. поставлен индекс , указывающий какому виду к.з. соответствует ее значение.
Выражение (4.51) справедливо для произвольного момента времени; при этом в зависимости от того, какой реактивностью введен генератор в схему прямой последовательности, для него должна быть принята соответствующая э.д.с.
Для приближенной оценки пределов изменения 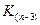 можно пренебречь различием величин
можно пренебречь различием величин 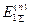 и
и 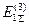 .
.
Тогда для начального момента к.з. имеем 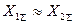 , а для установившегося режима
, а для установившегося режима 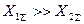 .
.
Следовательно, отношение 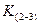 будет находится примерно в следующих пределах:
будет находится примерно в следующих пределах: 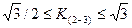 . (4.52)
. (4.52)
При достаточно большой удаленности к.з. токи двухфазного и трехфазного к.з. изменяются мало во времени, благодаря чему между ними в течение всего процееса к.з. сохраняется приблизительно постоянное соотношение 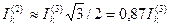 . (4.53)
. (4.53)
Поскольку реактивность 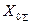 может изменяться в очень широких пределах (почти от 0 до
может изменяться в очень широких пределах (почти от 0 до 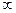 ), то отношение
), то отношение 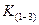 находится в диапазоне
находится в диапазоне
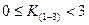 .
.
 |
При к.з. в точках системы, где
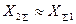 , отношение
, отношение 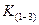 , находясь в пределах
, находясь в пределах 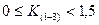 , изменяется в функции отношения
, изменяется в функции отношения 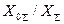 , как показано на рис.4.17.
, как показано на рис.4.17.
Рис.4.17.
Пределы отношения 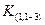 получаются те же, что и для
получаются те же, что и для 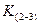 .
.
Изменение отношения 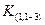 в зависимости от
в зависимости от 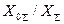 при
при 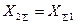 характеризует соответствующая кривая на рис.4.17.
характеризует соответствующая кривая на рис.4.17.
Как видно, в диапазоне 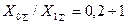 ток однофазного к.з. немного больше тока двухфазного к.з на землю, в то время как при всех остальных значениях
ток однофазного к.з. немного больше тока двухфазного к.з на землю, в то время как при всех остальных значениях 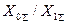 имеет место обратное соотношение, которое прогрессивно увеличивается с ростом
имеет место обратное соотношение, которое прогрессивно увеличивается с ростом 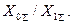
Практически интерес представляет также сравнение величин токов в земле при однофазном и двухфазном к.з. на землю.
Используя (4.24), (4.25) и (4.31), находим, что отношение 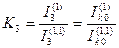 можно представить в следующем виде
можно представить в следующем виде
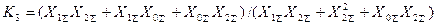 ,
,
откуда следует, что в зависимости от соотношения между 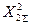 и
и 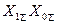 может быть
может быть 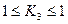 .
.
При 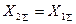 выражение (4.54) принимает более простой вид:
выражение (4.54) принимает более простой вид:
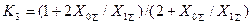
и в данном случае пределы 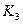 будут:
будут:
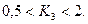
Изменение 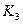 в функции
в функции 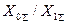 иллюстрирует соответствующая кривая рис. 4.17.
иллюстрирует соответствующая кривая рис. 4.17.
Как видно, лишь при 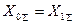 токи в земле при сравниваемых видах к.з. одинаковы; при
токи в земле при сравниваемых видах к.з. одинаковы; при 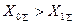 ток в земле больше при однофазном к.з., а при
ток в земле больше при однофазном к.з., а при 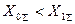 , напротив, больше ток при двухфазном к.з. на землю.
, напротив, больше ток при двухфазном к.з. на землю.
Соотношения (4.54),(4.55) справедливы для токов нулевой последовательности любой ветви схемы, так как они пропорциональны токам в месте к.з.
4.10. Анализ однократной продольной несимметрии
4.10.1. Общие замечания
Продольную несимметрию в какой -либо точке трехфазной сети в общем виде можно представить включением в рассечку каждой фазы неодинако-
вых сопротивлений.
Такой подход универсален, так как позволяет получить расчетные выражения в самом общем виде.
Однако указанный прием связан с необходимостью проведения сложных выкладок, а сам конечный результат характеризуется громоздкими выраже-
ниями.
Значительно проще и нагляднее проводить решение для каждого вида про- дольной несимметрии, используя характеризующие его граничные условия.
В данном параграфе будут рассмотрены два вида наиболее часто встречающейся продольной несимметрии, а именно: разрыв одной фазы и разрыв двух фаз (в одном и том же месте).
Основные уравнения падений напряжения в схемах замещения каждой последовательности, составленные для симметричной части сети, аналогичны уравнениям (4.3)-(4.5), и при чисто индуктивной цепи их можно представить в виде:
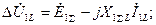 (4.54)
(4.54)
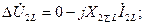 (4.55)
(4.55)
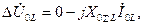 (4.56)
(4.56)
где 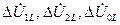 - симметричные составляющие падения напряжения фазы
- симметричные составляющие падения напряжения фазы  на несимметричном участке сети;
на несимметричном участке сети;
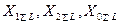 - результирующие реактивности схем замещения соответст-
- результирующие реактивности схем замещения соответст-
вующих последовательностей относительно места продольной несиммет-
рии. 
Дополнительные связи между симметричными составляющими токов и напряжений устанавливаются из граничных условий рассматриваемой продольной несимметрии.
4.10.2. Разрыв одной фазы
Разрыв одной фазы (рис.4.17) можно характеризовать следующми граничными условиями:
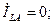 (4.57)
(4.57)
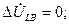 (4.58)
(4.58)
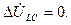 (4.59)
(4.59)
Эти условия аналогичны граничным условиям двухфазного к.з. на землю, следовательно данная аналогия должна быть и в расчетных выражениях.
 Так при разложении на симметричные составляю-
Так при разложении на симметричные составляю-
щие условия (4.58)-(4.59) приводят к равенствам:
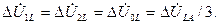 (4.60)
(4.60)
Используя (4.55)-(4.56) и (4.60), выразим 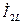 и
и 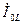 через
через 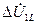 :
:
Рис.4.17. 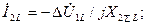 (4.61)
(4.61)
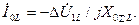 (4.62)
(4.62)
В соответствии с (4.57) можно записать
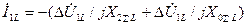 ,
,
откуда 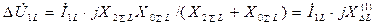 , (4.63)
, (4.63)
где верхний индекс (1) и далее (2) одновременно с нижним индексом 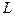 указывает обрыв соответственно одной и двух фаз.
указывает обрыв соответственно одной и двух фаз.
После подстановки (4.63) в (4.54), получим:
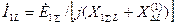 . (4.64)
. (4.64)
Подставляя (4.63) в (4.61)-(4.62), найдем:
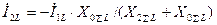 ; (4.65)
; (4.65)
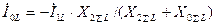 . (4.66)
. (4.66)
Для определения напряжений с одной из сторон продольной несииметрии
(при разрыве одной фазы) нужно предварительно найти по схемам отдель-
ных последовательностей симметричной части цепи соответствующие со-
ставляющие этих напряжений. Прибавив к ним 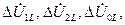 получают симметричные составляющие напряжений с другой стороны продольной несимметрии.
получают симметричные составляющие напряжений с другой стороны продольной несимметрии.
Далее, зная все симметричные составляющие токов и напряжений, определяют фазные величины токов и напряжений путем сложения симметричных составляющих соответствующих фаз.
В частности, для определения фазных токов в месте обрыва одной фазы могут быть использованы выражения, аналогичные (4.32), в которых ток 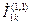 и реактивности
и реактивности 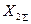 и
и 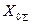 должны быть соответственно замененены током
должны быть соответственно замененены током 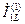 и реактивностями
и реактивностями 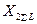 и
и 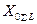 .
.
Аналогично, для нахождения модуля фазных токов при обрыве одной фазы может быть использован коэффициент, определяемый по выражению, аналогичному (4.33).
 |
На рис. 4.18 в качестве иллюстрации приведены векторные диаграммы напряжений по концам разрыва (соответственно в точках
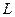 и
и 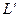 ), а на рис.4.19 – комплексная схема замещения.
), а на рис.4.19 – комплексная схема замещения.
 |
Рис.4.18.
Рис.4.19.
4.10.3. Разрыв двух фаз
При разрыве двух фаз (рис.4.20) граничные условия, очевидно будут:
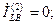 (4.67)
(4.67)

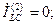 (4.68)
(4.68)
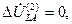 (4.69)
(4.69)
то есть они аналогичны граничным условиям однофазного к.з.В соответствии с (4.23)-(4.24) следует, что симметричные составляющие тока фазы  в месте обрыва двух других фаз связаны соотношением:
в месте обрыва двух других фаз связаны соотношением:
Рис.4.20. 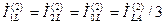 . (4.70) С другой стороны, поскольку согласно (4.69)
. (4.70) С другой стороны, поскольку согласно (4.69)

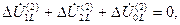 (4.71)
(4.71)
достаточно сложить правые части уравнений (4.54)-(4.55) и сумму приравнять нулю. Далее, учитывая (4.70), получим:
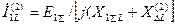 , (4.72)
, (4.72)
где 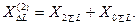 (4.73)
(4.73)
Для фазного тока целой фазы (фаза  ) согласно (4.70) имеем:
) согласно (4.70) имеем:
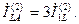 (4.74)
(4.74)
Симметричные составляющие разности фазных напряжений в месте обрыва двух фаз определяются для обратной последовательности соответственно по (4.55) и (4.56), а для прямой последовательности проще по (4.71):
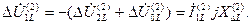 (4.75)
(4.75)
5. ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ
ПРИ ОСОБЫХ УСЛОВИЯХ
5.1. Общие замечания
Распределительные сети напряжением 6-35кВ, питание которых осуществляется от районных подстанций электрической системы, обычно являются второй или третьей ступенью трансформации со стороны генераторов станций системы.
Поэтому одним из характерных признаков таких сетей является их относительно большая электрическая удаленность от источников питания, в силу чего аварийные процессы, возникающие в этих сетях, сравнительно мало сказываются на работе генераторов системы.
Указанное обстоятельство позволяет практически считать, что при любых нарушениях режима работы распределительной сети (6-35 кВ) напряжение высшей ступени трансформации (110 кВ и выше) системы остается неизменным.
В распределительных сетях часто встречаются воздушные и кабельные линии с проводниками сравнительно малых сечений, что приводит к необходимости учета активных сопротивлений таких линий.
При достаточной продолжительности процесса к.з. увеличение активного сопротивления проводника может вызвать заметное снижение тока к.з, которое условно называют тепловым спадом тока к.з.
Распределительные сети 6-35 кВ, как правило, работают с изолированной нейтралью или с нейтралью заземленной через большое сопротивление.
Поэтому при замыкании на землю одной фазы возникающий при этом ток обусловлен только емкостной проводимостью сети и по величине он всегда значительно меньше тока однофазного к.з. в сети с глухо-заземленной нейтралью. Этот вид замыкания на землю называют простым.
Электрические установки напряжением до 1000 В находятся на еще 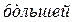 удаленности от генераторов системы, что позволяет с
удаленности от генераторов системы, что позволяет с 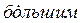 основанием считать напряжение в узле системы, от которого питаются такие установки, неизменным независимо от происходящих в них аварийных процессов.
основанием считать напряжение в узле системы, от которого питаются такие установки, неизменным независимо от происходящих в них аварийных процессов.
5.2. Анализ простого замыкания на землю
Пусть в начале распределительной трехфазной сети 6-35 кВ, присоединенной к источнику переменного тока произошло замыкание на землю фазы  (рис.5.1,
(рис.5.1, 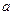 ).
).
 |
Рис.5.1.
Распределенные вдоль линии емкости каждой фазы относительно земли условно представлены сосредоточенными емкостями в конце линии. Частичные емкости между фазами не показаны; при этом отметим, что их влияние на ток замыкания на землю ничтожно.
Проследим путь циркуляции тока замыкания на землю (он указан стрелками). Поступая в землю в месте замыкания, ток возвращается по неповрежденным фазам через их емкостные проводимости относительно земли.
Емкостная проводимость поврежденной фазы  оказывается зашунтированной рассматриваемым замыканием, и ток в этой фазе справа от места замыкания отсутствует, если пренебречь током, который наводится токами двух других фаз на данном участке линии.
оказывается зашунтированной рассматриваемым замыканием, и ток в этой фазе справа от места замыкания отсутствует, если пренебречь током, который наводится токами двух других фаз на данном участке линии.
Характер векторных диаграмм токов слева исправа от места замыкания показан на том же рисунке.
В действительности емкостная проводимость линии распределена равномерно по ее длине, поэтому эпюра пространственного распределения тока нулевой последовательности каждой фазы вдоль линии выражается наклонной прямой (рис.5.1, 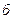 ).
).
Граничные условия для простого замыкания на землю те же, что и для однофазного к.з. 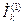 . Поэтому все выражения, полученные выше для
. Поэтому все выражения, полученные выше для 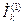 в равной мере относятся к случаю простого замыкания на землю.
в равной мере относятся к случаю простого замыкания на землю.
Емкостные сопротивления элементов распределительной сети 6-35 кВ существенно превышают их индуктивные и активные сопротивления, что позволяет при расчете тока простого замыкания на землю пренебречь индуктивными и активными сопротивлениями и, следовательно, считать, что величина тока простого замыкания на землю практически не зависит от места замыкания.
Приведем в качестве примера значения индуктивных и емкостных сопртивлений для 1 километра воздушной и кабельной линий:
Так, например, провод марки АС-120 при среднегеометрическом расстоянии между проводами фаз 5 м имеет индуктивное сопротивление 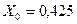 Ом/км и емкостное сопротивление
Ом/км и емкостное сопротивление 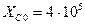 Ом/км; кабель марки АСБ - 3
Ом/км; кабель марки АСБ - 3 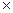 120 напряжением 6 кВ имеет индуктивное сопротивление
120 напряжением 6 кВ имеет индуктивное сопротивление 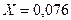 Ом/км и емкостное сопротивление
Ом/км и емкостное сопротивление 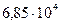 Ом/км.
Ом/км.
Кроме того, так как ток простого замыкания на землю относительно мал (см. величины емкостных сопротивлений), при его определении можно считать, что напряжение источника сохраняется неизменным.
При принятых допущениях ток в месте простого (металлического) замыкания на землю будет:
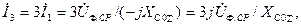 (5.1)
(5.1)
где 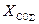 - результирующее емкостное сопротивление нулевой последовательности всех элементов (практически только линий и кабелей), электрически связанных с точкой замыкания;
- результирующее емкостное сопротивление нулевой последовательности всех элементов (практически только линий и кабелей), электрически связанных с точкой замыкания;
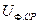 - среднее фазное напряжение той ступени напряжения, где рассматривается простое замыкание на землю.
- среднее фазное напряжение той ступени напряжения, где рассматривается простое замыкание на землю.
Как следует из (5.1) наибольшая величина тока простого замыкания на
землю в три раза превышает емкостной ток на землю одной фазы в нормальных условиях.
Для приближенной оценки порядка величины тока простого замыкания на землю можно использовать соотношение:
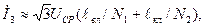 А, (5.2)
А, (5.2)
где 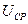 - среднее номинальное напряжение ступени, где рассматривается замыкание, кВ;
- среднее номинальное напряжение ступени, где рассматривается замыкание, кВ;
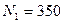 - коэффициент для воздушных линий;
- коэффициент для воздушных линий;
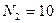 - коэффициент для кабельных линий;
- коэффициент для кабельных линий;
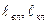 - суммарная длина, соответственно, воздушных и кабельных линий, электрически связанных с точкой простого замыкания на землю, км.
- суммарная длина, соответственно, воздушных и кабельных линий, электрически связанных с точкой простого замыкания на землю, км.
Для симметричных составляющих напряжений при принятых допущениях имеем:
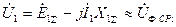 (5.3)
(5.3)
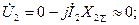 (5.4)
(5.4)
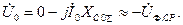 (5.5)
(5.5)
На рис. 5.2. приведены векторные диаграммы токов и напряжений в месте простого металлического замыкания на землю фазы  , которые построены при указанных выше допущениях.
, которые построены при указанных выше допущениях.
Аналогично комплексной схеме при однофазном к.з. на землю может быть составлена такая же схема для случая простого металлического замыкания на землю (см. пример на рис.5.3).
 |
Рис.5.2.
 |
Рис.5.3.
а- исходная схема; б- комплексная схема замещения
Для этого, очевидно, нужно в схеме замещения нулевой последовательности разземлить все нейтрали, а в саму схему нулевой последоватльности ввести еще соответствующие емкостные сопротивления.
Для ограничения тока простого замыкания на землю целесообразно нейтраль трансформатора заземлить через катушку с регулируемой величиной индуктивности (показано пунктиром на рис.5.3).
Индуктивность этой катушки следует выбирать таким образом, чтобы в цепи нулевой последовательности был обеспечен резонанс падений напряжения (на емкости и индуктивности), что приведет к 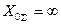 , то есть к отсутствию тока простого замыкания.
, то есть к отсутствию тока простого замыкания.
Пренебрегая индуктивным сопротивлением трансформатора, найдем, что данное условие будет выполнено при 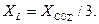
На практике такие катушки называются дугогасящими.
5.3. Методика расчета токов к.з. в установках напряжением до 1000 В
Электрические установки напряжением до 1000 В, питаемые от распределительной сети электрической системы через понижающие трансформаторы, характеризуются , как правило, большой электрической удаленностью относительно источников питания. Это позволяет считать, что при к.з. за таким понижающим трансформатором напряжение в точке сети, где он присоединен, практически остается неизменным и равным своему номинальному значению.
Достоверность расчета токов к.з. в установках напряжением до 1000 В зависит в основном от того, насколько правильно оценены и полно учтены все сопротивления короткозамкнутой цепи.
Наряду с индуктивными сопротивлениями в рассматриваемой ситуации весьма существенную роль играют активные сопротивления таких элементов, как сборные шины и присоединения к ним, тансформаторы тока, контактные сопротивления выключателей, разъединителей, болтовых соединений шин, зажимов и разъемных контактов аппаратов, а также контакта непосредственно в месте к.з. и др., которыми при выполненни аналогичных расчетов для установок высокого напряжения всегда пренебрегают.
Точная оценка сопротивлений контактных соединений представляет трудную задачу, так как эти сопротивления зависят от многих трудноучитываемых факторов(состояния контактных поверхностей, степени затяжки болтов и др.).
С другой стороны, отказ от учета этих сопротивлений приводит к излишнему преувеличению токов к.з. со всеми вытекающими отсюда последствиями, а именно, к применению более мощной аппаратуры и проводников большего сечения, то есть к неоправданным дополнительным затратам на электрооборудование.
В принятых в 1966 г. Указаниях по проектированию силового электрооборудования промышленных предприятий рекомендуется при отсутствиидостоверных данных о переходных сопротивлениях учитывать их совокуп-
но ( включая и контакт в месте к.з.), вводя в короткозамкнутую цепь активное сопротивление, величина которого зависимости от места к.з. оценивается в пределах 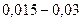 Ом.
Ом.
Нижний предел соответствует к.з. около распределительного щита подстанции, а верхний – при к.з. непосредствено у электроприемников, получающих питание от вторичных распределительных пунктов.
Сопротивления понижающих трансформаторов до 1000 кВА, кабелей до 1000 В, магистральных и распределительных шинопроводов (со спаренными фазами), а также приближенные величины сопротивлений аппаратов напряжений до 1000 В приведены в справочниках.
Сопротивления прямой последовательности шин (обычного исполнения) можно найти в справочниках или определить по выражению
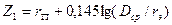 , (5.6)
, (5.6)
где 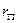 - активное сопротивление фазы;
- активное сопротивление фазы; 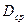 - среднее геометрическое расстояние между шинами фаз
- среднее геометрическое расстояние между шинами фаз 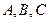 ;
; 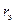 - эквивалентный радиус шины;
- эквивалентный радиус шины;
при этом следует принимать: для круглых шин (радиусом 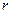 )
) 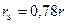 ; для полосовой прямоугольной шины ( с размерами
; для полосовой прямоугольной шины ( с размерами 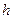 и
и 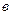 )
) 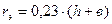 .
.
Для пакета из нескольких полос под 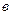 следует понимать толщину пакета в целом.
следует понимать толщину пакета в целом.
Сопротивлеие нулевой последовательности шин зависит от многих факторов (расположения и выполнения заземляющей проводки, близости металлоконструкций и т.д.) и изменяется в широких пределах.
Ориентировочно можно считать, что составляющие этого сопротивления находятся в пределах: 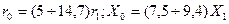 .
.
При составлении схемы замещения следует руководствоваться указаниями § 2.2.
Поскольку сопротивления большинства элементов рассматриваемых установок задаются в именованных единицах, то весь расчет обычно ведут также в именованных единицах; при этом ввиду малых значений самих сопротивлений их выражают в миллиомах ( 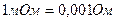 ).
).
Индуктивные сопротивления прямой последовательности воздушных и кабельных линий можно приближенно определить, принимая: 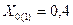 Ом/км
Ом/км 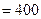 мОм – для воздушных линий;
мОм – для воздушных линий; 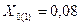 Ом/км=
Ом/км=
=80 мОм – для кабельных линий.
Активное сопротивление воздушных и кабельных линий можно рассчитать по формуле, если известны материал и сечение провода (жилы) фазы: 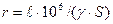 , (5.7)
, (5.7)
где 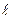 - длина линии, км;
- длина линии, км; 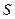 - сечение провода(жилы) фазы,
- сечение провода(жилы) фазы, 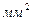 ;
; 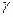 - удельная проводимость проводника,
- удельная проводимость проводника, 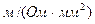 .
.
Относительное активное сопротивление трансфрматора определяют как:
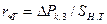 , (5.8)
, (5.8)
где 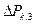 -активные потери мощности короткого замыкания в трансформато-
-активные потери мощности короткого замыкания в трансформато-
ре, кВт; 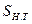 - номинальная мощность трансформатора, кВА.
- номинальная мощность трансформатора, кВА.
Относительное индуктивное сопротивление трансформатора можно определить по формуле:
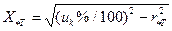 , (5.9)
, (5.9)
где 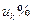 -напряжение короткого замыкания трансформатора, %.
-напряжение короткого замыкания трансформатора, %.
Сопротивления трансформатора в именованных единицах:
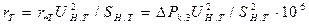 , мОм; (5.10)
, мОм; (5.10)
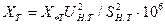 мОм. (5.11)
мОм. (5.11)
В качестве средних номинальных напряжений 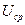 для соответствующих ступеней трансформации рекомендуется принимать: 690, 400, 230 В.
для соответствующих ступеней трансформации рекомендуется принимать: 690, 400, 230 В.
Дата добавления: 2016-04-14; просмотров: 1212;
