Асимметричные алгоритмы шифрования

Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для шифрования данных используется один ключ, а для расшифрования другой (отсюда и название - асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.

Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа шифрования.

Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рисунке 42.

В этой криптосистеме применяют два различных ключа: К_А - открытый ключ отправителя А; К_В - секретный ключ получателя В. Генератор ключа целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ Кв по незащищенному каналу). Значения ключей К_А, К_В – зависят от начального состояния генератора ключей.

Раскрытие секретного ключа К_В по известному ключу К_В должно быть вычислительно неразрешимой задачей.

Характерные особенности асимметричных криптосистем:

1. Открытый ключ Кв и криптограмма С могут быть отправлены по незащищенному каналу, т.е. могут быть известны противнику;

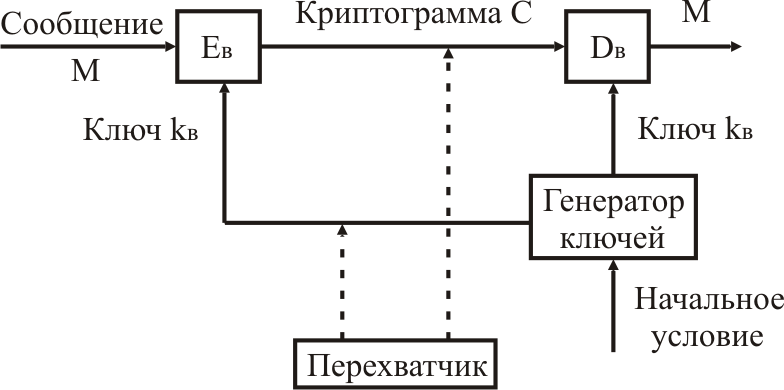Рис. 42. Обобщенная схема асимметричной криптосистемы с открытым ключом

2. Алгоритмы шифрования и расшифрования.

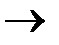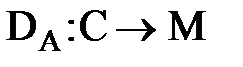Ев: М С, являются открытыми. Защита информации в асимметричной криптосистеме основана на секретности ключа К_В.

У. Диффи и М. Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:

— Вычисление пары ключей (К_А, К_В) получателем В на основе начального условия должно быть простым.

— Отправитель А, зная открытый ключ К_А и сообщение М, может легко зашифровать М:

3. Получатель В, используя секретный ключ К_В и шифрограмму С, может легко восстановить М:

4. Противник, зная открытый ключ К_А, при попытке вычислить секретный ключ К_В наталкивается на непреодолимую вычислительную проблему.

5. Противник, зная пару (К_А, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему.

Криптосистема RSA

Алгоритм RSA предложен в 1978 г. тремя авторами: Райвестом (Rivest), Шамиром (Shamir) и Адлеманом (Adleman). Это первый полноценный алгоритм с открытым ключом, который может работать в режиме шифрования и ЭЦП. Алгоритм использует две однонаправленные функции: произведение больших простых чисел и модульную экспоненту.

Безопасность RSA базируется на трудности разложения большого числа на произведение двух простых чисел (факторизация).

Задача факторизации является трудно разрешимой задачей для больших значений модуля N.

Сначала авторы алгоритма RSA предлагали для вычисления модуля N выбирать простые числа Р и Q случайным образом, по 50 десятичных разрядов каждое. Считалось, что такие большие числа N очень трудно разложить на простые множители. Один из авторов алгоритма RSA, Р. Райвест, полагал, что разложение на простые множители числа из почти 130 десятичных цифр, приведенного в их публикации, потребует более 40 квадриллионов лет машинного времени. Однако этот прогноз не оправдался из-за сравнительно быстрого прогресса компьютеров и их вычислительной мощности, а также улучшения алгоритмов факторизации.

Криптосистемы RSA реализуются как аппаратным, так и программным путем.

Для аппаратной реализации операций шифрования и расшифрования RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах, позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время. И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.

Программная реализация RSA примерно в 100 раз медленнее программной реализации DES. С развитием технологии эти оценки могут несколько изменяться, но асимметричная криптосистема RSA никогда не достигнет быстродействия симметричных криптосистем.

Следует отметить, что малое быстродействие криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.