А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 5 страница
Перелом характеристики (в точке 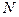 ) имеет место при внешней реактивности цепи к.з., равной
) имеет место при внешней реактивности цепи к.з., равной 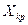 .
.
Продолжение прямых 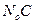 и
и 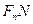 отсекает на оси напряжений отрезки пропорциональные соответственно
отсекает на оси напряжений отрезки пропорциональные соответственно 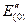
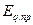 , а на оси токов – отрезки, пропорциональные токам
, а на оси токов – отрезки, пропорциональные токам 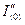 и
и 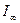 при к.з. на выводах генератора.
при к.з. на выводах генератора.
При одинаковых масштабах 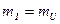
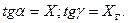
При 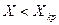 значения токов
значения токов 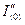 и
и 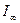 определяются соответственно абсциссами точек
определяются соответственно абсциссами точек 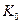 и
и 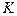 . При
. При 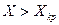 значения этих токов определяются абсциссами точек пересечения луча, проведенного из начала координат под углом
значения этих токов определяются абсциссами точек пересечения луча, проведенного из начала координат под углом 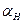 с прямыми
с прямыми 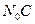 и
и 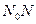 .
.
При отсутствии к.з. наклон луча 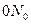 имеет наибольший угол (
имеет наибольший угол ( 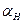 ), который пропорционален практически принимамой для нагрузки реактивности
), который пропорционален практически принимамой для нагрузки реактивности 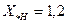 .
.

Рис.3.45.
Допустим, что в схеме участвует один генератор. Тогда несложно построить его внешнюю характеристику для момента времени 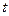 к.з. Для этого, задаваясь различными значениями внешней реактивности
к.з. Для этого, задаваясь различными значениями внешней реактивности 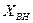 , подсчитаем ток к.з. в рассматриваемый момент времени к.з. согласно выражения (3.126), а по нему величину остаточного напряжения на шинах генератора. По полученным результатам можно построить для рассматриваемого момента времени внешнюю характеристику генератора
, подсчитаем ток к.з. в рассматриваемый момент времени к.з. согласно выражения (3.126), а по нему величину остаточного напряжения на шинах генератора. По полученным результатам можно построить для рассматриваемого момента времени внешнюю характеристику генератора 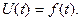
Пусть кривая 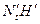 на рис. 3.45 представляет ту часть внешней характеристики генератора
на рис. 3.45 представляет ту часть внешней характеристики генератора 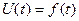 , которая соответствует работе генератора при подъеме его возбуждения от действия
, которая соответствует работе генератора при подъеме его возбуждения от действия  . Ее другая часть, соответствующая работе генератора при номинальном напряжении, представляется прямой
. Ее другая часть, соответствующая работе генератора при номинальном напряжении, представляется прямой 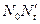 .
.
Наклон луча 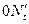 пропорционален внешней реактивности
пропорционален внешней реактивности 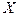 , при которой в рассматриваемый момент времени
, при которой в рассматриваемый момент времени 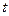 одновременно соблюдаются условия обоих режимов генератора. По аналогии с ранее установленным определением эта реактивность может быть названа критической реактивностью (
одновременно соблюдаются условия обоих режимов генератора. По аналогии с ранее установленным определением эта реактивность может быть названа критической реактивностью ( 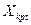 ) для данного момента времени
) для данного момента времени 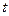 .
.
Гиперболическая зависимость между 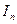 и
и 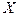 , устанавливаемая выражением (3.150), имеет место лишь при прямолинейной внешней характеристике генератора.
, устанавливаемая выражением (3.150), имеет место лишь при прямолинейной внешней характеристике генератора.
Чтобы определить искомые приближенные значения расчетной э.д.с. 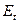 и расчетной реактивности
и расчетной реактивности 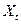 генератора для момента времени
генератора для момента времени 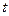 нужно соответствующую этому моменту времени внешнюю характеристику генератора (
нужно соответствующую этому моменту времени внешнюю характеристику генератора ( 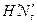 ) заменить подходящей прямой (
) заменить подходящей прямой ( 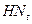 ), продолжение которой до пересечения с осью напряжений даст значение
), продолжение которой до пересечения с осью напряжений даст значение 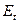 , а ее наклон к оси токов, то есть
, а ее наклон к оси токов, то есть 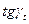 - значение
- значение 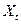 .
.
Таким путем можно определить расчетные 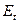 и
и 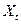 , а также
, а также 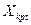 для различных моментов времени. Из сказанного понятно происхождение названия рассматриваемого метода.
для различных моментов времени. Из сказанного понятно происхождение названия рассматриваемого метода.
Если для генератора с 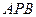 найдены его расчетные
найдены его расчетные 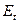 и
и 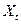 , периодическую слагающую тока трехфазного к.з. в соответствующий момент времени определяют аналогично тому, как это делалось для расчета установившегося режима к.з.
, периодическую слагающую тока трехфазного к.з. в соответствующий момент времени определяют аналогично тому, как это делалось для расчета установившегося режима к.з.
По аналогии с (3.40) для произвольного момента времени можно написать:
критическая реактивность 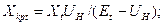 (3.151)
(3.151)
и критический ток 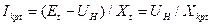 . (3.152)
. (3.152)
Таким образом, если внешняя реактивность 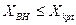 , то генератор работает в режиме подъема возбуждения и должен быть введен в схему замещения своими
, то генератор работает в режиме подъема возбуждения и должен быть введен в схему замещения своими 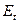 и
и 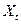 ; если
; если 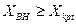 , то генератор должен быть введен в схему своими
, то генератор должен быть введен в схему своими 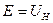 и
и 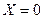 , что соотвествует его работе в режиме номинального напряжения.
, что соотвествует его работе в режиме номинального напряжения.
Изложенный путь нахождения 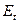 и
и 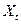 можно использовать для каждого генератора.
можно использовать для каждого генератора.
Однако в большинстве случаев достаточно ограничиться применением расчетных 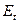 и
и 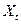 , найденных для типовых машин.
, найденных для типовых машин.
Для отечественных генераторов средней мощности в справочниках приводятся семейства кривых 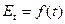 и
и 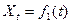 , выраженные в относительных единицах при номинальных условиях работы генератора, при разных значениях предшествующего тока возбуждения
, выраженные в относительных единицах при номинальных условиях работы генератора, при разных значениях предшествующего тока возбуждения 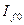 .
.
Пример таких кривых приведен на рис.3.46.
Если действительные параметры генератора существенно отличаются от типовых, при которых пострены данные кривые, то значения 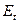 и
и 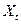 такого генератора приближенно могут быть найдены из выражений:
такого генератора приближенно могут быть найдены из выражений:
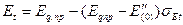 (3.153)
(3.153)
и 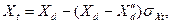 (3.154)
(3.154)
 |
где
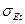 и
и 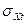 - коэффициенты,значения которых определяются по кривым рис.3.46.
- коэффициенты,значения которых определяются по кривым рис.3.46.
Рис.3.46.
Принципиальным и главным допущением рассматриваемого метода в его применении к сложным схемам является использование расчетных 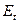 и
и 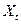 , которые справедливы лишь для элементарной схемы (то есть схемы с одним генератором).
, которые справедливы лишь для элементарной схемы (то есть схемы с одним генератором).
Тем не менее, этот метод часто позволяет с достаточной для практики точностью определять для промежуточных моментов времени процесса к.з. ток не только в месте к.з., но также (что особенно важно) в других ветвях схемы.
Общий порядок выполнения расчета по методу спрямленных характеристик полностью идентичен порядку расчета установившегося режима к.з.
При этом для рассматриваемого момента времени 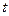 все генераторы с
все генераторы с 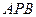 в зависимости от ожидаемого для них режима должны быть введены в схему замещеия своими
в зависимости от ожидаемого для них режима должны быть введены в схему замещеия своими 
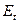 и
и 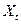 либо
либо 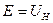 и
и 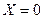 , генераторы без
, генераторы без  -
-
своими 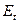 и
и 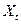 .
.
Для предварительного выбора возможного режима генератора с 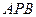 следует сопоставить величину его
следует сопоставить величину его 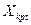 с внешней реактивностью схемы по отношению к данному генератору, оценка которой в общем случае может быть сделана лишь в первом приближении.
с внешней реактивностью схемы по отношению к данному генератору, оценка которой в общем случае может быть сделана лишь в первом приближении.
Для 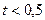 с, имея ввиду еще малое влияние
с, имея ввиду еще малое влияние 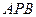 , все генераторы с
, все генераторы с 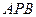 можно вводить своими
можно вводить своими 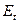 и
и 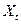 , то есть считать, что они работают в режиме подъема возбуждения. Нагрузки должны быть введены в схему замещения в точках их действительного присоединения, принимая их реактивность
, то есть считать, что они работают в режиме подъема возбуждения. Нагрузки должны быть введены в схему замещения в точках их действительного присоединения, принимая их реактивность 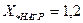 и э.д.с.
и э.д.с. 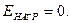
После того, как для заданной схемы замещения будут найдены ее 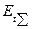 и
и 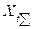 относительно точки к.з., значение периодической слагающей тока в месте к.з. определяют как
относительно точки к.з., значение периодической слагающей тока в месте к.з. определяют как 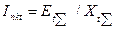 .
.
Далее следует проверить правильность выбранных режимов генеторов с 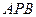 .
.
Для этого необходимо, развертывая схему замещения, найти токи генераторов или напряжения на их выводах. При этом, для режима номинального напряжения должно быть 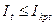 , а при режиме подъема возбуждения
, а при режиме подъема возбуждения 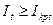 или, иначе
или, иначе 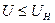 .
.
Если окажется, что у некоторых генераторов режимы выбраны неверно, то их следует соответственно изменить и затем повторить аналогичный расчет с последующей проверкой.
3.6.6.Метод типовых кривых
Методы расчетных кривых и спрямленных характеристик основаны на использовании данных синхронных машин мощностью до 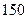 МВт. Эти методы не позволяют с приемлемой точностью определять токи, необходимые для выбора высоковольтных выключателей, особеннно при современных крупных генераторах.
МВт. Эти методы не позволяют с приемлемой точностью определять токи, необходимые для выбора высоковольтных выключателей, особеннно при современных крупных генераторах.
Поэтому в последнем случае рекомендуется к применению практический метод расчета - метод типовых кривых (см. рис.3.47)
По найденному начальному току к.з. 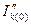 этим методом можно определить периодическую и апериодическую составляющие тока к.з. в момент расхождения контактов выключателя, необходимые для выбора последнего.
этим методом можно определить периодическую и апериодическую составляющие тока к.з. в момент расхождения контактов выключателя, необходимые для выбора последнего.
Заметим, что параметры турбо- и гидрогенераторов одной и той же мощности различны. Кроме того, однотипные генераторы, как правило, также имеют различные параметры ( 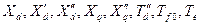 и т.д.). Поэтому характер изменения тока во времени будет различен даже при одинаковой удаленности к.з.
и т.д.). Поэтому характер изменения тока во времени будет различен даже при одинаковой удаленности к.з.

Рис.3.47.
Авторам метода типовых кривых[3] по уравнениям Парка-Горева удалось получить средние кривые изменения тока во времени (в относительных единицах) между кривыми турбо – и гидрогенераторов, максимальная погрешность усреднения которых не превышает 10%.
При построении типовых кривых значения вычисленных токов к.з. генераторов 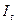 для различных моментов времени были отнесены к начальным свехпереходным токам генераторов
для различных моментов времени были отнесены к начальным свехпереходным токам генераторов 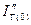 .
.
Для учета удаленности к.з. было введено отношение 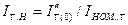 - характеризующее кратность начального тока к.з. к номинальному току генератора.
- характеризующее кратность начального тока к.з. к номинальному току генератора.
Очевидно, что, чем ближе к.з. к генератору, тем больше это отношение.
Таким образом, типовые кривые представляют собой семейство кривых 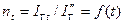 при
при 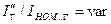 , которые характеризуют изменения тока без определения его величины (то есть в относительных единицах). Для учета влияния на ток к.з. источника неограниченной мощности введены семейства дополнительных зависимостей
, которые характеризуют изменения тока без определения его величины (то есть в относительных единицах). Для учета влияния на ток к.з. источника неограниченной мощности введены семейства дополнительных зависимостей 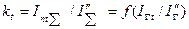 при
при 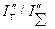 =
= 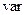 .
.
Кривые унифицированы: для турбогенераторов от 12 до 800 МВт; для гидрогенераторов до 500 МВт; для синхронных компенсаторов от 37, 5 до 100 Мвар, имеющих вентильную систему возбуждения ( рабочая) и машинную систему возбуждения ( резервная).
Типовые кривые построены для определения периодической слагающей тока к.з. в генераторе на двух временных интервалах: от 0 до 0,5 с и от 0,5 до 3 с., а также с учетом влияния энергосистемы на двух временных интервалах: от 0 до 0, 5 с и от 0,5 с до 3 с.
 |
Из графика типовых кривых следует, что для нахождения абсолютных значений токов в любой момент времени прежде всего нужно определить начальный сверхпереходный ток генератора
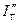 , который рассчитывается обычным способом после преобразования исходной схемы к виду рис.3.48,
, который рассчитывается обычным способом после преобразования исходной схемы к виду рис.3.48, 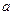 .
.
Рис.3.48.
Во многих случаях не удается всю электрическую систему представить одним эквивалентным генератором, так как многие генераторные станции
бывает значительно удалены от места к.з. и ток к.з., посылаемый от них в место к.з., изменяется во времени незначительно. Поэтому такие генераторные станции объединяются во второй источник – систему неограниченной мощности. Схема замещения при этом приводится к виду рис.3.48, 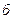 .
.
Для учета влияния системы на общий ток к.з. С.А.Ульяновым была предложена еще одна зависимость (см. рис.4.47, 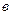 ), удобная для непосредственного определения тока в месте к.з.
), удобная для непосредственного определения тока в месте к.з.
Приведем порядок действий при расчете тока к.з. по методу типовых кривых, соответственно, для результирующих схем замещения рис.3.48,а и 3.48,б.
Для результирующей схемы замещения рис.3.48, а:
1.Система представляется одним или несколькими обобщенными генераторами, радиально связанными с местом к.з. (объединяемые генераторы находятся примерно в одинаковых условиях).
2.Составляется схема замещения для расчета начального тока к.з., которая преобразовывается к виду рис.3.48, 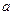 , для каждой выделенной радиальной генерирующей ветви.
, для каждой выделенной радиальной генерирующей ветви.
3. Определяются номинальный 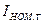 и начальный ток к.з. генератора
и начальный ток к.з. генератора 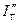 , для каждой выделенной радиальной генерирующей ветви.
, для каждой выделенной радиальной генерирующей ветви.
4.Определяется кратность начального тока к.з. генератора выделенной радиальной генерирующей ветви 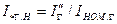 .
.
5. По типовым кривым и величине 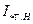 определяется значение
определяется значение 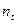 для заданного момента времени к.з.(рис.3.47, а, б)
для заданного момента времени к.з.(рис.3.47, а, б)
6.Определяется посылаемый ток к.з. выделенной радиальной генерирующей ветви 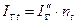 в именованных единицах.
в именованных единицах.
Для результирующей схемы замещения рис.3.48, б:
1.Система представляется генератором и шинами неизменного напряжения (генераторы находятся в резко отличных условиях и связаны с местом к.з. через общие сопротивления).
2. Составляется схема замещения для расчета начального тока к.з., которая преобразовывается к виду рис.3.48, б.
3. Определяются номинальный 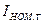 и начальный ток к.з. генератора
и начальный ток к.з. генератора 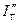 , а также начальный ток
, а также начальный ток 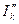 .
.
4.Определяются кратность начального тока к.з. генератора 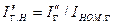
и доля тока к.з.генератора в общем токе к.з. для начального момента времени 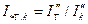 .
.
5. По типовым кривым, величинам 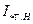 и
и 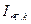 определяются значение
определяются значение 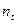 и
и 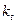 для заданного момента времени к.з.(рис.3.47, а, б, в).
для заданного момента времени к.з.(рис.3.47, а, б, в).
6. Определяется ток генератора 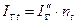 и ток к.з.
и ток к.з. 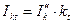 в именованных единицах.
в именованных единицах.
4. ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ
НАРУШЕНИИ СИММЕТРИИ ТРЕХФАЗНОЙ ЦЕПИ
4.1. Общие замечания
Рассматриваемые ниже несимметричные переходные процессы ограничены условием, что несимметрия возникает в одном каком-либо месте системы, в то время как вся остальная часть последней остается строго симметричной.
Такая однократная несимметрия может быть поперечной – любой вид несимметричного к.з. или продольной – обрыв одной или двух фаз.
Строгий математический анализ несимметричных переходных процессов затруднен тем, что при таких процессах образуется пульсирующее магнитное поле ротора, которое образует полный спектр высших гармоник. При этом переход от фазных переменных (А, В, С) к переменным в координатах d,q,0 не освобождает дифференциальные уравнения от периодических коэффициентов.
Для стационарных условий обычно определяют лишь основные гармоники искомых величин, что позволяет применить для анализа метод симметричных составляющих.
Именно при таком ограничении, данный метод используется также в условиях несимметричных переходных процессов.
4.2. Метод симметричных составляющих
В соответствии с этим методом любую систему трех несимметричных векторов можно разложить на три системы векторов:
симметричную систему трех векторов прямой последовательности, симметричную систему трех векторов обратной последовательности и симметричную систему векторов нулевой последовательности.
Графически это можно представить так, как показано на рис.4.1.
Аналитически это можно записать в следующем виде:
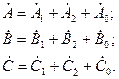 (4.1)
(4.1)
Из приведенной системы (4.1) видно, что она содержит 9 неизвестных векторов (составляющих исходной трехфазной несиметричной системы векторов), которые связаны между собой тремя уравнениями. Решение системы уравнений (4.1) в представленном виде невозможно.
Для ее решения следует воспользоваться свойсвами систем симметрич-
ных составляющих: в каждой трехфазной системе симметричных составля-
ющих векторы фаз А, В, и С одинаковы по модулю; векторы фаз систем симметричных составляющих прямой и обратной последовательностей сдвинуты относительно друг друга на 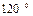 , а
, а
 |
векторы фаз нулевых составляющих одинаково направлены.
Рис.4.1.
а- трехфазные системы векторов прямой, обратной и нулевой последовательностей;
б – порядок получения исходных фазных векторов и исходной несимметричной
трехфазной системы векторов
Для решения системы (4.1.) нужно ввести единичный вектор 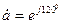 , позволяющий свести систему (4.1) к системе трех уравнений с тремя неизвестными
, позволяющий свести систему (4.1) к системе трех уравнений с тремя неизвестными 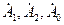 .
.
Дело в том, что если любой вектор умножить на 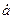 , то модуль вектора не изменится, а лишь произойдет его поворот на угол
, то модуль вектора не изменится, а лишь произойдет его поворот на угол 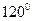 против направления движения стрелки часов.
против направления движения стрелки часов.
Таким образом систему (4.1) можно переписать в следующем виде:
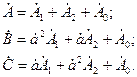 (4.2)
(4.2)
Учитывая что 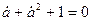 , получим при решении (4.2) следующие соотношения:
, получим при решении (4.2) следующие соотношения:
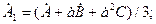 (4.3)
(4.3)
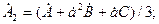 (4.4)
(4.4)
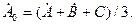 (4.5)
(4.5)
Таким образом, было показано, что, если система (4.1) позволяет по известным симметричным составляющим фазных величин определить несимметричные векторы исходной трехфазной системы, то соотношения (4.3)-(4.5) позволяют решить обратную задачу – определить по известным несимметричным векторам трехфазной системы их симметричные состав-
ющие.
Согласно ГОСТ абсолютную величину отношения составляющей обратной последовательности к составляющей прямой последовательности называют коэффициентом несимметрии исходной системы, то есть

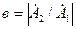 , (4.6)
, (4.6)
а абсолютную величину отношения составляющей нулевой последователь-
носим к составляющей прямой последовательности называют коэффициен-
том неуравновешенности системы
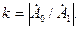 . (4.7)
. (4.7)
Как следует из рис.4.1, системы вектров прямой и обратной последовате-
льностей являются симметричными и уравновешенными. Система векторов нулевой последовательности является симметричной,но неуравновешенной.
Понятию систем векторов – токов прямой, обратной и нулевой последо-
вательностей соответствует понятие сопротивлений прямой последователь-
ности 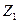 , обратной последовательности
, обратной последовательности 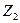 и нулевой последовательности
и нулевой последовательности 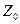 .
.
Условились считать, что генератор создает только э.д.с. прямой последо-
вательности, а э.д.с. обратной и нулевой последовательностей следует учи-
тывать в виде падений напряжения с обратным знаком, которые приложены к точке к.з.
Поэтому для точки к.з. связь между симметричными составляющими напряжения и падениями напряжений для различных последовательностей будет (например, для фазы  , принимая, что
, принимая, что 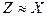 ):
):
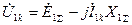 ; (4.8)
; (4.8)
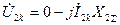 ; (4.9)
; (4.9)
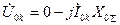 . (4.10)
. (4.10)
Как следует из (4.8)-(4.10) каждое соотношение связывает два неизвест-
ных: 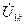 и
и 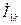 ,
, 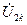 и
и 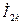 ,
, 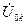 и
и 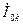 и в таком виде эти соотношения не могут быть решены.
и в таком виде эти соотношения не могут быть решены.
Для решения соотношений (4.8)-(4.10) необходимы еще три уравнения, кеоторые определяют из начальных условий для конкретных случаев несимметрии.
Дата добавления: 2016-04-14; просмотров: 1242;
