А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 2 страница
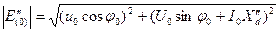 , (3.63)
, (3.63)
или приближенно
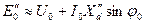 . (3.63, а)
. (3.63, а)
Такие допущения при определении токов в цепи статора синхронной машины вносят погрешность не более 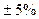 . Они, конечно, непригодны, если требуется определить токи в цепях ротора.
. Они, конечно, непригодны, если требуется определить токи в цепях ротора.
Таким образом, для расчета 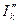 , возникающего при внезапном нарушении режима, следует составить схему замещения, вводя в нее все генераторы, крупные синхронные и асинхронные двигатели, компенсаторы, а также обобщенные нагрузки отдельных мощных узлов энергосистемы своими приведенными к основной ступени напряжения значениями
, возникающего при внезапном нарушении режима, следует составить схему замещения, вводя в нее все генераторы, крупные синхронные и асинхронные двигатели, компенсаторы, а также обобщенные нагрузки отдельных мощных узлов энергосистемы своими приведенными к основной ступени напряжения значениями 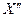 и
и 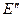 .
.
Дальнейшее преобразование схемы замещения производится согласно указаниям раздела 2.
В частности, абсолютная величина начального сверхпереходного тока в месте трехфазного к.з. также может быть определена как
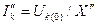 S, (3.64)
S, (3.64)
где 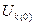 - предшествующее напряжение в месте к.з.;
- предшествующее напряжение в месте к.з.; 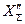 - результирующая реактивноcть схемы замещения отноcительно точки к.з.
- результирующая реактивноcть схемы замещения отноcительно точки к.з.
Пуск двигателя по существу можно рассматривать как возникновение к.з. за реактивностью 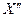 данного двигателя, то есть
данного двигателя, то есть 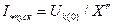 .
.
На практике при выполнении расчетов начального сверхпереходного тока в месте к.з. обычно учитывают только те обобщенные нагрузки и отдельные
двигатели, которые непосредственно связаны с точкой к.з. или находятся в зоне малой электрической удаленности от нее.
При определении ударного тока обычно учитывают затухание аперидиче-
ской слагающей тока к.з., считая, что амплитуда сверхпереходного тока за полпериода сохраняет свое начальное значение. При этом ударный ток, определяемый для наиболее тяжелых условий, будет
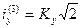
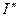 . О (( (3.65)
. О (( (3.65)
Как известно, ударный коэффициент 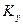 ззавсит от значения постоянной времени цепи к.з.
ззавсит от значения постоянной времени цепи к.з. 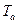 или от отношения ХS/rS. Эта зависимость показана на рис. 3.29.
или от отношения ХS/rS. Эта зависимость показана на рис. 3.29.
С целью упрощения расчетов для разветвленной схемы определяют значение эквивалентной постоянной времени
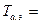 ХS/(rSw),
ХS/(rSw),
где ХS - суммарное индуктивное сопротивление схемы замещения, рассчитанное при отсутствии в схеме всех активных сопротивлений;
rS - суммарное активное сопротивление схемы, найденное при отсутствии в ней всех индуктивных сопротивле- ний.

При отдельном учете влияния асинхронных двигателей ударный ток в месте к.з. определяют как 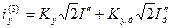 , (3.66)
, (3.66)
где 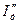 и
и 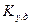 -начальный сверхпере-
-начальный сверхпере-
………………Рис.3.29 ходный ток и ударный коэффициент асинхронных двигателей.
 На рис.3.30. представлена зависимость
На рис.3.30. представлена зависимость 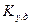 от номинальной мощности двигателей, где заштрихованная зона указывает диапазон отклонения этого коэффициента от среднего значения (средняя кривая). Для мелких двигателей (
от номинальной мощности двигателей, где заштрихованная зона указывает диапазон отклонения этого коэффициента от среднего значения (средняя кривая). Для мелких двигателей ( 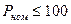 кВт), а также для обобщенной нагрузки практически
кВт), а также для обобщенной нагрузки практически 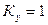 .
.
У синхронных двигателей величина ударного коэффициента примерно та же, что и у синхронных генераторов равновеликой мощности.
При отсутствии необходимых данных для оценки величины отношения 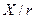 у отдельных элементов можно ориенти-
у отдельных элементов можно ориенти-
роваться на указанные в таблице Рис.3.30. пределы этого отношения.
Таблица
Значения 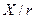 для элементов электрической системы
для элементов электрической системы
| Наименование элемента | Отношение 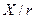
|
| Турбогенераторы мощностью до 100 МВт | 15-85 |
| То мощностью 100-500 МВт | 100-1400 |
| Гидрогенераторы с демпферными обмотками | 40-60 |
| То же без демпферных обмоток | 60-90 |
| Трансформаторы мощностью 5-30 МВА | 7-17 |
| То же мощностью 60-500 МВА | 20-50 |
| Реакторы 6-10 кВ до 1000А | 15-70 |
| То же 1500 А и выше | 40-80 |
| Воздушные линии | 2-8 |
Кабели 6-10 кВ с медными и алюминиевыми жилами сечением 3х95-3х185 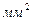
| 0,2-0,8 |
| Обобщенная нагрузка | 2,5 |
В заключение данного параграфа остановимся еще на вопросе несинхрон-
ного включения генератора.
Пусть система, к которой подключается генератор, характеризуется напряжением 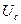 и реактивностью
и реактивностью 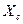 .
.
Определим, при каких условиях начальное значение сверхпереходного тока при несинхронном включении не превзойдет начального значения сверхпереходного тока генератора при трехфазном к.з. на его выводах. Для этого, очевидно, должно выполняться следующее неравенство:
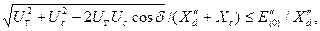
где 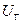 и
и 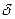 - напряжение на шинах генератора и угол сдвига вектора этого напряжения относительно вектора напряжения системы;
- напряжение на шинах генератора и угол сдвига вектора этого напряжения относительно вектора напряжения системы; 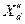 и
и 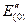 -сверхпереходные реактивность и э.д.с. генератора.
-сверхпереходные реактивность и э.д.с. генератора.
При равенстве модулей 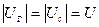 поставленное условие будет выполнено, если
поставленное условие будет выполнено, если 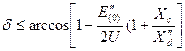 .
.
 |
Эта зависимость при
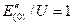 представлена на рисунке.
представлена на рисунке.
3.4. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПЕРЕХОДНОГО ПРОЦЕССА СИНХРОННОЙ МАШИНЫ
3.4.1. Общие замечания и допущения
Аналитическое исследование электромагнитного переходного процесса синхронной машины с учетом всех влияющих на него факторов представля-
ет весьма сложную задачу.
Поэтому для упрощения ее решения вводят ряд допущений:
1. Магнитная система синхронной машины ненасыщенна (индуктивности машины не зависят от величин токов).
2. Распределение кривых н.с. и индукции в воздушном зазоре принимают синусоидальным, соответственно, наведенные в статоре э.д.с. выражаются синусоидами основной частоты.
3. Наличие полной симметрии фазных обмоток статора; ротор симметричен относительно своих осей 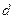 и
и 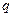 .
.
4. Предполагается, что все демпферные обмотки на роторе по продольной
оси заменены одной эквивалентной продольной демпферной обмоткой; аналогично, предполагается, что в поперечной оси ротора также имеется только одна эквивалентная поперечная демпферная обмотка.
5.Частота вращения ротора машины в течение всего рассматриваемого переходного процесса постоянна и равна синхронной.
6. В магнитной системе отсутствуют потери.
3.4.2. Исходные уравнения
 |
Принципиальная схема синхронной машины, ротор которой имеет явно выраженные полюсы, представлена на рис.3.31.
Рис.3.31.
На рис.3.31 стрелками указаны принятые положительные направления токов и напряжений в обмотках статора и ротора, а также положительны направления магнитных осей фазных обмоток статора ( 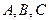 ) и магнитных осей ротора (
) и магнитных осей ротора ( 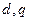 ).
).
Дифференциальные уравнения равновесия э.д.с. и падений напряжения в каждой из обмоток имеют вид:
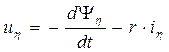 ;
;
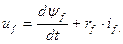 (3.67)
(3.67)
где 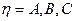 - индекс фазы для обмотки статора;
- индекс фазы для обмотки статора;
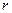 и
и 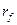 - активные сопротивления, соответственно, контуров каждой фазы статора и цепи возбуждения;
- активные сопротивления, соответственно, контуров каждой фазы статора и цепи возбуждения;
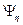 и
и 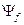 - результирующие потокосцепления соответствующих обмоток, включая их потокосцепления рассеяния.
- результирующие потокосцепления соответствующих обмоток, включая их потокосцепления рассеяния.
Раскроем выражения для потокосцеплений учитывая, что при принятых допущениях они представляют собой линейные зависимости от тока соответствующего контура и токов магнитосвязанных с ним других контуров.
Коэффициентами пропорциональности при этом будут индуктивность 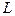 рассматриваемого контура и его взаимоиндуктивности
рассматриваемого контура и его взаимоиндуктивности 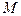 с другими контурами.
с другими контурами.
Введя у 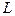 и
и 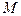 индексы соответствующих обмоток, можно записать:
индексы соответствующих обмоток, можно записать:
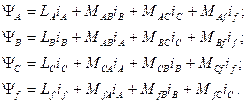 (3.68)
(3.68)
Если бы все 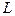 и
и 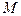 оставались неизменными при вращении ротора, то система (3.67) состояла бы из линейных дифференциальных уравнений с постоянными коэффициентами. Однако, во вращающейся машине это не имеет место. Кроме индуктивности обмотки возбуждения
оставались неизменными при вращении ротора, то система (3.67) состояла бы из линейных дифференциальных уравнений с постоянными коэффициентами. Однако, во вращающейся машине это не имеет место. Кроме индуктивности обмотки возбуждения 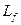 все остальные индуктивности и коэффициенты взаимоиндукции зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.
все остальные индуктивности и коэффициенты взаимоиндукции зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.
В этой связи, систему (3.67) непосредственно решить невозможно, что обусловливает необходимость искать другие (нестандартные) пути решения задачи.
Рассмотрим закономерности изменения индуктивностей обмоток синхронной машины при вращении ротора.
3.4.3. Индуктивности обмоток синхронной машины
Пусть углом 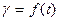 мы будем фиксировать положение ротора: между продольной осью
мы будем фиксировать положение ротора: между продольной осью 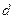 и магнитной осью фазы
и магнитной осью фазы 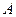 (рис.3.32).
(рис.3.32).
Синусоидальность наводимых в статоре э.д.с. холостого хода указывает на закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора.
 Очевидно, он выражается синусои-
Очевидно, он выражается синусои-
дальной функцией с периодом 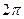 (для двухполюсной машины это соответст-
(для двухполюсной машины это соответст-
вует одному обороту ротора),максимум которой ( 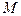 )наступает при совпа-
)наступает при совпа-
дении магнитных осей этих обмоток.
Так, например, для фазы 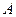 получим
получим
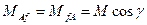 . (3.69)
. (3.69)
Изменение индуктивностей фазных обмоток и взаимных индуктивностей между этими обмотками обусловлено
………………Рис.3.32. вращением явнополюсного ротора, при вращении которого непрерывно меняется сопротивление магнитным потокам, определяющие данные индуктивности.
Изменение магнитных потоков происходит гармонически с периодом 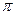 , то есть в два раза меньшим, чем в случае изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора (при повороте ротора на угол
, то есть в два раза меньшим, чем в случае изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора (при повороте ротора на угол 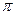 повторяется предыдущий цикл изменения магнитного сопротивления).
повторяется предыдущий цикл изменения магнитного сопротивления).
В практических расчетах ограничиваются приближенными выражениями для этих индуктивностей (при разложении функции в ряд Фурье, изменяющейся по закону косинуса, пренебрегают всеми четными высшими гармониками).
Так индуктивности фаз рассчитывают следующим образом[2]:
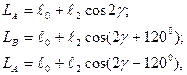 (3.70)
(3.70)
а взаимные индуктивности между обмотками:
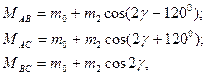 (3.71)
(3.71)
где 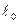 и
и 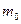 - постоянные составляющие соответствующих индуктивностей;
- постоянные составляющие соответствующих индуктивностей;
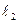 и
и 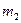 - амплитуды вторых гармоник тех же индуктивностей.
- амплитуды вторых гармоник тех же индуктивностей.
В свою очередь, коэффициенты 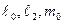 и
и 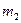 выражаются через постоянные индуктивности, которыми характеризуется синхронная машина:
выражаются через постоянные индуктивности, которыми характеризуется синхронная машина:
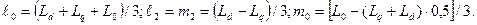 (3.72)
(3.72)
3.4.4. Обобщенный вектор трехфазной системы
 |
Вместо представления величин трехфазной системы звездой векторов,проекции которых на ось времени
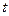 дают мгновенные значения этих величин в фазах, можно получить те же мгновенные значения, проектируя единый вектор на три оси времени, каждая из которых сопадает с магнитной осью соответствующей фазы (рис.3.33).
дают мгновенные значения этих величин в фазах, можно получить те же мгновенные значения, проектируя единый вектор на три оси времени, каждая из которых сопадает с магнитной осью соответствующей фазы (рис.3.33).
Рис.3.33.
Такой вектор называют обобщенным вектором трехфазной системы. При его вращении в ту же сторону, что и системы трех векторов, чередование осей времени фаз следует изменить на противоположное.
При симметричном установившемся режиме конец обобщенного вектора описывает с постоянной скоростью окружность, а его величина будет равна амплитуде рассматриваемой величины.
Обобщенным вектором можно характеризовать любые фазные переменные 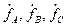 , изменяющиеся по произвольному закону при соблюдении единственного условия
, изменяющиеся по произвольному закону при соблюдении единственного условия 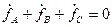 . (3.73)
. (3.73)
 Модуль искомого обобщенного вектора
Модуль искомого обобщенного вектора 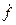 может определен из очевидных равенств (рис.3.34)
может определен из очевидных равенств (рис.3.34) 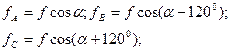 (3.74)
(3.74)
для чего достаточно их возвести в квадрат и просуммировать:
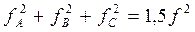 ,
,
откуда 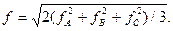 (3.75)
(3.75)
Рис.3.34.
Возможность представления трехфазной системы векторов одним обобщенным вектором упрощает выражения связей между статором и ротором, что позволяет в дифференциальных уравнениях переходного процесса синхронной машины освободиться от переменных коэффициентов.
3.4.5. Замена переменных
На рис. 3.34 обобщенный вектор 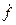 определен в трехосной системе координат ( в фазных осях времени). Тот же вектор можно выразить иначе, например, в двухосной системе координат. Для решения нашей задачи удобно в качестве двухосной системы координат выбрать декартовы ортогональные координаты, жестко связанные с ротором машины. При этом, чтобы ротор был расположен симметрично относительно осей координат, их совмещают соответственно с продольной
определен в трехосной системе координат ( в фазных осях времени). Тот же вектор можно выразить иначе, например, в двухосной системе координат. Для решения нашей задачи удобно в качестве двухосной системы координат выбрать декартовы ортогональные координаты, жестко связанные с ротором машины. При этом, чтобы ротор был расположен симметрично относительно осей координат, их совмещают соответственно с продольной 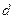 и поперечной
и поперечной 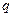 осями ротора.
осями ротора.
Эту систему координат сокращенно называют и обозначают 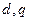 (рис.3.35).
(рис.3.35).
 Здесь угол
Здесь угол 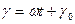 является функцией времени и отражает вращение ротора с угловой частотой
является функцией времени и отражает вращение ротора с угловой частотой 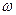 , которая в общем случае может быть переменной.
, которая в общем случае может быть переменной.
Проектируя вектор 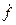 на оси
на оси 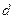 и
и 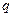 получим его проекции,
получим его проекции, 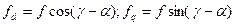 (3.76)
(3.76)
связь которых c фазными переменными определяется равенствами: 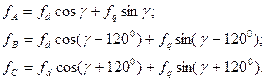 (3.77) - Рис.3.35.
(3.77) - Рис.3.35.
Решив (3.77) относительно новых переменных, найдем
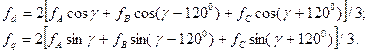 (3.78)
(3.78)
До сих пор нами предполагалось, что трехфазная система векторов удовлетворяет условию (3.73). Однако, если сумма фазных переменных (проекции на ось времени 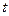 ) не равна нулю, то ее можно выразить через новую переменную
) не равна нулю, то ее можно выразить через новую переменную 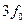 , то есть
, то есть
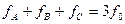 . (3.79)
. (3.79)
Поскольку составляющая 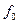 во всех фазах одинакова, то она не влияет на величину и положение в пространстве обобщенного вектора
во всех фазах одинакова, то она не влияет на величину и положение в пространстве обобщенного вектора 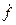 , ни на его составляющие
, ни на его составляющие 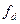 и
и 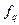 .
.
В этом можно убедиться, подставив в (3.78) вместо 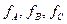 соответственно
соответственно 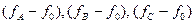 , которые удовлетворяют условию (3.73).
, которые удовлетворяют условию (3.73).
Таким образом, три переменные в координатах 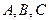 можно однозначно заменить другими тремя переменными в координатах
можно однозначно заменить другими тремя переменными в координатах 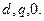 При этом в общем случае при переходе к фазным переменным необходимо в каждом из равенств (3.77) прибавить нулевую составляющую, то есть
При этом в общем случае при переходе к фазным переменным необходимо в каждом из равенств (3.77) прибавить нулевую составляющую, то есть
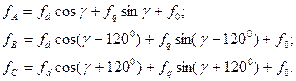 (3.80)
(3.80)
Переход от трехосной ( 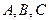 ) к двухосной системе координат (
) к двухосной системе координат ( 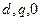 ) соответствует тому, что трехфазная машина по существу заменена эквивалентной двухфазной.
) соответствует тому, что трехфазная машина по существу заменена эквивалентной двухфазной.
Именно по этой причине целесообразно перейти от переменных в координатах 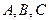 к переменным в координатах
к переменным в координатах 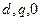 . Такой переход позвляет уравнения (3.67) преобразовать в дифференциальные уравнения с постоянными коэффициентами.
. Такой переход позвляет уравнения (3.67) преобразовать в дифференциальные уравнения с постоянными коэффициентами.
Рассмотренное выше преобразование впервые было предложено Блонделем для установившегося режима явнополюсной синхронной машины и впоследствии было развито Парком и Горевым для условий переходного процесса.
3.4.6. Преобразование уравнений
Применим полученные результаты для преобразования исходных дифференциальных уравнений (3.67). В соответствии с (3.80) выразим ток, напряжение и потокосцепление фазы 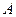 через новые переменные:
через новые переменные:
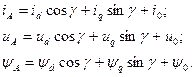 (3.81)
(3.81)
Подставим их в первое уравнение (3.67), имея в виду, что 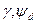 и
и 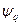 являются функциями времени
являются функциями времени 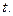 После подстановки получим:
После подстановки получим:

Сгруппируем слагаемые относительно 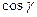 и
и 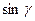 , получим
, получим
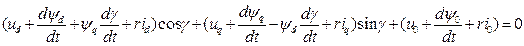 . (3.82)
. (3.82)
Уравнение (3.82) должно быть удовлетворено при любых значениях угла 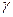 , что возможно только при условии, что каждое из выражений, заключенных в скобки, тождественно равно нулю.Таким образом, уравнение (3.82) (для фазы
, что возможно только при условии, что каждое из выражений, заключенных в скобки, тождественно равно нулю.Таким образом, уравнение (3.82) (для фазы 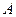 ) распадается на три уравнения
) распадается на три уравнения

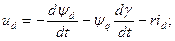 (3.83)
(3.83)
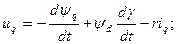 (3.84)
(3.84)

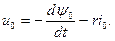 (3.85)
(3.85)
При записи (3.83)-(3.85) в относительных единицах потокосцепления можно представить в следующем виде
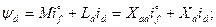 (3.86)
(3.86)
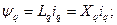 (3.87)
(3.87)
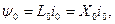 (3.88)
(3.88)
где 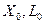 -реактивность и индуктивность нулевой последовательности машины.
-реактивность и индуктивность нулевой последовательности машины.
Отметим еще раз, что в (3.82)-(3.86) токи 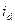 и
и 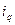 представляют собой проекции обобщенного вектора тока статора
представляют собой проекции обобщенного вектора тока статора 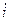 на оси
на оси 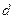 и
и 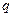 .
.
Таким образом, переход к новым переменным в координатах 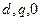 позволил преобразовать систему (3.67) в уравнения (3.82)-(3.86), где все коэффициенты постоянные величины.
позволил преобразовать систему (3.67) в уравнения (3.82)-(3.86), где все коэффициенты постоянные величины.
Уравнения (3.83)-(3.85) выражают основу теории двух реакции синхронной машины при электромагнитном переходном процессе. Эти уравнения называют уравнениями Парка-Горева.
Если изменения угла 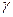 , характеризующие движение ротора, выразить соответствующим уравнением, то вместе с ранее составленными уравнениями для цепей ротора и статора получим систему уравнений, которая будет отражать одновременное протекание электромагнитного и электромеханического переходного процессов с учетом их взаимного влияния.
, характеризующие движение ротора, выразить соответствующим уравнением, то вместе с ранее составленными уравнениями для цепей ротора и статора получим систему уравнений, которая будет отражать одновременное протекание электромагнитного и электромеханического переходного процессов с учетом их взаимного влияния.
Для анализа только электромагнитного переходного процесса в соответствии с допущением 5 в дальнейшем будем считать
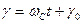 ,
,
где 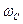 - синхронная угловая частота;
- синхронная угловая частота; 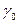 - начальный угол.
- начальный угол.
Следовательно, в этом случае 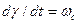 и в относительных единицах при
и в относительных единицах при 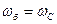 получим
получим 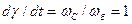 . (3.89)
. (3.89)
Тогда уравнения (3.83)-(3.85) для фазы 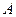 будут иметь вид
будут иметь вид
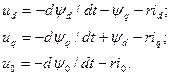 (3.90)
(3.90)
В заключение отметим, что в (3.83) и (3.84) первые слагаемые представляют собой э.д.с. трансформации, поскольку они обусловлены изменением величин соответствующих потокосцеплений, а вторые слагаемые –э.д.с. вращения. В стационарном режиме трансформаторные э.д.с., естественно, отсутствуют.
3.4.7. Выражения в операторной форме
Известно, что анализ дифференциальных уравнений упрощается, если их представить в операторной форме.
С целью упрощения записи операторных уравнений примем, что начальные условия являются нулевыми , то есть 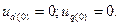
Эти условия всегда можно принять, так как по принципу наложения решение задачи можно свести к суммированию величин известного предшествующего режима с их приращениями, которые возникают от рассматриваемого возмущающего фактора.
В этой связи, при записи выражений в операторной форме будем фиксировать не полные величины, а их приращения, предшествующие значения которых равны нулю. При этом будем также иметь в виду, что 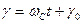 , а в относительных единицах
, а в относительных единицах 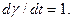
Дата добавления: 2016-04-14; просмотров: 1562;
