Приведение параметров цепи ротора к статору синхронной машины
Такое приведение позволит освободиться от магнитной связи между ротором и статором синхронной машины и представить ее соответствующей схемой замещения.
Для вывода соотношения приведения параметров ротора к статору воспользуемся спрямленной х.х.х. генератора (рис.3.15, б), проходящую через начала координат и точку с координатами ( 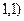 .
.
При этом получим связи:
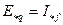 и
и 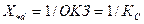 . (3.41)
. (3.41)
Зная 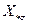 и
и  , можно построить основной реактивный треугольник, положение вершины которого фиксируется относительным током возбуждения
, можно построить основной реактивный треугольник, положение вершины которого фиксируется относительным током возбуждения 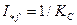 (рис.3.19).
(рис.3.19).
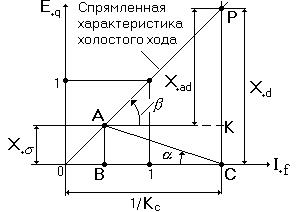
Таким образом, при этом токе возбуждения ток к.з. на выводах генератора будет равен номинально-
му. При этом положение точки 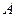 определяется ординатой, представля-
определяется ординатой, представля-
ющей собой относительную величину реактивности 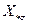 ( так как
( так как 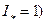 . Точка
. Точка 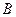 является проекцией точки
является проекцией точки 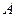 на ось тока возбуждения
на ось тока возбуждения 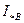 .
.
Ранее установлено, что катет 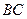
Рис.3.19. треугольника  определяет продольную реакцию, создаваемую токами трех фаз статора и тем самым позволяет на графике определить масштаб тока статора
определяет продольную реакцию, создаваемую токами трех фаз статора и тем самым позволяет на графике определить масштаб тока статора 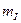 , мм.
, мм.
Таким образом 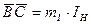 . (3.42)
. (3.42)
Допустим, что для графика рис.3.19 нами приняты масштабы:
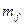 - для единицы тока возбуждения, мм;
- для единицы тока возбуждения, мм;
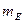 - для единицы э.д.с. статора, мм.
- для единицы э.д.с. статора, мм.
Следовательно, для единицы реактивности можно определить масштаб как 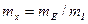 , мм.
, мм.
Выразим ток возбуждения в масштабе тока статора: 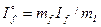 .
.
Согласно рис.3.19 можно записать
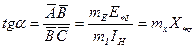 ; (3.43)
; (3.43)
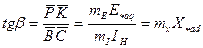 . (3.44)
. (3.44)
Из диаграммы рис.3.19 имеем
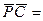
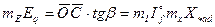 =
= 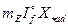 ; или
; или 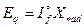 . (3.45)
. (3.45)
В соответствии с принятым спрямлением х.х.х. то есть с учетом (3.41)
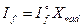 , (3.46)
, (3.46)
то есть истинное и приведенное к статору значения тока возбуждения связаны постоянным (при принятом допущении) коэффициентом пропорциональности, равным 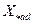 .
.
Для обеспечения обратимости взаимоиндукции между трехфазной обмоткой статора и одноосной обмоткой возбуждения при выражении величин ротора и статора в системе относительных единиц, следует принять на стороне обмотки возбуждения в качестве базисных условий: 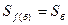 , то есть ту же базисную мощность, что и на стороне статора; базисный ток
, то есть ту же базисную мощность, что и на стороне статора; базисный ток 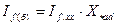 , базисное напряжение
, базисное напряжение 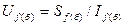 .
.
После того, как все величины цепи обмотки возбуждения будут выражены в относительных единицах при указанных базисных условиях, они одновременно становятся приведенными к статору. Согласованную таким образом систему относительных единиц статора и ротора называют взаимной системой относительных единиц.
3.3.2. Переходные э.д.с. и реактивности синхронной машины
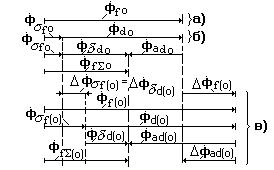 |
Рассмотрим баланс магнитных потоков в продольной оси ротора синхронной машины в установившемся симметричном режиме ее работы с остающим по фазе током (рис.3.20).
Рис.3.20.
Дата добавления: 2016-04-14; просмотров: 1357;
