А- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима 1 страница

При отсутствии насыщения мащшины каждый из ее магнитных потоков и их отдельные составляющие можно рассматривать независимо друг от друга.

Рассмотрим баланс магнитных потоков в синхронной машине по продольной оси при разных режимах:

а) при холостом ходе полный магнитный поток обмотки возбуждения 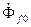состоит из потока рассеяния 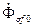и полезного потока 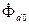, достигающего обмотки статора (рис.3.20., );

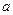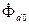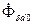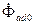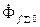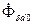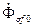б) при нагруженной машине в установившемся режиме полезный поток является уже геометрической разностью продольного потока в возду-шном зазоре и встречно ему направленного потока реакции статора . Результирующий магнитный поток , сцепленный с обмоткой возбуждения равен сумме и (рис.3.20, );

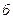в) при внезапном набросе нагрузки во внешней сети ток статора увеличится и, как следствие, увеличится поток продольной реакции статора на 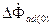. В соответствии с правилом Ленца приращение потока 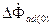вызовет ответную реакцию обмотки возбуждения 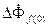. Исходя из принципа неиз-

менности потокосцепления машины в начальный момент переходного про-

цесса, приращения потокосцеплени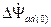й и 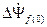должны компенсиро-

вать друг друга, то есть

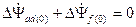, (3.47)

или в относительных единицах

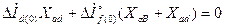. (3.48)

Из (3.48) следует, что приращения токов статора 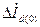и ротора 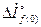связаны между собой простым соотношением и различие их обусловлено только реактивностью рассеяния обмотки возбуждения .

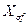В ненасыщенной машине поток 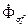составляет некоторую постоянную долю 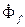, которая определяется коэффициентом рассеяния обмотки возбуждения

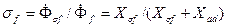. (3.49)

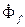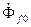С увеличением от до 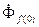пропорционально ему увеличивается поток рассеяния от 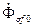до 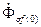, что приводит к уменьшению потока 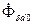до 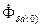.Однако результирующий поток 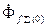, сцепленный с обмоткой возбуждения, сохраняет свое предшествующее значение 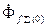(рис.3.20, ).

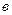Для нахождения э.д.с. статора синхронной машины в начальный момент нарушения режима воспользуемся неизменностью потока 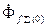, сцепленно-

го с обмоткой возбуждения.

Зная коэффициент рассеяния обмотки возбуждения 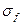, определим ту часть магнитного потока 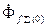, которая связана со статором, то есть

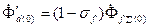. (3.50)

При этом можно утверждать, что потокосцепление 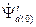(соответствующее магнитному потоку 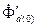) и соответствующая ему э.д.с. 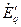в обмотке стато-

ра сохраняют в начальный момент переходного процесса свои предшеству-

ющие значения.

Раскроем выражение (3.50), опуская индекс ( ):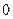

= =

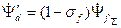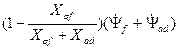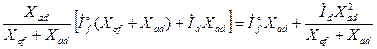. (3.51)

Сопоставляя выражения (3.46) и (3.51) и учитывая, что потокосцеплению 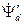соответствует наводимая в обмотке статора э.д.с. 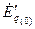и все величины выражены в относительных единицах, можно записать: 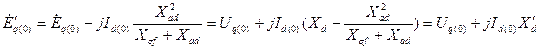. (3.52)

Э.д.с. 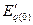называют поперечной переходной э.д.с., а реактивность 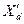-продольной переходной реактивностью, величина которой указывается заводом-изготовителем.

Покажем рассмотренные величины на векторной диаграмме токов и напряжений явнополюсной синхронной машины для начального момента нарушения режима, работающей с отстающим током (рис.3.21)(опуская индекс “ ”).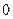

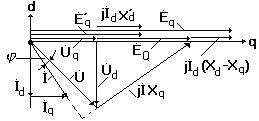Рис.3.21.

Схематично порядок построения может быть таким:

.

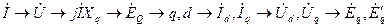Оставаясь неизменной в начальный момент внезапного нарушения режи-

ма, переходная э.д.с. 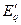позволяет связать параметры предшествующего ре-

жима с параметрами нового режима (наступившего от внезапного измене-

ния).

В этом и состоит практичекая ценность 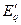. С этой точки зрения термин ”переходная” нужно понимать так, что эта э.д.с. вместе с 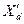позволяет оценить количественно внезапный переход от одного режима к другому. Следует отметить, что э.д.с. 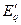нельзя измерить (ибо ее значение опреде-

ляется по параметрам предшествующего режимa). Поэтому эту э.д.с. нередко называют расчетной или условной.

Придадим выражению 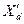иной вид, введя в него коэффициент рассеяния 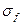: 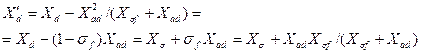. (3.53)

Из структуры выражения (3.53) непосредственно следует, что реактив-

ность 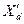представляет собой результирующую реактивность статорной обмотки при закороченной обмотке возбуждения (рис.3.22). Причем э.д.с.

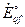, соответствующая результирующему потокосцепления обмотки возбуждения 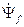_S должна быть введена в схему последовательно с .

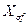После замены ветве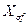й и 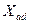одной эквивалентной, получим схему замещения рис.3.22, в, в которой машина представлена своим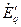и и .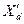

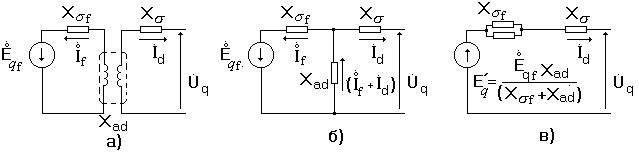
Рис.3.22.

а-исходная принципиальная схема;

б и в – схемы замещения

В связи с отсутствием у ротора в поперечной оси замкнутых контуров поток поперечной реакции статора 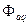при переходных процессах может изменяться беспрепятственно ( так как отсутствие замкнутых контуров исключает магнитнгое взимодействие). Поэтому внезапное изменение поперечной реакции статора 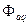(от составляющей 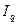полного тока стато-

ра) учитывают как падение напряженгия от тока 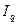в реактивности 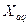. Таким образом, у такой машины переходная э.д.с. по продольной оси 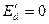, а переходное сопротивление по поперечной оси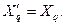

3.3.3. Сверхпереходные э.д.с. и реактивности синхронной машины

Рассмотрим синхронную машину, ротор которой имеет допольнительные (демпферные) короткозамкнутые обмотки на роторе по его обеим осям (рис.3.23).

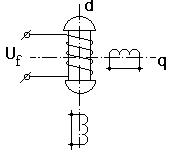Аналогично предыдущему определим э.д.с. и реактивности, которыми можно характеризовать в начальный момент переходного процесса такую машину.

Заметим, что наличие демпферных обмоток по обеим осям ротора все равно не обеспечивает его магнитную симметрию, что вынуждает определять параметры синхронной машины отдельно в продоль-

Рис.3.23. ной и поперечной осях ротора.

Для простоты анализа примем, что все величины выражены в относительных единицах, величины ротора приведены к статору и обе обмотки ротора в его продольной оси (возбуждения и демпферная) связаны между собой общим потоком взаимоиндукции 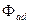, который обусловливает реактивность продольной реакции статора .

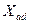В такой машине внезапное изменение потока 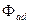вызовет ответную реакцию ротора по оси 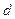, которая образуется из приращения магнитного потока обмотки возбуждения 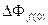и приращения магнитного потока продольной демпферной обмотки 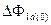(здесь 1 указывает номер обмотки, индекс 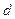-расположение по оси ).

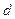При внезапном изменении потока 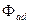должен сохраниться в начальный момент баланс результирующих потоков (потокосцеплений), сцепленных с обмотками статора, возбуждения и продольной демпферной по оси 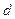, то есть должны быть соблюдены следующие равенства:

а) для обмотки возбуждения

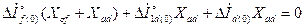; (3.54)

б) для продольной демпферной обмотки

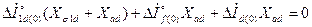, (3.55)

где 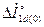, 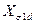-приведенный к статору начальный ток, наведенный в продольной демпферной обмотке, и ее реактивность рассеяния.

Приравняв левые части (3.54) и 3.55), получим

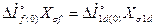, (3.56)

откуда видно, что чем меньше рассеяние соответствующей обмотки, тем больше наведенный в ней ток и тем, соответственно, больше ее участие в создании ответной реакции ротора. Также очевидно, что наличие демпфер-

ной обмотки по оси 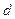обусловливает более полную компенсацию продоль-

ного магнитного потока от внезапного приращения потока реакции статора 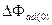и частично разгружает обмотку возбуждения в участии ответной реакции.

Заменим совместную ответную реакцию обмотки возбуждения и продоль-

ной демпферной обмотки в начальный момент переходного процесса реакцией от суммарного тока 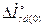= 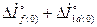, протекающего в одной эквивалентной обмотке по продольной оси ротора с реактивностью рассеяния 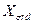, то есть

.

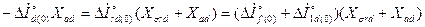Далее, используя (3.54) и (3.56), приведем последнее равенство к виду

,

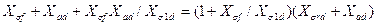откуда найдем 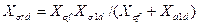. (3.57)

Таким образом, реактивность рассеяния эквивалентной обмотки в продольной оси ротора можно найти как результирующую реактивность двух параллельных ветвей с 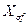и .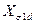

Следовательно, для получения реактивности в продольной оси при нали-

чии на роторе одной демпферной обмотки по оси 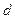, характеризующей ма-

шину в начальный момент внезапного нарушения режима, достаточно в вы-

ражение для 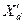вместо 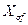ввести выражение для 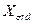, определив тем самым продольную сверхпереходную реактивность.

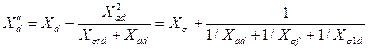. (3.58)

В поперечной оси ротора, где расположена только одна демпферная обмотка по аналогии с выкладками при определении 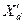можно найти так называемую поперечную сверхпереходную реактивность, характеризую-щую машину в начальный момент внезапного нарушения режима по попе-

речной оси.

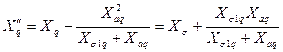. (3.59)

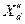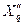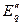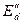Э.д.с. за реактивностями и называют сверхпереходными э.д.с. и , соответственно, в продольной и поперечной осях . Эти э.д.с., как и э.д.с. 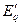, сохраняют свои значения неизменными в начальный момент внезапного нарушения режима. Их величины находят из очевидных равенств: 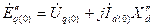; 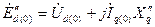. (3.60)

На рис.3.24 приведена векторная диаграмма токов и напряжений и э.д.с. в начальный момент нарушения режима для явнополюсной синхронной ма-

кая индекс “0”).

Рис.3.24.

Схематично порядок построения может быть следующим:

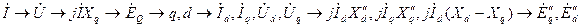Как и переходная э.д.с. 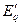, сверхпереходные э.д.с. 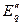, 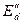и 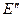являются расчетными условными величинами.

Модуль 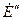может быть найден из соотношения .

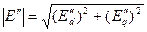Таким образом, для машины с демпферными обмотками реактивност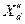и и 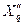вместе с э.д.с. 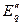и 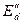позволяют перейти от одного режима, изменившегося скачком, к другому. Приставка “сверх” в термине “сверхпереходные” указывает на то, что данные параметры и величины учитывают влияние демпферных обмоток ротора.

Реактивност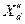и и 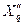являются характерными параметрами машины и обычно задаются в справочниках.

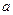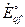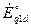Три магнитосязанные обмотки в продольной оси (статора, возбуждения, демпферная) могут быть представлены эквивалентной схемой замещения (рис.3.25, ), как для трехобмоточного трансформатора. Здесь э.д.с. и соответствуют результирующим потокосцеплениям обмотки возбуждения и продольной демпферной обмотки. Упрощение этой схемы приводит к 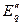и 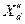(рис.3.25, ).

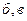В поперечной си ротора, где имеется магнитная связь между обмоткой статора и поперечной демпферной обмоткой (рис.3.26, а), схема замещения будет той же, что и для двухобмоточного трансформатора, после упрощения которой можно получить 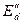и 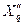(рис.3.26, , ).

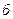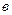Полученные схемы замещения машины по осям 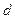и 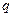наглядно показывают взаимную связь между приведенными к статору токами отдельных обмоток.

При отсутствии в них активных сопротивлений они отражают только начальный момент переходного процесса.

Рис.3.25.

а- исходная принципиальная схема;

б и в- схемы замещения

Рис.3.26.

а- исходная принципиальная схема;

б и в- схемы замещения

3.3.5. Сравнение э.д.с. и реактивностей синхронной машины

Из схем замещения для реактивностей синхронной машины (рис.3.27) получаем следующие соотношения:

; ; .

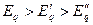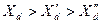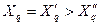Попытаемся дополнить и пояснить полученные соотношения из следующих физических соображений.

Магнитный поток, создаваемый током статора 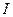в установившемся режиме, частично замыкается по путям рассеяния статорной обмотки ( 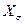), а основная его часть, пройдя через воздушный зазор, замыкается через полюсы и массив ротора ( 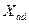и 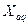). В этих условиях сопротивление для магнитного потока невелико и индуктивности машины, характеризующая величину магнитного потока на единицу намагничивающей сила, максимальны.

При внезапном изменении магнитного потока статора на 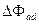в обмотке возбуждения согласно правилу Ленца наводится ток, создающий встречный магнитный поток, который вытесняет магнитный поток статора из тела ротора. Таким образом, при том же возбуждении, что было ранее, при той же намагничивающей силе статора в этих условиях создается меньший магнитный поток, что и обусловливает соответственно меньшую величину переходной реактивности 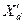по сравнению с реактивностью .

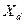Очевидно, чем больше будет на роторе замкнутых обмоток, тем меньшая часть магнитного потока статора сможет проникнуть в тело ротора в начальный момент переходного процесса. В пределе, когда весь магнитный поток статора будет вытеснен из тела ротора, реактивность машины в переходном процессе будет минимальной и равной .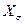

Аналогично можно объяснить разницу в реактивностях синхронной машины по поперечной оси.

по продольной оси

по поперечной оси

Рис.3.27.

3.3.5.Характеристики двигателей и нагрузки

Изложенные выше полученные результаты в равной степени относятся как к синхронным генераторам, так и к синхронным двигателям и компенсаторам.

Обратимся теперь к асинхронным двигателям. Проведенный анализ показал [2], что асинхронный двигатель в начале переходного процесса можно рассматривать как невозбужденный синхронный двигатель.

Следовательно, в начальный момент нарушения режима для асинхронно-

го двигателя можно определить сверхпереходные реактивность и э.д.с.

Благодаря полной симметрии ротора, здесь отпадает необходимость разложения величин по отдельным осям.

Сверхпереходная реактивность двигателя может быть получена из его схемы замещения, которая аналогична схеме рис. 3.25, в. Непосредственно из этой схемы замещения следует, что сверхпереходная реактивность асинхронного двигателя 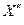представляет собой реактивность короткого замыкания (то есть когда двигатель заторможен). Относительную величину этой реактивности на практике определяют как

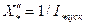, (3.61)

где 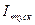- относительный пусковой ток двигателя (при пуске без реостата).

Начальное значение сверхпереходной э.д.с. 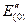двигателя определяют по параметрам предшествующего режима в соответствии с векторной диаграммой рис. 3.28.

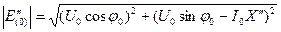, (3.62)

или приближенно, если принять э.д.с. 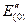, равной проекции вектора этой э.д.с. на вектор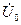

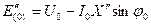, (3.62, а)

где 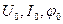- модули предшествующего напряжения, тока и угла сдвига между их векторами.

В практических расчетах начального момента переходного процесса обычно учитывают отдельно лишь крупные двигатели, которые могут оказать существенное влияние на процесс. Все остальные двигатели вместе с другими электроприемниками целесообразно учитывать в виде обобщенных нагрузок

крупных узлов энергосистемы, характеризуя такие нагрузки средними параметрами.

Установлено, что в начальный момент переходного процесса обобщенную нагрузку можно приближенно характеризовать следующими параметрам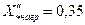и: и 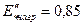, считая их выраженными в относительных ...Рис.3.28. единицах при полной рабочей мощности (в МВА) нагрузки и среднем номинальном напряжении той ступени где она присоединена.

3.3.6. Практический метод расчета

начального сверхпереходного и ударного токов

После определения параметров, которыми характеризуются все элементы электрической системы в момент внезапного нарушения режима вычисление начального сверхпереходного тока не вызывает принципиальных затруднений.

Однако, в практических расчетах с целью упрощения принимают

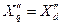, что позволяет отказаться от разложения величин на составляющие по осям 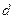и 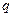, а величину сверхпереходной э.д.с. генератора определять по выражениям