Дифракция световых волн: принцип Гюйгенса-Френеля 1 страница
Дифракцией называется совокупность явлений, наблюдаемых при распространении в среде с резкиминеоднородностямии связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнамипрепятствийи проникновению света в область геометрической тени. Отклонения от законов геометрической оптикипри прочих равных условиях оказываются тем меньше, чем меньше длина волны. Между интерференциейи дифракциейнет существенного физического различия. Оба явления заключаются в перераспределении светового потокав результате суперпозициисветовых волн.
Перераспределение интенсивности, возникающее в результате суперпозициисветовых волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией световых волн.
Перераспределение интенсивности, возникающее вследствие суперпозиции световых волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракциейсветовых волн. Поэтому говорят об интерференционной картинеот двух узких щелей и о дифракционной картине от однойщели. Согласно принципу Гюйгенса - Френелякаждый (рис. 10.15) элемент dS волновой поверхностиS площадью служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS площадью. Амплитуда dA колебаний A светового вектора
сферической(10.9)световой волны с учётом расстояния r от элемента dS площадьюисточника сферической световойволны до произвольной М точки пространства имеет следующий вид: dA = ma0 dS/r, (10.79) где m - коэффициент, зависящий от υ угла между нормалью n к элементу dS площадью и r радиусом - вектором, который соединяет этот элемент dS площадью с произвольной М точкой пространства. При υ = 0 этот m коэффициентмаксимален. При υ = π/2 коэффициент m обращается в нуль. От каждого (рис. 10.15) элемента dS площадьюволновой поверхностиS площадью в
|

находящейсяна расстояния r от элемента dS площадьюисточника сферической световойволны в направлении υ угла между n нормалью к этому элементу dS площадью; Ф = ωt + φ0 - фазаколебания в произвольный момент t времени на сферическойволновой поверхности S площадью; a0 - множитель, определяемый амплитудойсветовой волны в том месте, где находится элемент dS площадьюнаволновойповерхностиS площадью; φ0 - начальная фазаколебания сферической световойволны в момент t0 = 0 временив месте расположения волновойповерхностиS площадью; ω -циклическая частотаколебаний A светового вектора сферической световойволны; k = ω/v - волновое число;
v = 1/(ε0εμ0μ)1/2 - фазовая скорость электромагнитнойволны, чем являются световые волны с λ0 длинами волнв вакууме,находящимися в интервале (10.3) 10 нм < λ0 < 1 мм и распространяющимися в среде с постоянными ε диэлектрической и μмагнитной проницаемостями. Аналитическое выражение принципа Гюйгенса - Френелязаключается в том, что результирующаяпроекция Aна плоскость, перпендикулярную r радиусу- вектору,A светового вектора сферической световой волны (рис. 10.15) в произвольной М точке пространства, представляет собой следующую суперпозициюпроекций (10.79) dA от всех элементов dS площадьюволновойповерхностиS площадью: A = ∫dA = ∫(ma0/r)cos(ωt - kr + φ0)dS. (10.81) S S
Дифракция световых волн: метод зон Френеля
Точечный источник S создаёт монохроматическую сферическую световую волну в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ= λ0 /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.16.
|
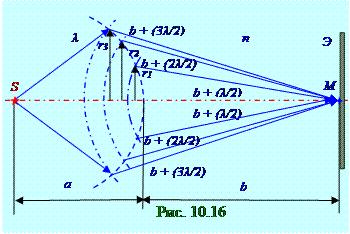
Если в M точку пространства на Э экране будут приходитьсветовые волны от m - зон с
r1, r2, r3, … радиусами, то результирующая АамплитудаA светового вектора сферической световой волны в этой M точке пространства будет равна алгебраическойсумме А1, А3, А5, … амплитуд, т.е. от зон с нечётныминомерамиr1, r3, r5, … радиусов и А2, А4, А6, … амплитуд, т.е. от зон с чётныминомерами r2, r4, r6, … радиусов.
Все световые волны в M точке пространства от зон с нечётныминомерамиr1, r3, r5, …радиусовприходят в точку пространства вфазе, т.к. они проходят b + λ/2, b + 3λ/2, b + 5λ/2, …оптические пути, т.е. отличающиеся на λдлину волны. Примем знак их А1, А3, А5, …амплитудположительным. Все световые волны от зон с чётныминомерамиr2, r4, r6, … радиусовприходят в M точку пространства в фазе, т.к. они проходят b +2λ/2, b +4λ/2, b + 6λ/2, …оптические пути, т.е. отличающиеся на λдлину волны. Но А2, А4, А6, … амплитуды от зон с чётныминомерамиr2, r4, r6, … радиусовпротивоположны по фазе А1, А3, А5, …амплитудам, т.е. от зон с нечётныминомерамиr1, r3, r5, … радиусов. Поэтому знак А2, А4, А6, … амплитудявляетсяотрицательным.
Результирующая А амплитудаA светового вектора сферической световой волны в M точке пространства (рис. 10.16) на Э экране от зон с нечётныминомерамиr1, r3, r5, …радиусови от зон с чётныминомерамиr2, r4, r6, … радиусовимеет следующий вид:
А = А1 - А2 + А3 - А4 + … = (А1/2) + [(А1/2) - А2 + (А3/2)] +[(А3/2) - А4 + (А5/2)] + … (10.82) В (10.82) слагаемые, являющиеся суммой АамплитудA светового вектора сферической световойволны в M точке пространства (рис. 10.16) от соседнихзон с нечётныминомерамирадиусови от зон с чётныминомерамирадиусов,имеют следующий вид:
(А1/2) - А2 + (А3/2) ≈ 0, (А3/2) - А4 + (А5/2) ≈ 0, (А5/2) - А6 + (А7/2) ≈ 0, …, (10.83) т.к. А1, А3, А5, … амплитуды, т.е. от зон с нечётныминомерамиr1, r3, r5, … радиусов, примерно равныА2, А4, А6, … амплитудам от зон с соседними чётныминомерамиr2, r4, r6, …. радиусов.
Подставляем (10.83) в (10.82): А = А1 - А2 + А3 - А4 + … ≈ А1/2, (10.84) из чего следует, что при открытииm - зонФренелярезультирующая А амплитудаA светового вектора сферической световой волны в M точке пространства будет меньше амплитуды А1 при открытой только 1 - ой зонес r1 радиусом.
При нечётномколичествеоткрытыхзонФренеля, например m = 3,результирующая А амплитудаA светового вектора сферической световой волны в M точке пространства c учётом (10.83) имеет следующий вид:
А = А1 - А2 + А3 = (А1/2) + [(А1/2) - А2 + (А3/2)] + А3/2 ≈ (А1/2) + (А3/2) > А1/2. (10.85) При произвольномнечётном m количествеоткрытыхзонФренелярезультирующая А амплитудаA светового вектора сферической световой волны в M точке пространства c учётом (10.83) имеет следующий вид: А ≈ (А1/2) + (Аm /2). (10.86)
При чётномколичествеоткрытыхзонФренеля, например m = 4,результирующая
А амплитудаA светового вектора сферической световой волны в M точке пространства c учётом (10.83) имеет следующий вид:
А = А1 - А2 + А3 - А4 = (А1/2) + [(А1/2) - А2 + (А3/2)] +[(А3/2) - А4] ≈ (А1/2) + (А3/2) - А4 < А1/2.(10.87) При произвольном mчётномколичествеоткрытыхзонФренеля результирующая
А амплитудаA светового вектора сферической световой волны в M точке пространства c учётом (10.83) имеет следующий вид: А ≈ (А1/2) + (Аm-1 /2) - Аm.(10.88) Амплитуда Аm-1 светового A вектора сферической световой волны в M точке пространства в (10.88) от зоны с нечётнымномеромrm-1 радиусапримерно равнаАm амплитуде от зоны с соседним чётнымномеромrm радиуса, поэтому имеет место следующее выражение: (Аm-1 /2) - Аm ≈ - Аm/2.(10.89) Подставляем (10.89) в (10.88) иполучаемследующую А результирующую амплитуду
A светового вектора сферической световой волны в M точке пространства при произвольномчётном m количествеоткрытыхзонФренеля: А ≈ А1/2 - Аm/2. (10.90) Сравниваем (10.86) и (10.90), объединяем их в одно выражение и получаем следующую
Арезультирующую амплитудуA светового вектора сферической световой волны в M точке пространства при произвольномm количествеоткрытыхзонФренеля: А ≈ А1/2 ± Аm/2, (10.91) где знак "+" берётся при нечётном количествеоткрытыхзонФренеля, а знак "-" берётся причётномколичествеоткрытыхзонФренеля.
Дифракция световых волн: радиус зон Френеля
|
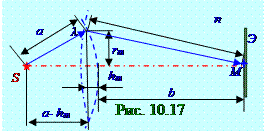
 Радиус (рис. 10.16) rm зоныФренеляявляетсякатетомдвух прямоугольных (рис. 10.7) треугольников. Исключением rm2 определяем следующую высоту hm сферического сегментаm -ой зоныФренелянасферическойволновой поверхности(рис. 10.17): rm2 = a2 - (a - hm)2
Радиус (рис. 10.16) rm зоныФренеляявляетсякатетомдвух прямоугольных (рис. 10.7) треугольников. Исключением rm2 определяем следующую высоту hm сферического сегментаm -ой зоныФренелянасферическойволновой поверхности(рис. 10.17): rm2 = a2 - (a - hm)2
rm2 = (b + mλ/2)2 - (b + hm)2 ↔
↔ hm = [bmλ + m2(λ/2)2] /2(a + b). (10.92) Ограничившись рассмотрением не слишком больших номеровm зонФренеля, можно ввиду малости λдлинысветовой волны пренебречь в (10.92) слагаемым, содержащим λ2: hm ≈ bmλ /2(a + b).(10.93)
|
|
Подставляем (10.93) высоту hm сферического сегментаm - ой зоныФренелянасферическойволновой поверхности(рис. 10.17) в (10.94), в результате чего в зависимости от a радиусасферическойволновой поверхности в произвольный момент tвремени, расстояния a + b от Sисточникасветовой волны до Э экрана, b расстояния от центрасферическойволновой поверхности до (рис. 10.16),
(рис. 10.17) произвольной М точки пространства, m номераинтересующей открытойзоныФренеля и длины λ = λ0 /n световой волны в однородной изотропной среде с n показателем преломления получаем следующее выражениеrmрадиуса зоныФренеля: m = (abmλ/a+b)1/2. (10.95)
Применение метода зон Френеля в дифракции световых волн от круглого диска: пятно Пуассона
|

номерами r1, r2, r3, … rm радиусов, результирующая АамплитудаA светового вектора сферическойсветовой волны в M точке пространства (рис. 10.16) от (10.84) всех открытых зон с
m + 1, m + 2, m + 3, …номерами, т.е. от зон с rm+1, rm+2, rm+3…номерамирадиусов, имеет следующий вид: А = Аm+1 - Аm+2 + Аm+3 - Аm+ 4 + … =
= (Аm+1 /2) + [(Аm+1/2) - Аm+2 + (Аm+3/2)] + [( Аm+3 /2) - Аm+4 + (Аm+5 /2)] +… (10.96) В (10.96) слагаемые: (Аm+1/2) - Аm+2 + (Аm+3/2) ≈ 0, ( Аm+3 /2) - Аm+4 + (Аm+5 /2) ≈ 0, …, (10.97) т.к. амплитуды Аm+1, Аm+3, т.е. от зон с номерамиr m+1, r m+3 радиусов, примерно равны
А m+2 амплитуде зоны с соседнимномером r m+2радиуса, а Аm+3, Аm+5 амплитуды, т.е. от зон с номерамиr m+3, r m+5 радиусов, примерно равныА m+4 амплитуде зоны с соседнимномеромr m+4 радиуса и т.д. Подставляем (10.97) в (10.96) и получаем следующее выражение Арезультирующей амплитудыA светового вектора сферическойсветовой волны в M точке пространства (рис. 10.16) от всех открытых зон с m + 1, m + 2, m + 3, …номерами,т.е. от зон с номерамиrm+1, rm+2, rm+3…радиусов: А ≈ Аm+1 /2. (10.98) Согласно (10.98) за непрозрачным(рис. 10.18) Д дискомобразуетсясветлоепятно, которое назвали пятном Пуассона и которое тем светлее, чем меньше зон mФренеляперекроет этотнепрозрачный Д диск, т.к. с уменьшением m количества зон Френеля, перекрытыхнепрозрачным
Д диском, уменьшается rmрадиус (рис. 10.16)зоныФренеля и увеличивается, (10.9) вследствие уменьшения расстояния r от источникасферической световойволны до произвольной M точки пространства на Э экране, Аm+1амплитудаA светового вектора сферическойсветовой волны в этой
M точке пространства.
Графический метод расчёта дифракции световых волн от круглого отверстия с помощью спирали Френеля
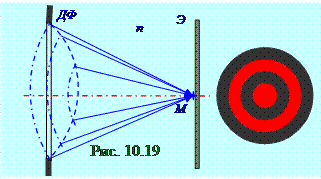
При дифракцииФренеля на круглом отверстиипри открытии ДФдиафрагмой нечётногоколичества, например (рис. 10.19), 3 - х зонна Э экране возникают светлыеи тёмныедифракционные кольцасо светлым(10.86)пятномв центре.
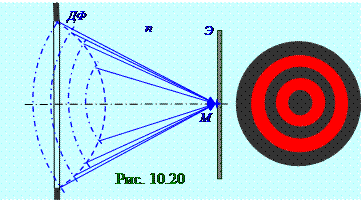
При дифракцииФренеля на кругломотверстиипри открытии ДФдиафрагмойчётногоколичества, например (рис. 10.20), 4 - х зон на Э экране возникают светлыеи тёмныекольцас тёмным(10.90)пятномв центре. Дифракция Френеля существует при сферическойволновой поверхностисветовой волны. Если источник сферическойсветовой волны, например, Солнце, находится далеко от преградыили диафрагмы, то после её прохождения формируется параллельныйпучок света с площадью сечения, равного по форме и величине площади диафрагмы.
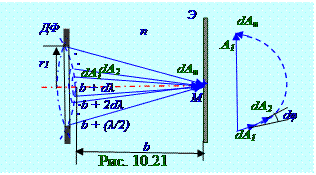
В M точку пространства на Э экране (рис. 10.21) приходятсветовые волны от одной зоны Френеля с r1 радиусом. Результирующий (рис. 10.3) вектор A1 амплитудыA светового вектора сферической световой волны в M точке пространства на Э экране от одной зоны Френеля с r1 радиусом будет равен сумме элементарных векторов dA1, dA2, …, dAn от каждой узкойкольцевой зоны, находящихся на расстояниях соответственно b + dλ, b + 2dλ, …, b + (λ/2) до этой M точки пространства на Э экране. Модули (рис. 10.21) dA1, dA2, …, dAn элементарных dA1, dA2, …, dAn векторовот каждой узкойкольцевой зоны убываютпо величине, поскольку по мере удаления кольцевой зоны от одной зоны Френеля увеличивается расстояние от этой кольцевой зоны до M точки пространства на Э экране.
|
электромагнитной волны, чем являются световые волны с λ0 длинами волнв вакууме,находящимися в интервале (10.3) 10 нм < λ0 < 1 мм и распространяющимисяв однородной изотропной среде с постоянными ε диэлектрической и μмагнитной проницаемостями.
Световая волна приходит в M точку пространства на Э экране от узкойкольцевой зоны с элементарным вектором dA1 (10.25) с фазой, имеющей следующий вид: Ф1 = ωt - k(b + dλ). (10.100)
Разность Ф2 - Ф1 фаз у световых волн, пришедших соответственно от узкихкольцевых зон с элементарными векторами dA2, dA1 с учётом (10.100), (10.99) имеет следующий вид:
Ф2 - Ф1 = kdλ = 2πdλ/λ = dφ,(10.101) где dφ - угол (рис. 10.21) между векторами от соседних узкихкольцевых зон.
Световая волна приходит в M точку пространства на Э экране от узкойкольцевой зоны с элементарным вектором dAn(10.25), прилегающей к (рис. 10.21) границе первой зоныФренеля с фазой, имеющей следующий вид: Фn = ωt - k [b + (λ/2)]. (10.102)
Разность Фn - Ф1 фаз у световых волн, пришедших соответственно от узкихкольцевых зон с элементарными векторами dAn, dA1 с учётом (10.102), (10.101) имеет следующий вид: Фn - Ф1 = k(λ/2 - dλ) ≈ 2πλ/2λ = π, (10.103)
поэтому (рис. 10.21) элементарный вектор dAnот узкойкольцевой зоны, прилегающей к границе первой зоны Френеля, направлен противоположно элементарному вектору dA1 от узкойкольцевой зоны, находящейся в центре первой зоны Френеля.
Таким образом, модули (рис. 10.21) dA1, dA2, …, dAn элементарных векторов dA1, dA2, …, dAn от каждой узкойкольцевой зоны убываютпо величине, а dφ угол между векторами от соседних узкихкольцевых зон постоянен. По этой причине фигура, составленная из соседних векторов dA1, dA2, …, dAn от каждой узкойкольцевой зоны, являющихся элементом зон Френеля, представляет собой закручивающуюсяспираль с постепенным уменьшением радиуса этой спирали по мере увеличения количества зон Френеля.
В M точку пространства на Э экране (рис. 10.22) приходятсветовые волны от полутора зон Френеля с r1,5 радиусом. Результирующий (рис. 10.22) вектор A1,5 амплитудыA светового вектора сферической световой волны в M точке пространства от полутора зон Френеля с r1,5 радиусом будет равен сумме элементарных векторов dA1, dA2, …, dAn от каждой узкойкольцевой зоны, находящихся на расстояниях соответственно b + dλ, b + 2dλ, …, b + (3λ/4) до этой M точки пространства на Э экране.
|
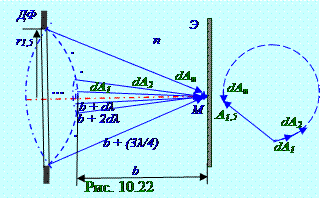
поэтому (рис. 10.22) элементарный вектор dAnот узкойкольцевой зоны, прилегающей к границе полуторной зоны Френеля, составляет с элементарным вектором dA1 от узкойкольцевой зоны, находящейся в центре первой зоны Френеля, 3π/2 угол.
|
|
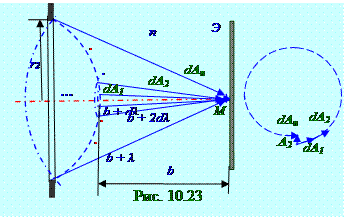
узкойкольцевой зоны, прилегающей к границе второй зоны Френеля, составляет с элементарным вектором dA1 от узкойкольцевой зоны, находящейся в центре первой зоны Френеля, 2π угол, т.е. элементарный вектор dAnот узкойкольцевой зоны, прилегающей к границе второй зоны Френеля, сонаправлен элементарному вектору dA1 от узкойкольцевой зоны, находящейся в центре первой зоны Френеля.
Дата добавления: 2016-02-14; просмотров: 873;
