Высшие волны коаксиала и одноволновый режим

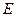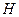Перейдем к - и -волнам. В этих случаях квазистатический принцип не действует и необходимо решать уравнения Гельмгольца (13.2.2) в соответствующих граничных условиях. Зависимость от 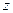дается равенствами (13.2.3), поперечные составляющие векторов 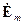и 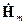выражаются через продольные составляющие 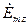, , 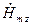а двумерная краевая задача в сечении линии (13.2.4) в полярных координатах сечения принимает вид:

,

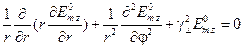(13.8.6)

и аналогичное уравнение для 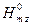. Эта задача решается методом разделения переменных при надлежащих граничных условиях на внешней поверхности внутреннего проводника и внутренней поверхности внешнего проводника. Решение выражается через функции Бесселя 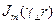и Неймана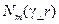 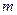-го порядка и их первые производные.

Из граничных условий для 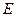-волн: 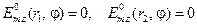можно вывести уравнение относительно 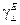[13.1, 13.3]:

,

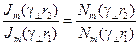(13.8.7)

а из граничных условий для 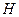-волн – уравнение для :

.

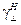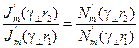(13.8.8)

Эти уравнения трансцендентны и решаются численными методами. Анализ уравнений (13.8.7), (13.8.8) показывает, что при любом соотношени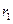и и 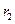первым высшим типом в коаксиале является волна 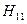. Критическая длина волны для этого типа зависит от отношения 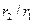. Асимптотический анализ уравнения (13.8.8) показывает, что при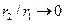 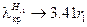, а при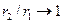 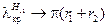. Обычно в качестве независимого от отношения 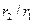значения критической длины волны приближенно принимают последний результат:

,

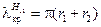(13.8.9)

при этом ошибка этого равенства во всем диапазоне отношений 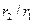не превышает 10%.

Таким образом, поскольку 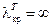, одноволновый режим в коаксиале будет для волн с длиной

.

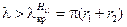(13.8.10)