Координата в линии передачи. В качестве модели эквивалентной ЛП рассмотрим двухпроводную длинную линию (рис
В качестве модели эквивалентной ЛП рассмотрим двухпроводную длинную линию (рис. 12.1.1), к которой подключен генератор монохроматического излучения круговой частоты 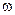 , с нагрузкой
, с нагрузкой 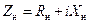 . Координату
. Координату  отсчитываем от нагрузки в сторону генератора. Пусть
отсчитываем от нагрузки в сторону генератора. Пусть 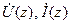 – комплексные амплитуды напряжения и тока в линии,
– комплексные амплитуды напряжения и тока в линии, 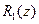 , Ом/м – погонное сопротивление,
, Ом/м – погонное сопротивление,  , 1/Ом
, 1/Ом  м – погонная проводимость,
м – погонная проводимость,  , Ф/м – погонная емкость,
, Ф/м – погонная емкость, 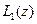 , Гн/м – погонная индуктивность линии. Далее рассматриваем регулярную эквивалентную линию, в которой погонные параметры не зависят от
, Гн/м – погонная индуктивность линии. Далее рассматриваем регулярную эквивалентную линию, в которой погонные параметры не зависят от  . Электрическая эквивалентная схема дифференциально малого участка
. Электрическая эквивалентная схема дифференциально малого участка 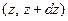 линии показана на рис. 14.2.1 (для удобства схема симметризована), стрелками показаны выбранные направления напряжения и тока.
линии показана на рис. 14.2.1 (для удобства схема симметризована), стрелками показаны выбранные направления напряжения и тока.
Телеграфные уравнения
Сопротивление, проводимость, емкость и индуктивность участка 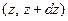 линии определяются равенствами
линии определяются равенствами
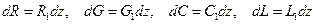 , ,
| (14.2.1) |
отсюда приращения напряжения и тока на этом участке:
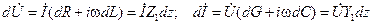 , ,
| (14.2.2) |
где 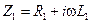 – комплексное погонное сопротивление линии;
– комплексное погонное сопротивление линии;
 – комплексная погонная проводимость линии.
– комплексная погонная проводимость линии.
Поделив равенства (14.2.2) на 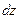 , получим телеграфные уравнения:
, получим телеграфные уравнения:
 , ,
| (14.2.3) |
определяющие связь между напряжением и током в любом сечении эквивалентной ЛП.
Уравнения Гельмгольца (волнового уравнения), коэффициент распространения
Исключим из первого уравнения ток, а из второго – напряжение. Для этого продифференцируем их по  и учтем, что в силу регулярности линии
и учтем, что в силу регулярности линии
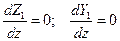 , ,
| (14.2.4) |
тогда
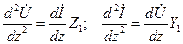 , ,
| (14.2.5) |
и подставляя в эти равенства соотношения (14.2.3), получаем волновые уравнения (уравнения Гельмгольца):
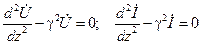 , ,
| (14.2.6) |
где
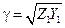 , ,
| (14.2.7) |
важный частотно-зависимый параметр эквивалентной линии – коэффициент распространения волны в линии.
Решение любого из уравнений (14.2.6) вместе с граничными условиями на концах линии полностью описывает распространение волн напряжения и тока в линии, причем достаточно решить одно из уравнений, например, для напряжения, а вторую функцию координаты  можно получить из (14.2.3).
можно получить из (14.2.3).
Падающие и отраженные волны, полное напряжение
Хотя достаточно решить одно из уравнений (14.2.6), для удобства дальнейшей интерпретации выпишем решения обоих уравнений. Общее решение однородных линейных уравнений второго порядка типа (14.2.6) хорошо известно и имеет вид:
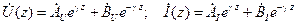 , ,
| (14.3.1) |
где 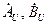 – не зависящие друг от друга произвольные постоянные размерности напряжения;
– не зависящие друг от друга произвольные постоянные размерности напряжения;
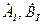 – не зависящие друг от друга произвольные постоянные размерности тока.
– не зависящие друг от друга произвольные постоянные размерности тока.
Решения волновых уравнений в виде (14.3.1) имеют весьма характерный вид: первое слагаемое в каждом решении есть падающая волна напряжения (тока), распространяющаяся от генератора к нагрузке, второе слагаемое – отраженная волна, распространяющаяся от нагрузки к генератору. Положив 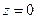 , выясняем смысл коэффициентов:
, выясняем смысл коэффициентов: 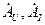 – комплексные амплитуды падающих волн напряжения и тока соответственно на (в сечении) нагрузке,
– комплексные амплитуды падающих волн напряжения и тока соответственно на (в сечении) нагрузке, 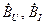 – комплексные амплитуды отраженных волн напряжения и тока соответственно на (в сечении) нагрузке. Полное напряжение (ток) на нагрузке, как следует из (14.3.1), равно сумме падающего и отраженного напряжений (токов):
– комплексные амплитуды отраженных волн напряжения и тока соответственно на (в сечении) нагрузке. Полное напряжение (ток) на нагрузке, как следует из (14.3.1), равно сумме падающего и отраженного напряжений (токов):
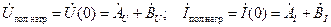 , ,
| (14.3.2) |
а равенства (14.3.1) показывают, что то же самое справедливо для любого сечения  линии: полное напряжение
линии: полное напряжение  (ток
(ток 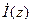 ) в любом сечении равно сумме напряжений (токов) падающей и отраженной волн напряжения (тока). Мы пришли к важному выводу: характерной особенностью эквивалентных ЛП как «длинных линий» является возможность существования в них двух волн, распространяющихся навстречу друг другу: падающей, образованной подключенным к линии генератором, и отраженной, обязанной отражению падающей волны от нагрузки; все разнообразие процессов, происходящих в ЛП, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
) в любом сечении равно сумме напряжений (токов) падающей и отраженной волн напряжения (тока). Мы пришли к важному выводу: характерной особенностью эквивалентных ЛП как «длинных линий» является возможность существования в них двух волн, распространяющихся навстречу друг другу: падающей, образованной подключенным к линии генератором, и отраженной, обязанной отражению падающей волны от нагрузки; все разнообразие процессов, происходящих в ЛП, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
Поскольку нагрузка суть пассивный элемент, амплитуды отраженных волн напряжения и тока не могут превышать амплитуд падающих волн:
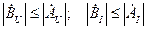 . .
| (14.3.3) |
Чтобы не возникало путаницы, заметим, что направление распространения волн определяется знаком в показателях экспонент в (14.3.1): при выборе направления оси  как на рис. 12.1.1 знак «плюс» – волна распространяется в отрицательном направлении оси
как на рис. 12.1.1 знак «плюс» – волна распространяется в отрицательном направлении оси  (падающая); «минус» – в положительном направлении оси
(падающая); «минус» – в положительном направлении оси  (отраженная). В частности, падающие волны напряжения и тока:
(отраженная). В частности, падающие волны напряжения и тока:
 , ,
| (14.3.4) |
а отраженные волны:
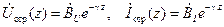 . .
| (14.3.5) |
Вторичные параметры ЭЛП (коэффициент затухания, коэффициент фазы, погонное затухание, линия без потерь, длина волны в линии, полная фаза, фазовая скорость, частотная дисперсия, волновое сопротивление)
Локальные параметры эквивалентной ЛП можно считать первичными параметрами линии. Рассмотрим теперь вторичные параметры эквивалентной ЛП, описывающие свойства распространяющихся в линии волн в целом и выражающиеся через первичные параметры. Начнем с введенного в (14.2.7) коэффициента распространения 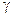 . Поскольку в общем случае
. Поскольку в общем случае 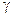 суть комплексная величина, ее можно записать в виде:
суть комплексная величина, ее можно записать в виде:
 . .
| (14.4.1) |
Действительная часть коэффициента распространения 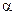 , 1/м, называется коэффициентом затухания (ослабления) волны в линии, мнимая часть
, 1/м, называется коэффициентом затухания (ослабления) волны в линии, мнимая часть  , 1/м, – коэффициентом фазы волны. Смысл этих частотно-зависимых параметров будет понятен, если записать, например, комплексную амплитуду падающей волны напряжения по (14.3.4) в виде:
, 1/м, – коэффициентом фазы волны. Смысл этих частотно-зависимых параметров будет понятен, если записать, например, комплексную амплитуду падающей волны напряжения по (14.3.4) в виде:

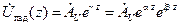 , ,
| (14.4.2) |
т. е. 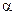 это логарифмический декремент затухания волны за счет потерь в металле и диэлектрике и, возможно, за счет потерь на излучение в сторону;
это логарифмический декремент затухания волны за счет потерь в металле и диэлектрике и, возможно, за счет потерь на излучение в сторону;  это сдвиг фазы на единицу длины линии. Если
это сдвиг фазы на единицу длины линии. Если 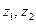 – два сечения линии, отстоящие друг от друга на 1 м, то
– два сечения линии, отстоящие друг от друга на 1 м, то
 .
.
Обычно вводят погонное затухание (ослабление):
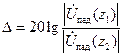 , дБ/м,
, дБ/м,
связанное с 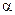 соотношением
соотношением
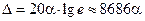 ,
,
Записав 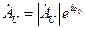 и перейдя от комплексной амплитуды к мгновенному значению, имеем:
и перейдя от комплексной амплитуды к мгновенному значению, имеем:
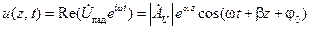 , ,
| (14.4.3) |
откуда смысл  виден еще более ясно.
виден еще более ясно.
Из (14.4.1) легко получить выражения 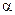 и
и  через первичные параметры линии [14.5]:
через первичные параметры линии [14.5]:
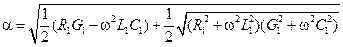 ; ;
| (14.4.4) | |
 . .
| (14.4.5) | |
В важном идеализированном частном случае отсутствия потерь (  ) из этих равенств следует:
) из этих равенств следует:
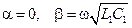 . .
| (14.4.6) |
Выражение (14.4.3) дает распределение мгновенного напряжения во времени и вдоль линии. Зафиксируем время, например, 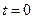 , и найдем распределение вдоль линии в случае отсутствия потерь (
, и найдем распределение вдоль линии в случае отсутствия потерь (  ):
):
 . .
| (14.4.7) |
Пространственный период этой косинусоиды
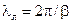
| (14.4.8) |
называется длиной волны в линии.
Аргумент косинусоиды в (14.4.3) называется полной фазой волны в линии:
 . .
| (14.4.9) |
Отсюда уравнение точек равных полных фаз  :
:
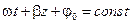 . .
| (14.4.10) |
Выражая отсюда 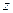 и дифференцируя по времени, получаем фазовую скорость волны частотой
и дифференцируя по времени, получаем фазовую скорость волны частотой 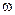 :
:
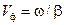 . .
| (14.4.11) |
В общем случае  зависит от
зависит от 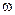 нелинейно (см. (14.4.5)) и
нелинейно (см. (14.4.5)) и 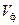 зависит от
зависит от 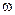 , т. е. имеет место частотная дисперсия. Однако, в идеализированном случае отсутствия потерь, как следует из (14.4.6), (14.4.11),
, т. е. имеет место частотная дисперсия. Однако, в идеализированном случае отсутствия потерь, как следует из (14.4.6), (14.4.11),
|
Из электродинамики известно [14.1, 14.5], что 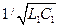 равно скорости света в той диэлектрической среде без потерь с относительными проницаемостями
равно скорости света в той диэлектрической среде без потерь с относительными проницаемостями  , которая заполняет линию передачи. В свою очередь, эта скорость равна
, которая заполняет линию передачи. В свою очередь, эта скорость равна 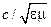 . Таким образом, в линии без потерь скорость распространения волны
. Таким образом, в линии без потерь скорость распространения волны 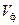 такая же, как скорость распространения в неограниченном диэлектрике с теми же
такая же, как скорость распространения в неограниченном диэлектрике с теми же  :
:
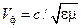 , ,
| (14.4.13) |
а ограничивающие идеальные токонесущие поверхности не влияют на скорость распространения в линии [14.5]. В частности, в воздушной линии ( 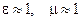 ), как и следовало ожидать, ), как и следовало ожидать,  . .
|
Из (14.3.4) следует, что комплексные амплитуды напряжения и тока в падающей волне отличаются лишь коэффициентами  . Найдем связь между ними, подставив оба равенства (14.3.4) в одно из телеграфных уравнений (14.2.3), например, в первое, и учитывая (14.2.7), тогда получим
. Найдем связь между ними, подставив оба равенства (14.3.4) в одно из телеграфных уравнений (14.2.3), например, в первое, и учитывая (14.2.7), тогда получим
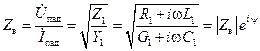 , Ом. , Ом.
| (14.4.14) |
Поскольку 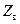 есть отношение комплексных амплитуд напряжения и тока в падающей волне, оно называется волновым сопротивлением эквивалентной ЛП. Это один из важнейших вторичных параметров ЛП. Как видно из (14.4.14), в общем случае волновое сопротивление – комплекснозначная функция
есть отношение комплексных амплитуд напряжения и тока в падающей волне, оно называется волновым сопротивлением эквивалентной ЛП. Это один из важнейших вторичных параметров ЛП. Как видно из (14.4.14), в общем случае волновое сопротивление – комплекснозначная функция 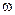 . Однако, в идеализированном случае отсутствия потерь (
. Однако, в идеализированном случае отсутствия потерь (  )
) 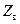 действительно, не зависит от
действительно, не зависит от 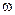 и равно
и равно
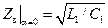 . .
| (14.4.15) |
Аналогичным образом находим:
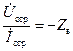 . .
| (14.4.16) |
Различие в знаках между (14.4.14) и (14.4.16) связано с тем, ток отраженной волны направлен противоположно току падающей волны.
Из (14.4.14) легко выразить модуль 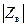 и аргумент
и аргумент 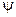 волнового сопротивления:
волнового сопротивления:
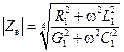 , ,
| (14.4.17) |
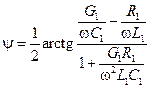
| (14.4.18) |
Как и следовало ожидать, в идеализированном случае отсутствия потерь (  ) (14.4.17) переходит в (14.4.15), а
) (14.4.17) переходит в (14.4.15), а  , т. е. напряжение и ток синфазны.
, т. е. напряжение и ток синфазны.
Частные решения волнового уравнения
Решение граничной задачи
Вернемся к общим решениям (14.3.1). Для нахождения частных решений необходимо задавать граничные условия и определять коэффициенты  . Как отмечено выше, решения для напряжения и тока в (14.3.1) не являются независимыми; действительно, подставив в (14.4.14) и (14.4.16)
. Как отмечено выше, решения для напряжения и тока в (14.3.1) не являются независимыми; действительно, подставив в (14.4.14) и (14.4.16) 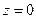 , получаем
, получаем
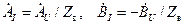 , ,
| (14.5.1) |
и решения (14.3.1) можно переписать в виде
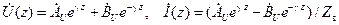 . .
| (14.5.2) |
Таким образом, для получения частного решения необходимо определить только два коэффициента 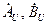 . Удобно и физично в качестве граничных условий взять напряжение и ток на нагрузке (
. Удобно и физично в качестве граничных условий взять напряжение и ток на нагрузке ( 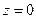 ):
):
 . .
| (14.5.3) |
Тогда из (14.5.2) при 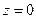 найдем:
найдем:
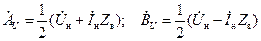 . .
| (14.5.4) |
Подставив (14.5.4) в (14.5.2) и учитывая равенства
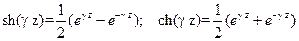 , ,
| (14.5.5) |
получим:
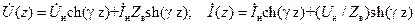 . .
| (14.5.6) |
Если в (14.3.4) и (14.3.5) положить 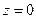 , то окажется, что комплексные коэффициенты суть комплексные амплитуды падающих и отраженных волн напряжения и тока на нагрузке:
, то окажется, что комплексные коэффициенты суть комплексные амплитуды падающих и отраженных волн напряжения и тока на нагрузке:
 . .
| (14.5.7) |
Если эти комплексные амплитуды считать заданными, то равенства (14.3.1) также можно считать частными решениями волновых уравнений (14.2.6). Разница между частными решениями (14.3.1) и частными решениями (14.5.6) состоит в том, что первые выражены через комплексные амплитуды падающих и отраженных волн на нагрузке, а вторые – через комплексные амплитуды полных напряжения и тока на нагрузке.
В идеализированном случае отсутствия потерь (  )
) 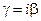 и с учетом равенств
и с учетом равенств
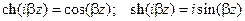
| (14.5.8) |
решения (14.5.6) можно записать в виде
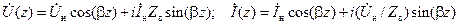 . .
| (14.5.9) |
Это же выражение можно получить и из (14.3.1), используя (14.3.2) и (14.5.1). С другой стороны, учтя (14.5.7), можно в случае отсутствия потерь записать (14.3.1) в виде:
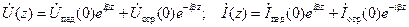 . .
| (14.5.10) |
Коэффициент отражения и входное сопротивление
Обозначим отношение комплексных амплитуд напряжений падающей и отраженной волн на нагрузке:
 . .
| (14.6.1) |
Комплексная величина 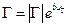 называется коэффициентом отражения по напряжению, является важным параметром системы «ЛП+нагрузка» и, как показано ниже, зависит от соотношения нагрузки
называется коэффициентом отражения по напряжению, является важным параметром системы «ЛП+нагрузка» и, как показано ниже, зависит от соотношения нагрузки 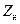 и волнового сопротивления ЛП
и волнового сопротивления ЛП 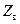 .Аналогичное отношение токов, которое можно назвать коэффициентом отражения по току, в силу (14.5.1), равно:
.Аналогичное отношение токов, которое можно назвать коэффициентом отражения по току, в силу (14.5.1), равно:
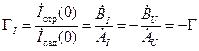 , ,
| (14.6.2) |
и на практике не применяется, поэтому слова «по напряжению» в названии 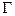 можно отбросить.
можно отбросить.
Теперь решения (14.5.10) можно переписать в виде:
 . .
| (14.6.3) |
Другим важным параметром системы «ЛП+нагрузка» является входное сопротивление нагруженной линии
 , ,
| (14.6.4) |
связанное с трансформирующими свойствами отрезка линии.
ЛП с малыми потерями
Как показано выше, такие вторичные параметры ЛП, как коэффициент ослабления 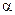 , коэффициент фазы
, коэффициент фазы  , фазовая скорость
, фазовая скорость 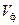 , длина волны в линии
, длина волны в линии  , волновое сопротивление
, волновое сопротивление 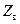 , и такие функции, как
, и такие функции, как 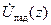 ,
, 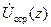 и др., выражаются через первичные параметры
и др., выражаются через первичные параметры 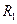 ,
, 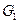 ,
, 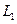 ,
,  . В общем случае произвольных первичных параметров эти выражения сложны и громоздки (см. (14.4.4), (14.4.5)), что мешает практическому использованию теории эквивалентных ЛП. С другой стороны, в предположении отсутствия потерь (и в металле, и в диэлектрике) эти соотношения резко упрощаются, но само это предположение является теоретической идеализацией, и использование получаемых простых соотношений создает ошибки, исследование величин которых представляет собой непростую задачу.
. В общем случае произвольных первичных параметров эти выражения сложны и громоздки (см. (14.4.4), (14.4.5)), что мешает практическому использованию теории эквивалентных ЛП. С другой стороны, в предположении отсутствия потерь (и в металле, и в диэлектрике) эти соотношения резко упрощаются, но само это предположение является теоретической идеализацией, и использование получаемых простых соотношений создает ошибки, исследование величин которых представляет собой непростую задачу.
Оказывается, однако, что современные ЛП часто, если не сказать всегда, принадлежат к классу линий с малыми потерями, для которых приближенные соотношения вторичных и первичных параметров компромиссны по сложности, а оценки ошибок очевидны. Примем в качестве критерия малости потерь линии условия [14.6]:
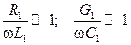 . .
| (14.7.1) |
Представив постоянную распространения  в виде:
в виде:
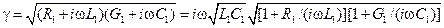 , ,
| (14.7.2) |
разложим ее по степеням отношений 
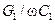 , удерживая члены второго порядка этих отношений, тогда получим:
, удерживая члены второго порядка этих отношений, тогда получим:
 ; ;
| (14.7.3) | |
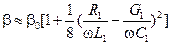 , ,
| (14.7.4) | |
где 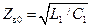 – волновое сопротивление линии без потерь (см. (14.4.15)),
– волновое сопротивление линии без потерь (см. (14.4.15)),
 – коэффициент фазы линии без потерь (см. (14.4.6)).
– коэффициент фазы линии без потерь (см. (14.4.6)).
Относительная ошибка при использовании этих формул определяется модулем первого отброшенного члена в разложении.
В современных ЛП потери в диэлектрике пренебрежимо малы по сравнению с потерями в металле, это означает, что члены с 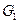 в обеих формулах пренебрежимы, и формулы упрощаются:
в обеих формулах пренебрежимы, и формулы упрощаются:
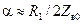 ; ;
| (14.7.5) | |
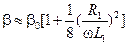 . .
| (14.7.6) | |
Для конкретной ЛП, т. е. при заданных первичных параметрах, условия (14.7.1) выполняются тем лучше, чем больше частота; начиная с некоторой частоты и для более высоких частот становится приемлемым нулевое приближение в используемом разложении ( 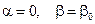 ), т. е. предположение об отсутствии потерь.
), т. е. предположение об отсутствии потерь.
Связь коэффициента отражения с нагрузкой
Пусть эквивалентная ЛП нагружена на, в общем случае – комплексное, сопротивление 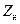 (рис. 12.1.1). Комбинируя (14.3.2), (14.4.14), (14.4.16), (14.5.1) и очевидное равенство
(рис. 12.1.1). Комбинируя (14.3.2), (14.4.14), (14.4.16), (14.5.1) и очевидное равенство
 , ,
| (14.8.1) |
получим [14.5]:
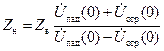 . .
| (14.8.2) |
Поделив числитель и знаменатель на  и учтя определение (14.6.1) коэффициента отражения
и учтя определение (14.6.1) коэффициента отражения 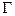 , найдем:
, найдем:
 , ,
| (14.8.3) |
откуда
 , ,
| (14.8.4) |
т. е. коэффициент отражения 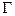 полностью определяется (комплексным) отношением
полностью определяется (комплексным) отношением 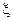 сопротивления нагрузки и волнового сопротивления.
сопротивления нагрузки и волнового сопротивления.
В большинстве случаев при конструировании радиотехнических устройств СВЧ –диапазона требуется добиваться, насколько возможно, согласования ЛП и нагрузки. Так, «…со знанием параметров рассеяния транзистора конструирование усилительных, осцилляторных и смесительных цепей сводится к задаче импедансного согласования» [14.3]. В измерительных приборах СВЧ-диапазона проблема согласования стоит особенно остро, т. к. именно рассогласованиям обязан ряд ошибок измерения. Из формулы (14.8.4) видно, что единственный способ избежать отражения от нагрузки, т. е. добиться равенства 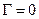 , – это выбрать сопротивление нагрузки равным волновому сопротивлению линии:
, – это выбрать сопротивление нагрузки равным волновому сопротивлению линии: 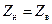 . Если волновое сопротивление ЛП чисто активно:
. Если волновое сопротивление ЛП чисто активно: 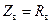 , то согласующее сопротивление должно быть также активным и равным волновому:
, то согласующее сопротивление должно быть также активным и равным волновому: 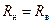 .
.
Подставляя в (14.8.4) выражения  ;
; 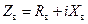 , получим:
, получим:
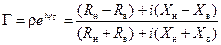 . .
| (14.8.5) |
На практике ЛП рассчитываются и изготавливаются так, чтобы волновое сопротивление было чисто активным, т. е.  =0. Учитывая это, перепишем предыдущее выражение:
=0. Учитывая это, перепишем предыдущее выражение:
 . .
| (14.8.6) |
Отсюда найдем модуль коэффициента отражения:
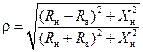 . .
| (14.8.7) |
Поскольку  и
и 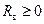 (вследствие пассивности нагрузки и ЛП), знаменатель подкоренного выражения не больше числителя, т. е.
(вследствие пассивности нагрузки и ЛП), знаменатель подкоренного выражения не больше числителя, т. е.
 . .
| (14.8.8) |
Это условие эквивалентно (14.3.3) и означает, что амплитуда отраженной волны не превосходит амплитуду падающей волны.
Распределение амплитуд напряжения и тока вдоль нагруженной линии
Интерференция волн
Из вышеизложенного следует, что в ЛП, нагруженной на сопротивление 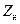 и возбуждаемой монохроматическим сигналом частоты
и возбуждаемой монохроматическим сигналом частоты 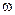 , существует две волны – падающая и отраженная, распространяющиеся в противоположные стороны. В каждой точке (сечении) линии каждая из этих волн имеет свою амплитуду и свою фазу, и происходит интерференция этих волн. Рассмотрим результаты интерференции в идеализированном случае отсутствия потерь.
, существует две волны – падающая и отраженная, распространяющиеся в противоположные стороны. В каждой точке (сечении) линии каждая из этих волн имеет свою амплитуду и свою фазу, и происходит интерференция этих волн. Рассмотрим результаты интерференции в идеализированном случае отсутствия потерь.
Относительные распределения амплитуд, их свойства
Формулы (14.6.3) дают распределения комплексных амплитуд полных напряжения и тока вдоль линии, коэффициент отражения имеет вид (см. (14.8.5)) 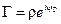 , при действительном волновом сопротивлении (
, при действительном волновом сопротивлении ( 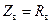 )
) 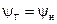 , где
, где 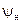 – аргумент комплексного сопротивления нагрузки:
– аргумент комплексного сопротивления нагрузки: 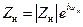 . Находя из (14.6.3) модули (амплитуды) полных напряжения и тока и деля их на те же модули в точке
. Находя из (14.6.3) модули (амплитуды) полных напряжения и тока и деля их на те же модули в точке 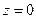 соответственно, находим относительные распределения амплитуд напряжения и тока вдоль линии:
соответственно, находим относительные распределения амплитуд напряжения и тока вдоль линии:
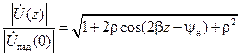 ; ;
| (14.9.1) | |
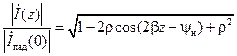 . .
| (14.9.2) | |
Непосредственно из (14.9.1), (14.9.2) следует:
1) Амплитуды напряжения и тока в линии – периодические функции продольной координаты 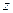 . Период
. Период 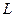 удовлетворяет условию
удовлетворяет условию 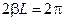 , а поскольку в случае отсутствия потерь (см. (14.4.8))
, а поскольку в случае отсутствия потерь (см. (14.4.8)) 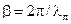 , то
, то 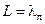 .
.
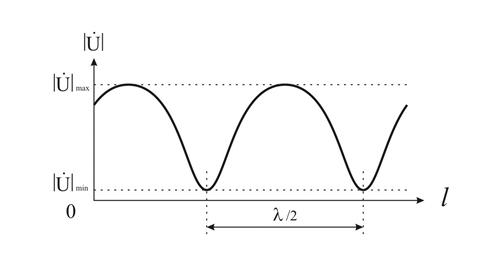
2) Относительные амплитуды напряжений и токов колеблются между  (максимум) и
(максимум) и  (минимум). Максимум относительной амплитуды напряжения достигается при
(минимум). Максимум относительной амплитуды напряжения достигается при 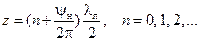 ; минимум – при
; минимум – при 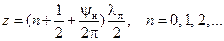 ; максимум тока находится в точке минимума напряжения, и наоборот.
; максимум тока находится в точке минимума напряжения, и наоборот.
Дата добавления: 2016-02-20; просмотров: 997;

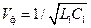 .
.