Пучности и узлы в ЛП в режиме смешанных волн

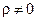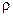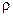3) При интерференция падающей и отраженной волн образует стоячую волну, в которой максимумы называют пучностями, а минимумы – узлами (рис. 14.9.1). Степень глубины стоячей волны определяется лишь величиной : при =1 глубина максимальна, в пучности относительная амплитуда равна 2, в узле – равна 0 (такую картину иногда называют чисто стоячей волной); при 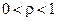пучность ниже двух, а узел выше нуля; при 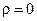стоячей волны нет: отраженная волна отсутствует, относительные амплитуды напряжения и тока при всех 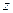равны 1, имеет место режим бегущей волны.

4) Фазовый угол 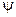влияет лишь на координаты узлов и пучностей, но не на значения амплитуды в них.

5) Как видно из рис. 14.9.1, минимум амплитуды вблизи узла выражен более резко, чем максимум амплитуды вблизи пучности. Это свойство стоячей волны важно в измерениях с помощью длинных линий: измерение положения пучности менее чувствительно, чем положения узла, зато проводится при большем «отношении сигнал-шум».

6) Для исчерпывающего описания распределения амплитуд вдоль линии достаточно изучить поведение напряжения по (14.9.1), поскольку распределение тока (14.9.2) повторяет распределение напряжения , но со смещением вдоль линии на .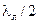

7) Для количественного описания глубины стоячей волны вводят коэффициент стоячей волны, равный отношению максимальной и минимальной амплитуд:

,

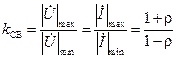(14.9.3)

откуда

.

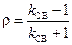(14.9.4)

Коэффициент стоячей волны – скалярная величина, принимающая значения в диапазоне

.

(14.9.5)

Левая граница этого диапазона соответствует полному согласованию, 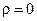, т. е. режиму бегущей волны, правая – полному рассогласованию, 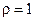, т. е. режиму чисто стоячей волны. И тот, и другой режимы на практике не достижимы в полной мере и являются математической абстракцией, приближение к которой возможно в той или иной степени. Идеально согласованная нагрузка 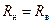невозможна из-за тепловых потерь, различных нерегулярностей и неоднородностей, обусловленных конечной точностью изготовления линии, наличием элементов крепления, несовершенством разъемов и других факторов, вызывающих появление отраженной волны. Идеальная полностью отражающая нагрузка невозможна из-за паразитных емкости, индуктивности и утечек.

Режимы работы ЛП без потерь

Обычно режимы в нагруженной ЛП разделяют на три класса:

1) Режим бегущей волны: линия согласована, 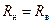, , 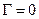отраженная волна отсутствует, распространяется только падающая волна, которая полностью поглощается нагрузкой, амплитуды напряжения и тока постоянны вдоль линии.

2) Режим чисто стоячей волны: 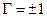, в сечении 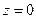амплитуда отраженной волны равна амплитуде падающей волны, энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор, , .

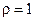3) Режим смешанных волн: 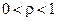, , 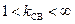часть энергии падающей волны поглощается нагрузкой, остальная ее часть в виде отраженной волны возвращается обратно в генератор, стоячая волна имеет неполную глубину, т. е. в пучности относительная глубина меньше двух, в узле относительная глубина больше нуля.

Канонические нагрузки

Рассмотрим распределения вдоль линии без потерь амплитуд напряжения и тока и входного сопротивления для нагрузок: согласованной резистивной нагрузки, холостого хода, короткого замыкания, емкости, индуктивности [14.6]. Эти нагрузки можно назвать каноническими; примеры, связанные с ними, помогают лучше понять структуру волн в нагруженной линии, а также имеют самостоятельный интерес.

Согласованная нагрузка

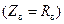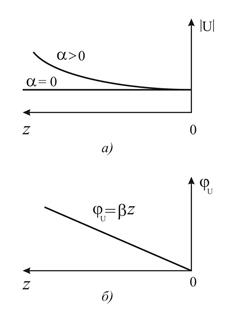
Далее считаем волновое сопротивление чисто активным , тогда согласованная нагрузка – сопротивление, равное волновому ( 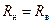). Как указано выше, при такой нагрузке получается режим бегущей волны с постоянными вдоль линии амплитудами напряжения и тока и линейной фазой (рис. 14.11.1). Напряжение и ток в этом режиме (см. (14.5.10)) равны:

,

(14.11.1)

поэтому

.

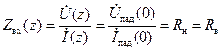(14.11.2)

Таким образом, в режиме бегущей волны входное сопротивление любого отрезка нагруженной линии независимо от его длины в точности равно волновому сопротивлению линии.