Стандартное значение волнового сопротивления

Возвращаясь к выбору отношения 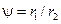и волнового сопротивления 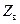коаксиала, замечаем, что этот выбор неоднозначен и зависит от критерия оптимальности.

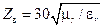1) Как показано в 13.8.4, оптимальное с точки зрения пробоя =1.648, при этом , Ом (см. (13.8.14), (13.8.15).

2) Оптимальное , при котором ослабление за счет металлических проводников минимально, есть =3.6, при этом .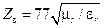

3) Так как 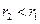, то наибольшие потери энергии происходят в центральном проводнике, поэтому увеличение его радиуса приводит к уменьшению тока проводимости и уменьшению потерь. Если увеличение 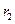сопроводить таким же увеличением 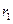(пропорциональное увеличение радиусов), то вследствие условия одноволновой передачи (13.8.10) снизится максимальная частота доступного рабочего диапазона частот; если же 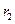увеличивать при неизменном 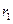, то снизится волновое сопротивление 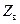, что при данной передаваемой мощности 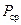приведет к увеличению тока в линии и соответствующему увеличению потерь. Оптимальное в этом смысле указано в п. 2.

4) Иногда ставят задачу задать такое , при котором минимальна разность потенциалов 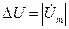между внутренним и внешним проводниками коаксиала. Оптимальное в этом смысле 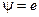=2.716, при этом .

Принятый по рекомендации Международной электротехнической комиссии международный стандарт задает для коаксиала, предназначенного для передачи «значительной» мощности, , 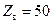Ом и сетку пар радиусов с указанным . В случае «малой» передаваемой мощности применяются коаксиалы с 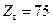Ом, а также, иногда, с Ом и 150 Ом.

Полосковые ЛП (классификация полосковых ЛП, частотные ограничения, эффективная диэлектрическая проницаемость, волновое сопротивление и погонная емкость, длина волны в линии, коэффициент фазы, затухание в линии)

Модель эквивалентной ЛП

Двухпроводная симметричная модель

Радиосистемы, работающие в диапазоне СВЧ, обычно можно представить в виде устройств СВЧ, соединенных отрезками линий передачи (ЛП) и образующих тракты СВЧ. Компоненты трактов СВЧ не являются локальными радиотехническими элементами, такими как емкость, индуктивность, резистор и их комбинации, например, резонансный контур и т. п., по той причине, что в диапазоне СВЧ характерные размеры 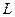устройств и ЛП не отвечают условию 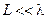. Строгое рассмотрение распространения электромагнитных сигналов в трактах СВЧ на основе краевых задач электродинамики очень сложно и выполнимо только для простейших устройств и ЛП, например, отдельных отрезков ЛП. С другой стороны, если даже такое описание распространения сигналов может быть получено, оно часто оказывается излишне подробным [14.1]. Более простой альтернативой является переход к эквивалентным схемам устройств.

Для устройств СВЧ вообще (включая отрезки ЛП) этот переход происходит по двум направлениям:

1) Проделав предварительно, насколько это возможно, декомпозицию сложной цепи на ряд более простых элементов, которые можно анализировать независимо, пытаются для каждого элемента подобрать такую схему из сосредоточенных постоянных , трансформаторов и отрезков линий передачи, которая в смысле определенных количественных критериев дает достаточно близкие к действительности результаты своей работы. В необходимых случаях должна иметься возможность связать эквивалентные параметры и интегральные параметры ЛП с волновыми параметрами строгого электродинамического описания

2) После такой же декомпозиции каждый линейный элемент представляют в виде 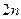-полюсника, внешние параметры которого можно описать с помощью матриц того или иного вида (см. главу 10). В необходимых случаях должна иметься возможность связать элементы описывающей матрицы (например, S-параметры) с волновыми параметрами.

Возвращаясь теперь к более узкой задаче перехода от строгого электродинамического описания (см. главу 13) ЛП к описанию на уровне более простой модели, видим, что дело сводится к построению модели эквивалентной ЛП [14.2–14.4] (мы примем именно это наименование), или эквивалентной цепи с распределенными параметрами [14.5], или длинной линии [14.6], или линии с распределенными параметрами, или эквивалентной схеме ЛП и т. п. (различные названия одного и того же понятия).

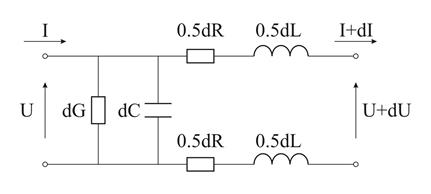
Физически модель эквивалентной ЛП можно представлять как двухпроводную линию, в которой первичными параметрами являются погонные сопротивление, проводимость, емкость и индуктивность, а вторичными – напряжение и ток. Иногда вторичные параметры называют интегральными, поскольку они выражаются интегралами от первичных параметров (точнее, они суть решения дифференциальных уравнений, в которых первичные параметры задают коэффициенты). Электромагнитные процессы в эквивалентной ЛП описываются скалярными величинами (в общем случае – комплексными) напряжения и тока как функций лишь продольной координаты. Эти функции строятся на основе векторных напряженностей электрического и магнитного поля как функций пространственных и временной координат, получаемых для каждого типа ЛП из решения соответствующей электродинамической задачи.

Прежде чем задать эквивалентную ЛП как модель конкретной физической ЛП – волноводной, коаксиальной, полосковой – следует убедиться в возможной адекватности такого перехода, в частности, в возможности связать первичные параметры эквивалентной ЛП с волновыми параметрами строгого электродинамического описания, а также определить область использования этой упрощенной модели в пространстве характеристик ЛП как устройства СВЧ. Отметим очевидные ограничения области действия модели эквивалентной ЛП [14.2]:

1) Модель можно использовать лишь в условиях (например, в частотном диапазоне) одноволнового режима. К счастью, от этого недостатка можно избавиться, отнеся отдельную эквивалентную линию каждой моде поля при многоволновой передаче.

2) Модель не пригодна для определения предельной пропускаемой мощности .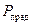

3) Модель не пригодна для анализа степени взаимной связи между открытыми ЛП.

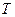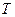Вернемся к вопросу об адекватности модели. Если основной волной физической ЛП является -волна (как в двухпроводной и коаксиальной линиях) и обеспечено условие одноволновой передачи, вопрос становится простым: поле в поперечнике линии потенциально, поэтому можно по распределению векторов электрического поля и магнитного поля -волны в поперечнике однозначно, путем контурного интегрирования, определить напряжение 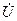и ток 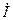как функции продольной координаты 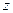. В линии без потерь эти зависимости следуют из (13.2.3) и имеют вид:

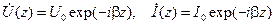
(14.1.1)

Зная функции (14.1.1), можно вычислить волновое сопротивление 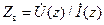и среднюю за период переносимую мощность

.

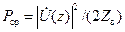(14.1.2)

Таким образом, в этом случае напряжение и ток в линии физически реальны и переход к модели эквивалентной линии адекватен.

Если основной волной физической ЛП является квазиТ-волна (как в полосковой линии) и обеспечено условие одноволновой передачи, то изложенное выше остается в силе, но уже приближенно (вопрос об ошибке модели в данном случае здесь не рассматривается).

Если в ЛП 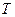-волна не распространяется (как в металлическом волноводе), то в этой ЛП нет физически реальных напряжения и тока, переносящих мощность [14.4]. В такой линии распространяются 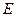-, - 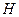или смешанные волны, и можно попытаться определить напряжение 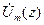и ток 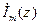эквивалентной линии формально через контурные интегралы от поперечных составляющих поля 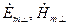. Однако, в этом случае поле, описываемое этими составляющими, не является потенциальным и функци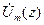и и 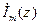определяются неоднозначно: они зависят от выбора контуров интегрирования. Эту трудность можно обойти, заранее оговорив форму контуров.

Рассмотрим этот прием на примере [14.2]. Пусть имеется прямоугольный волновод с размерами стенок 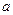(широкая) и (узкая). Как показано в главе 13, основная волна в этом случае – волна 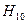. Используя выражение (13.7.4) для составляющей волны 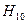, находим комплексную амплитуду напряжения между точками, лежащими на средних линиях широких стенок при :

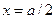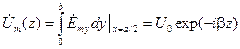
(14.1.3)

где

,

(14.1.4)

и принимаем ее за величину, пропорциональную комплексной амплитуде напряжения в эквивалентной линии:

.

(14.1.5)

Как отмечено в 13.7, 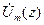определено с точностью до 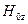, такова же степень неопределенности формулы (14.1.5): с точностью до .

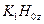Используя выражение (13.7.4) для составляющей 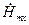волны 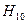, находим комплексную амплитуду тока, текущего по нижней ( 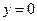) широкой стенке волновода:

,

(14.1.6)

где

,

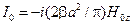(14.1.7)

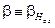, и принимаем ее за величину, пропорциональную комплексной амплитуде 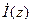тока в эквивалентной линии:

.

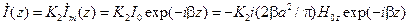(14.1.8)

Как отмечено в 13.7, 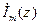определено с точностью до 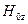, такова же степень неопределенности формулы (14.1.8): с точностью до .

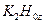Учитывая (14.1.3) и (14.1.6), можно определить волновое сопротивление для волны :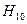

,

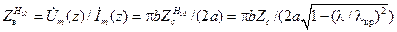(14.1.9)

и принять его за волновое сопротивление для эквивалентной линии. Поскольку (14.1.5) определено с точностью до коэффициента 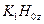, а (14.1.8) – с точностью до коэффициента 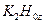, то (14.1.9) определено с точностью до коэффициента

.

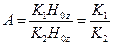(14.1.10)

Это значит, что, изменив форму контура интегрирования или даже саму методику определения напряжения 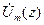и тока 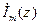в ЛП, мы получим другое выражение для 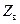, но во всех случаях формула для 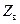будет иметь вид:

,

(14.1.11)

где 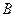– коэффициент, зависящий только от способа вычисления 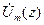и 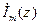. Неопределенность в выборе этого коэффициента существенного значения не имеет [14.2], т. к. при проектировании цепей СВЧ важно знать отношение волновых сопротивлений соединяемых отрезков ЛП, а не конкретные значения каждого из них.

Таким образом, любую из рассмотренных в главе 13 линий передачи (волноводную, коаксиальную, полосковую) в интересах анализа можно заменить эквивалентной ЛП, в которой распространяются соответствующие волны напряжения и тока. И хотя обоснование правомерности этой замены для разных типов ЛП имеет разную степень убедительности, модель эквивалентной ЛП чрезвычайно полезна при инженерном проектировании трактов СВЧ, оптимальна по сложности и информативности описания и многократно проверена экспериментально.

Для анализа процессов, происходящих в анализаторе цепей, концепция эквивалентных ЛП имеет особое значение: анализатор нацелен на измерение характеристик тестируемого устройства на уровне подробности 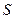-параметров (ВАЦ измеряет комплексные значения 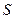-параметров, САЦ – модули 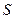-параметров), этому уровню подробности точно соответствует описание ЛП в модели эквивалентных линий.