Дифракция Френеля на круглом отверстии

ДИФРАКЦИЯ

Принцип Гюйгенса- Френеля. Зоны Френеля.

Дифракция – огибание волнами препятствий, отклонение распространения волн вблизи препятствий от законов геометрической оптики. Мы будем рассматривать плоские или сферические волны. Тип волны зависит от формы волновой поверхности – поверхности постоянной фазы. Когда фаза является постоянной на плоскости, имеем плоскую волну. Когда поверхность постоянной фазы есть сфера, получаем сферическую волну. Объяснение дифракции основано на использование двух принципов: принципе Гюйгенса и принципе Гюйгенса – Френеля. Принцип Гюйгенса позволяет определить волновой фронт в любой момент времени, если его форма известна в заданный момент. Он гласит: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн определяет волновой фронт в следующий момент времени. Принцип Гюйгенса позволяет определить направление распространения волны, но ничего не говорить об интенсивности волн, распространяющихся в разных направлениях. Для решения этой проблемы Френель предложил использовать интерференцию вторичных волн. Это формулируется в виде принципа Гюйгенса – Френеля: световая волна, испускаемая источником 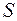, представляется как результат суперпозиции когерентных вторичных волн, излучаемых фиктивными источниками. Обычно считается, что эти источники расположены на волновой поверхности. Это приводит к тому, что вторичные волны имеют одинаковые фазы. Кроме того, Френель исключил 1) возникновение обратных вторичных волн, и 2) любое непрозрачное препятствие на пути распространения волн не является источником вторичных волн. Для нахождения интерференционной картины вторичных волн Френель предложил метод зон. Рассмотрим однородную среду, в которой распространяется сферическая волна от точечного источника 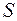. Найдем в произвольной точке 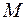амплитуду волны.

Рис

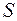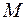Волновой фронт Ф – это сфера. Точки и соединим прямой SM. Проведем сферу, соответствующую волновому фронту. Волновую поверхность разобьем на кольцевые зоны. Они удовлетворяют условию: расстояние от краев зоны до точки М отличаются на 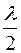. Из рисунка 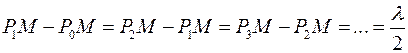. Для построения зон проводим сферы с началом в точке 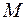, радиусом: ,

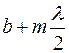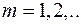
Колебания от соседних зон проходят расстояния до точки 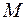, которые отличаются на 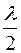. Поэтому они приходят в противофазе и ослабляются. Т.о. амплитуда в точке 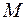равна

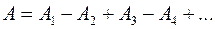(1)

где 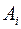- амплитуда колебаний 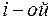зоны. Найдем .

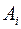Рис

Внешняя граница зоны с номером 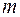выделяет на волновой поверхности сферический сегмент высоты 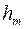. Площадь этого сегмента 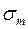. Тогда площадь зоны Френеля с номером 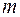равна 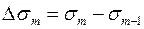. Из рисунка находим

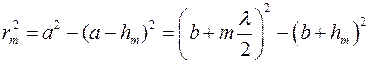
Из последнего равенства с условиям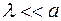и и 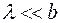, находим

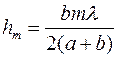(2)

Площади сегмента 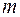и зоны Френеля с номером 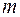равны, соответственно: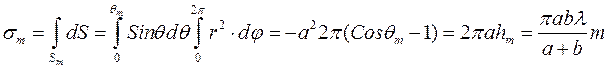

(3)

Воспользовались 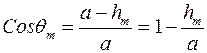и .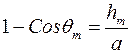

Из (3) видим, что площадь зоны Френеля, 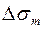, не зависит от 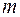. Тогда, при условии, что 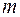не велико, площади зон Френеля одинаковы. Далее, Френель предположил, что с ростом угла 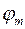действие зоны 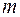в точке 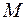уменьшается. Это эквивалентно 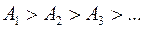. Число зон Френеля на полусфере очень велико. Поэтому принимаем следующее приближение для зоны :

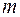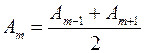(4)

Тогда, используя Ур.(1), получаем

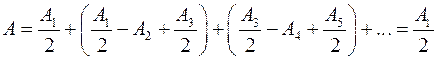(5)

Т.о. действие всей поверхности в точке 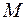равно действию малого участка, меньшего центральной зоны. Если в выражении для 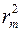положить 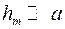(при не очень больших 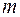), тогда 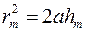. Заменяя значение 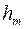, получим значение радиуса внешней границы 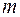-ой зоны Френеля:

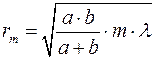(6)

Дифракция Френеля на круглом отверстии

Дифракция Френеля или дифракция в сходящихся лучах. Точка 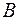- точка наблюдения дифракционной картины. Экран и плоскость отверстия параллельны.

Рис.

Разобьем волновую поверхность, которая имеет форму сферы, в отверстии на зоны Френеля. Амплитуда результирующего колебания

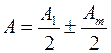
где знак « + » соответствует нечетным значениям 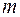, знак « - » соответствует четным значениям 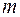. Если отверстие открывает одну зону Френеля, то . Интенсивность света, а она пропорциональна 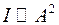, в этом случае больше в 4 раза интенсивности без отверстия. Если отверстие открывает две зоны Френеля, то их действие в точке 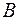практически взаимно сокращаются из-за интерференции. Т.о. интерференционная картина будет состоять из чередующихся темных и светлых колец с центром в точке 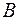. Интенсивность светлых колец будет уменьшаться с увеличением расстояния от центра картины.