Дифракция Фраунгофера на одной щели
Или дифракция в параллельных лучах. Рассмотрим дифракцию от бесконечно длинной щели. Плоская монохроматическая световая волна падает нормально плоскости щели шириной 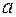 .
.
Рис
Оптическая разность хода между крайними лучами 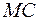 и
и 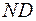 равна
равна
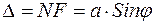 (1)
(1)
В точках 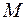 и
и 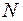 фазы лучей совпадают. Используем принцип Гюйгенса – Френеля. Разобьем открытую часть волновой поверхности на зоны Френеля, которые имеют вид полос, параллельных ребру
фазы лучей совпадают. Используем принцип Гюйгенса – Френеля. Разобьем открытую часть волновой поверхности на зоны Френеля, которые имеют вид полос, параллельных ребру 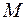 . Ширина каждой зоны выбирается таким образом, чтобы разность хода от краев этих зон была равной
. Ширина каждой зоны выбирается таким образом, чтобы разность хода от краев этих зон была равной 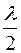 . На ширине щели уместиться
. На ширине щели уместиться 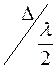 зон. Число зон зависит от угла
зон. Число зон зависит от угла 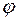 . Амплитуды вторичных волн в плоскости щели равны, т.к. площади зон Френеля равны. Применяя рассуждения, аналогичные выше изложенным, находим для четного числа зон Френеля:
. Амплитуды вторичных волн в плоскости щели равны, т.к. площади зон Френеля равны. Применяя рассуждения, аналогичные выше изложенным, находим для четного числа зон Френеля:
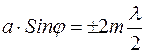 ,
, 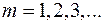 (2)
(2)
в точке 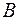 наблюдается дифракционный минимум. Для нечетного числа зон Френеля имеем
наблюдается дифракционный минимум. Для нечетного числа зон Френеля имеем
 ,
, 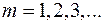 (3)
(3)
наблюдается дифракционный максимум, соответствующий одной некомпенсированной зоне Френеля. В точке 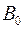 наблюдается центральный дифракционный максимум с наибольшей интенсивностью. Это результат действия одной зоны Френеля. Итоговый спектр имеет вид.
наблюдается центральный дифракционный максимум с наибольшей интенсивностью. Это результат действия одной зоны Френеля. Итоговый спектр имеет вид.
Рис.
С ростом ширины щели ( 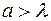 ) дифракционные полосы становятся уже и ярче, а число полос растет. Для
) дифракционные полосы становятся уже и ярче, а число полос растет. Для 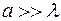 остается изображение источника.
остается изображение источника.
Дата добавления: 2016-02-20; просмотров: 510;
