Дифракция Френеля на круглом отверстии и диске.

Этот тип дифракции реализуется в сходящихся лучах (в сферических волнах) при условии, что размеры отверстия (или препятствия) r_i сравнимы с произведением расстояния до экрана l на длину волны λ:

.

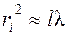Рассмотрим вначале дифракцию на круглом отверстии. Допустим, световая волна распространяется от точечного источника S (см. рис. 3.3) и встречает на своем пути отверстие радиуса r_i. При этом на экране, находящемся на расстоянии l

от отверстия, вокруг точки P возникает дифракционная картина. Разобьем открытую часть волновой поверхности на зоны Френеля.

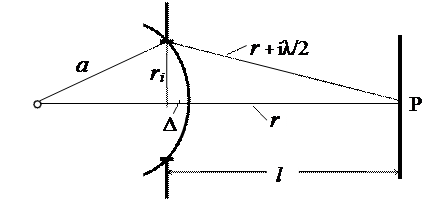
Рис. 3.3

Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке P всеми зонами, на основании рассмотренного в предыдущем параграфе будет:

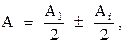
где знак плюс соответствует нечетным i и минус – четным.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Когда отверстие открывает нечетное число зон Френеля, то интенсивность в точке P будет больше, чем при свободном распространении волны; если четное число зон Френеля, то интенсивность будет равна нулю. Таким образом, дифракционная картина от круглого отверстия вблизи точки P будет иметь вид чередующихся темных и светлых колец с центрами в точке P. При этом если i четное, то в центре будет темное кольцо, а если i нечетное – то светлое кольцо.

От числа i зависит и радиус отверстия, дающего максимум или минимум в центре дифракционной картины. Из рисунка (см. выше) следует, что на основании теоремы Пифагора можно записать:

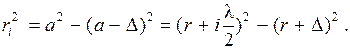
Отсюда при Δ << a и λ << r имеем:

.

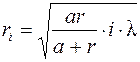Следовательно, при различных значениях i радиус отверстия, дающий в центре темное или светлое пятно, будет различен при остальных постоянных параметрах установки (a и r).

В случае дифракции на диске результирующая амплитуда в центре экрана будет определяться (как было рассмотрено в предыдущем параграфе):

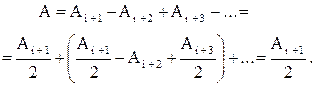
Следовательно, в центре дифракционной картины всегда будет наблюдаться максимум(так называемое, пятно Пуассона - см. рис. 3.4). А следом за тенью от диска будут располагаться дифракционные кольца, интенсивность которых будет постепенно уменьшаться.