Под углом друг к другу
Задача 15.3. Две одинаковые собирающие линзы 1 и 2, имеющие каждая фокусное расстояние F, расположены так, что их главные оптические оси составляют угол a,и главная оптическая ось первой линзы проходит через центр второй линзы (рис. 15.12). На главной оптической оси первой линзы на расстоянии F расположен точечный источник света S. Найти расстояние между источником света и его изображением в паре линз. Расстояние между центрами линз равно l.
| F l a | 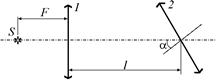 Рис. 15.12 Рис. 15.12
|
| х = ? | |
Решение. Построим изображение источника. Проведем произвольный луч SA из точки S к линзе 1 (рис. 15.13). Поскольку источник S находится в главном фокусе этой линзы, то после преломления луч SA пойдет параллельно главной оптической оси линзы 1 до пересечения с линзой 2 в точке В.
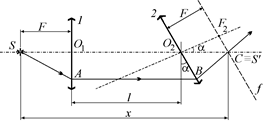 Рис. 15.13
Рис. 15.13
Луч О1О2, проходящий через оптические центры обеих линз, проходит через систему, не преломляясь. Обозначим главный фокус F2 линзы 2 и проведем фокальную плоскость f линзы 2. Тогда параллельные лучи АВ и О1О2 после преломления в линзе 2 пересекутся в побочном фокусе – точке С. Эта точка С и будет изображением S¢ точки S в системе двух линз, т.е. C º S¢.
Искомая величина х, как видно их рис. 15.13, равна
х = SO1 + O1O2 + O2С,
где SO1 = F, O1O2 = l, а отрезок О2С легко определить из DО2F2С: 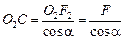 . Тогда
. Тогда 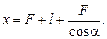
Ответ: 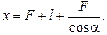
СТОП! Решите самостоятельно: С7, D1, D2.
Дата добавления: 2016-04-11; просмотров: 2593;
