Задачи очень трудные. D1. Две одинаковые собирающие линзы 1 и 2, имеющие каждая фокусное расстояние F, расположены так, что их главные оптические оси образуют угол a и главная

D1. Две одинаковые собирающие линзы 1 и 2, имеющие каждая фокусное расстояние F, расположены так, что их главные оптические оси образуют угол a и главная оптическая ось второй линзы проходит через центр первой (рис. 15.28). В фокусе первой линзы расположен точечный источник света S. Найти расстояние между источником света и его изображением в системе двух линз.

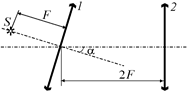
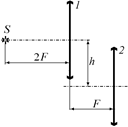
Рис. 15.28 Рис. 15.29

D2. Две собирающие линзы с одинаковыми фокусными расстояниями F расположены на расстоянии F друг от друга (рис. 15.29). Оптическая ось первой линзы парал­лельна оптической оси второй линзы и находится на рас­стоянии h от нее. Найти расстояние между точечным источником света S, расположенным на расстоянии 2F от первой линзы на ее главной оптической оси, и его изображени­ем в паре линз.

D3.Система состоит из двух линз (собирающей и рассеивающей) с
одинаковыми по модулю фокусными расстояниями. Главные оптические оси линз совпадают. С помощью этой системы на экране получено изображение Солнца. Когда линзы поменяли местами, экран пришлось передвинуть на s = 30 см. Каково фокусное расстояние F собирающей линзы?

D4.Объектив фотоаппарата состоит из двух линз. Рассеивающая линза с фокусным расстоянием F₁= –50 мм расположена на расстоянии
l = 45 см от пленки. Где должна находиться собирающая линза с фокусным расстоянием F₂= 80 мм, чтобы на пленке получались резкие изображения удаленных предметов?

Микроскоп

Назначение у микроскопа такое же, как и у лупы: «увеличивать» мелкие предметы (иногда даже не видимые невооруженным глазом) настолько, чтобы их можно было хорошо рассмотреть.

Вспомним принцип действия лупы. Лупа, как мы уже знаем, – это короткофокусная собирающая линза. Она дает мнимое увеличенное изображение предмета, который помещается за фокальной плоскостью лупы рядом с фокусом (рис. 16.1). При этом угол зрения, под которым глаз, располагающийся за лупой, наблюдает это изображение, равен

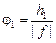. (1)

Рис. 16.1

Из подобия DОАВ и DОА¢В¢ следует

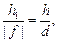(2)

отсюда

(3)

Поскольку изображение мнимое, то f < 0. Формула линзы имеет вид:

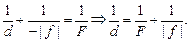(4)

Подставим значение 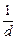из формулы (4) в формулу (3) и получим:

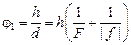. (5)

Если мы хотим, чтобы глаз не напрягался, то изображение А¢В¢ должно быть бесконечно удалено от глаза, т.е. | f | ® ¥, тогда 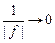, а величина j₁ будет равна

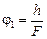. (6)

В то же время угол зрения, под которым виден тот же предмет высотой h невооруженным глазом (рис. 16.2), равен

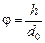, (7)

где d₀ = 25 см – расстояние наилучшего зрения. То есть лупа увеличила угол зрения с величины 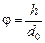до величины 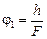(F < d₀).

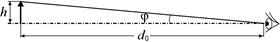Рис. 16.2

Вспомним, что величина, которая показывает, во сколько раз увеличился угол зрения за счет действия лупы, равна

k₀ = .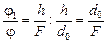

Как мы уже знаем, эта величина называется стандартным угловым увеличениемлупы. Запомним:

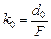. (16.1)

Заметим, что изображение А¢В¢ (см. рис. 16.1) необязательно «отправлять» на бесконечность. Можно так подобрать расстояние d от лупы до рассматриваемого предмета АВ, чтобы его изображение оказалось на расстоянии наилучшего зрения: | f | = d₀ = 25 см от глаза. Тогда угол j₁, под которым глаз будет наблюдать изображение А¢В¢, согласно формуле (5) будет равен

. (8)

Найдем угловое увеличение в этом случае:

.

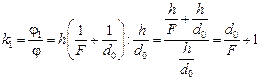Как видим, k₁ больше k₀ ровно на единицу!

Запомним формулу

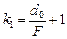. (16.2)

Величину k₁, как мы уже знаем, называют максимальным угловым увеличением лупы.

Автор: А как Вы думаете, почему с помощью лупы невозможно добиться очень большого углового увеличения? Ну, например, в 1000 раз?

Читатель: Если взять k₀ = 1000, то по формуле (16.1) получим 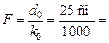0,025 см = 0,25 мм. Даже если и удастся изготовить тонкую линзу с таким фокусным расстоянием, то пользоваться ей будет практически невозможно.

Автор: Вы правы! Максимальное угловое увеличение лупы не более 40. А иногда необходимо рассматривать очень мелкие предметы, например, бактерии, размеры которых всего несколько микрометров. Здесь необходимо увеличение как раз в 1000 раз! Поэтому и понадобился более мощный оптический прибор – микроскоп.