ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. А1.Биолог, рассматривая спору гриба в микроскоп, опре­делил диаметр её изображения d = 1,2 см

Задачи легкие

А1.Биолог, рассматривая спору гриба в микроскоп, опре­делил диаметр её изображения d = 1,2 см. Каков истинный размер споры, если объектив микроскопа даёт стократное увели­чение, а окуляр – шестикратное?

А2.Диаметр красного кровяного шарика 7,5 мкм. Каков диаметр его изображения в микроскопе, если объектив микроскопа дает двухсоткратное увеличение, а окуляр – шестикратное?

А3.Микроскоп состоит из объектива и окуляра, расстояние между главными фокусами которых 18 см. Найти увеличение, даваемое микроскопом, если фокусные расстояния объектива и оку­ляра соответственно равны 2,0 и 40 мм.

Задачи средней трудности

В1. Главное фокусное расстояние объектива микро­скопа F₁ = 3,0 мм, окуляра F₂ = 5,0 см. Предмет находится от объектива на расстоянии d = = 3,10 мм. Найти увеличение микроскопа для нормального глаза. Рассмотреть случаи: 1) изображение располагается на расстоянии d₀ = 25,0 см от окуляра; 2) в глаз из окуляра идут параллельные пучки лучей.

В2.Фокусные расстояния объектива и окуляра мик­роскопа F₁= 8,0 мми F₂ = 5,0 см, расстояние между объекти­вом и окуляром l = 21 см. Найти увеличение k микроскопа.

В3. Фокусное расстояние объектива микроскопа F₁ = 0,3 см, длина тубуса микроскопа d = 15 см, увеличение микроскопа k = 2500. Найти фокусное расстояние F₂оку­ляра.

В4. Как расположить друг относительно друга две линзы с фокусными расстояниями 13 и 7,5 см, чтобы по­лучить модель микроскопа, увеличивающего в 10 раз? Сде­лайте это.

Задачи трудные

С1. Предмет находится на расстоянии d = 6,l мм от объектива микроскопа. Фокусное расстояние окуляра F₂= 1,25 см, увеличение микроскопа k = 1200. Найти фокус­ное расстояние объектива F₁если расстояние наилучшего зрения d₀ = 25 см.

C2.Фокусные расстояния объектива и окуляра микро­скопа F₁ = 4 мм и F₂ = 2,5 мм. Предмет находится на рас­стоянии а = 0,2 мм от фокуса объектива. Найти увеличение k и длину d тубуса микроскопа.

С3. Фокусное расстояние объектива микроскопа F₁ = 1,25 мм, окуляра F₂= 10,0 мм. Расстояние между объективом и окуляром l = 16,0 см. Где должен быть помещен рассматриваемый объект и каково увеличение микро­скопа для наблюдателя, расстояние наилучшего зрения которого d₀ = 25,0 см?

С4.Фокусное расстояние объектива микроскопа F₁= 3,5 мм, а увели­чение микроскопа k = 100. Определите фокусное расстояние F₂окуляра, если он расположен на расстоянии l = 12,4 см от объектива.

Телескоп

Труба Кеплера

Знаменитый немецкий астроном Иоганн Кеплер (1571–1630) в 1611 году изобрел зрительную трубу, которая позволяла наблюдать удаленные объекты. Разумеется, Кеплера как астронома больше всего интересовали небесные тела: Луна, планеты, звезды.

Своим устройством и принципом действия труба Кеплера очень напоминает микроскоп. Она состоит из двух собирающих линз (объектива и окуляра), которые располагаются вдоль общей главной оптической оси. Как и в микроскопе, изображение, создаваемое объективом, является действительным и находится в фокальной плоскости окуляра. Как и в микроскопе, окуляр действует как лупа, через которую мы разглядываем действительное перевернутое изображение, созданное объективом.

Окуляр создает прямое увеличенное мнимое изображение действительного изображения, поэтому, как и в микроскопе, мы видим предмет «вверх ногами» (рис. 17.1).

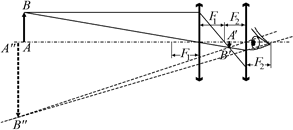
Рис. 17.1

Заметим, что поскольку это изображение действительное, то и в микроскопе, и в трубе Кеплера его можно сфотографировать, если поместить в соответствующем месте фотопластинку.

Основное отличие трубы от микроскопа состоит в том, что рассматриваемый предмет АВ очень большой и находится очень далеко. Поэтому изображение А¢В¢ – значительно меньше предмета и находится практически в фокальной плоскости объектива. Ясно, что чем больше фокусное расстояние объектива, тем больше изображение А¢В¢ (это очевидно из подобия DАОВ и DА¢ОВ¢). Поэтому в отличие от микроскопа объектив у трубы Кеплера должен быть длиннофокусным.

Что касается окуляра, то тут больших отличий от микроскопа нет: чем меньше фокусное расстояние лупы, тем большее угловое увеличение она дает. Поэтому, как и в микроскопе, окуляр должен быть короткофокусным.

Читатель: Значит, изображение в трубе Кеплера перевернутое. По-моему, это не очень удобно.

Автор: Вы правы, особенно если эта труба используется как бинокль. Но на самом деле «перевернуть» изображение еще раз – дело нехитрое. В бинокле для этого используют специальные «оборачивающие» призмы (рис. 17.2).

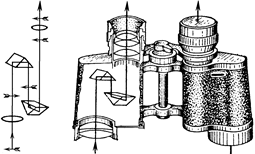
Рис. 17.2

Читатель: А как вычислить угловое увеличение трубы Кеплера?

Автор: Пусть труба Кеплера наведена «на бесконечность», т.е. настроена на наблюдение очень далеких объектов. Тогда действительное изображение объекта получится в задней фокальной плоскости объектива, т.е. на расстоянии F₁ от объектива, если F₁ – фокусное расстояние объектива.

Если мы хотим проводить наблюдение без напряжения зрения, то лучи из окуляра должны выходить параллельными пучками. А для этого действительное изображение объекта должно находиться в передней фокальной плоскости окуляра.

Таким образом, действительное изображение объекта должно одновременно находиться в задней фокальной плоскости объектива и в передней фокальной плоскости окуляра. А значит, расстояние l между окуляром и объективом (длина трубы) должно равняться сумме фокусных расстояний объектива и окуляра:

l = F₁ + F₂. (17.1)

Пусть лучи от двух удаленных точечных объектов S₁ и S₂, угловое расстояние между которыми равно a, попадают в объектив трубы Кеплера (рис. 17.3).

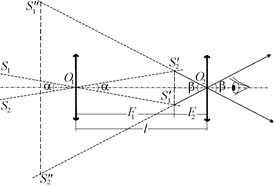Рис. 17.3

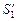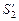Действительные изображения объектов и получатся в задней фокальной плоскости объектива, которая одновременно является передней фокальной плоскостью окуляра. При этом 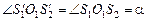(как вертикальные). Окуляр образует мнимые изображения 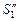и 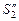действительных изображени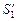й и 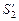. Причем эти мнимые изображения будут лежать на продолжениях лучей и 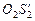. Поэтому угол зрения b, под которым мы будем видеть мнимое изображение отрезка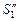 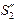равен .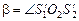

Угловое увеличение k зрительной трубы – это отношение углов зрения b и a: 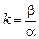. Поскольку все углы мы считаем малыми, то:

из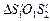

(1)

из

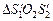
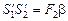. (2)

Приравнивая правые части равенств (1) и (2), получим

.

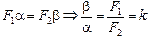Запомним: угловое увеличение трубы Кеплера равно

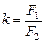. (17.2)

Читатель: Интересно, а если убрать окуляр, получится хоть какое-то угловое увеличение?

Автор: Получится! Но гораздо меньшее, чем с окуляром. В этом случае мы будем вынуждены рассматривать действительное изображение с расстояния наилучшего зрения d₀ = 25 см (иначе мы его как следует не разглядим). Поэтому Ðb, как легко видеть, будет значительно меньше, чем на рис. 17.3, так как F₂ < d₀ (рис. 17.4). Ясно, что глаз при этом придется отодвинуть от края трубы.

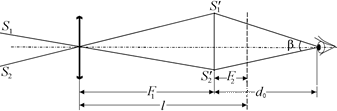
Рис. 17.4

Читатель: А что мы увидим в такую трубу, если оставим на месте окуляр, а объектив заменим обычным стеклом с каким-либо рисунком?

Автор: В этой ситуации мы будем просто смотреть через собирающую линзу (окуляр) на удаленный предмет – «стекло с рисунком».Если мы немного отодвинем глаз от окуляра, то увидим действительное перевернутое уменьшенное изображение А¢В¢ рисунка АВ на стекле (рис. 17.5).

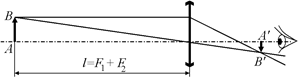
Рис. 17.5

Читатель: При расчете углового увеличения трубы Кеплера мы предполагали, что мнимое изображение А¢¢В¢¢ (см. рис. 17.1) мы «отправили» на бесконечность. А если мы захотим рассматривать его с расстояния наилучшего зрения?

Автор: В этом случае действительное изображение удаленного объекта все равно получится в задней фокальной плоскости объектива. А вот мнимое изображение А¢¢В¢¢ этого действительного изображения получится на расстоянии наилучшего зрения d₀ = 25 см от окуляра (рис. 17.6).

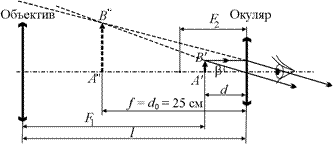
Рис. 17.6

Запишем формулу линзы для окуляра:

.

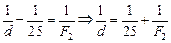Из последнего равенства следует, что 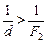, а значит, d < F₂.

Как видно из рис. 17.6, при этом l = F₁ + d < F₁ + F₂, а угол b будет несколько больше, чем на рис. 17.3, поскольку d < F₂.

СТОП! Решите самостоятельно: А1, А2, В1–В3, С1, С2.

Читатель: А можно ли с помощью трубы Кеплера (и микроскопа тоже) получить изображение на экране?

Автор: Можно. Для этого надо, чтобы окуляр давал действительное изображение. Этого можно добиться, если выдвинуть окуляр немного вперед, чтобы действительное изображение А¢В¢, созданное объективом, оказалось за передней фокальной плоскостью окуляра (рис. 17.7).

Заметим, что изображение А¢¢В¢¢ – прямое. Связь между величинами d, f и F₂ определяется формулой

.

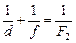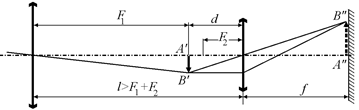
Рис. 17.7

СТОП! Решите самостоятельно: С3.

Телескопы

Труба Кеплера была одним из первых телескопов – зрительных приборов для наблюдения ночного неба. Современные телескопы, использующие в качестве принципиальной схемы трубу Кеплера, называются рефракторами.

Читатель: Я знаю, что современные рефракторы имеют очень большие размеры. Понятно, что чем больше фокусное расстояние объектива, тем больше угловое увеличение телескопа, поэтому они такие длинные. Но зачем делать очень широкие объективы (больше метра в диаметре)? Разве угловое увеличение от этого как-то зависит?

Автор: Нет, конечно. Но будучи «нацеленным» на какой-либо очень слабо светящийся небесный объект, такой телескоп соберет гораздо больше световой энергии, чем телескоп с маленьким объективом. В результате человеческий глаз сможет увидеть такую «слабую» звездочку, которую невозможно «увидеть» с помощью телескопа с маленьким объективом.

Заметим также, что наряду с телескопами-рефракторами используются и телескопы-рефлекторы (отражатели). Принципиальная схема такого телескопа показана на рис. 17.8. Попробуйте разобраться с ней сами.

Рис. 17.8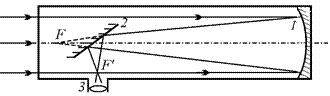

СТОП! Решите самостоятельно: А3, В5.