Можно ли через трубу Кеплера рассматривать
Не слишком удаленные предметы?
Допустим, что мы хотим хорошенько разглядеть какой-то относительно близко расположенный предмет. С помощью трубы Кеплера это вполне возможно. В этом случае изображение, даваемое объективом, получится немного дальше задней фокальной плоскости объектива. А окуляр следует расположить так, чтобы это изображение оказалось в передней фокальной плоскости окуляра (рис. 17.9) (если мы хотим вести наблюдения, не напрягая зрения).
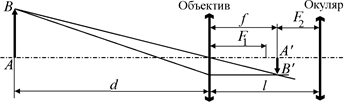
Рис. 17.9
Задача 17.1. Труба Кеплера установлена на бесконечность. После того как окуляр этой трубы отодвинули от объектива на расстояние Dl = 0,50 см, через трубу стали ясно видны предметы, расположенные на расстоянии d. Определить это расстояние, если фокусное расстояние объектива F1 = 50,00 см.
| Dl = 0,50 см F1 = 50,00 см | Решение. В начальный момент расстояние от объектива до действительного изображения предмета, созданного объективом, было равно фокусному расстоянию объектива F1 = 50,00 см. После |
| d = ? | |
того как объектив передвинули, это расстояние стало равно
f = F1 + Dl = 50,00 см + 0,50 см = 50,50 см.
Запишем формулу линзы для объектива:
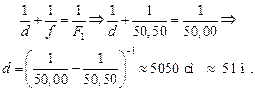
Ответ: d » 51 м.
СТОП! Решите самостоятельно: В4, С4.
Труба Галилея
Первая зрительная труба была сконструирована все-таки не Кеплером, а итальянским ученым, физиком, механиком и астрономом Галилео Галилеем (1564–1642) в 1609 г. В трубе Галилея в отличие от трубы Кеплера окуляр представляет собой не собирающую, а рассеивающую линзу, поэтому и ход лучей в ней более сложный (рис. 17.10).
Лучи, идущие от предмета АВ, проходят через объектив – собирающую линзу О1, после чего они образуют сходящиеся пучки лучей. Если предмет АВ – бесконечно удаленный, то его действительное изображение ab должно было бы получиться в фокальной плоскости объектива. Причем это изображение получилось бы уменьшенным и перевернутым. Но на пути сходящихся пучков стоит окуляр – рассеивающая линза О2, для которой изображение ab является мнимым источником. Окуляр превращает сходящийся пучок лучей в расходящийся и создает мнимое прямое изображение А¢В¢.
Рис. 17.10 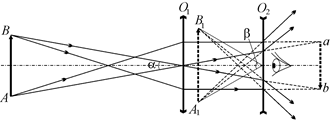
Угол зрения b, под которым мы видим изображение А1В1, явно больше угла зрения a, под которым виден предмет АВ невооруженным глазом.
Читатель: Как-то уж очень мудрёно… А как тут подсчитать угловое увеличение трубы?
Автор: Давайте разберемся по порядку. Забудем на время про рассеивающую линзу. Пусть у нас есть только удаленный предмет АВ и объектив – собирающая линза (рис. 17.11).
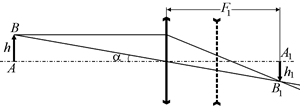 Рис. 17.11
Рис. 17.11
Объектив дает действительное изображение А1В1 в фокальной плоскости. Теперь вспомним про окуляр – рассеивающую линзу, для которой изображение А1В1 является мнимым источником.
Построим изображение этого мнимого источника (рис. 17.12).
1. Проведем луч В1О через оптический центр линзы – этот луч не преломляется.
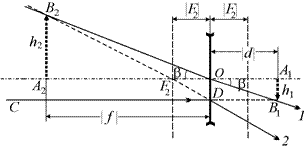 Рис. 17.12
Рис. 17.12
2. Проведем из точки В1 луч В1С, параллельный главной оптической оси. До пересечения с линзой (участок CD) – это вполне реальный луч, а на участке DВ1 – это чисто «умственная» линия – до точки В1 в реальности луч CD не доходит! Он преломляется так, что продолжение преломленного луча проходит через главный передний фокус рассеивающей линзы – точку F2.
Пересечение луча 1 с продолжением луча 2 образуют точку В2 – мнимое изображение мнимого источника В1. Опуская из точки В2 перпендикуляр на главную оптическую ось, получим точку А2.
Теперь заметим, что угол, под которым из окуляра видно изображение А2В2 – это угол А2ОВ2 = b. Из DА1ОВ1 угол 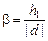 . Величину |d| можно найти из формулы линзы для окуляра: здесь мнимый источник дает мнимое изображение в рассеивающей линзе, поэтому формула линзы имеет вид:
. Величину |d| можно найти из формулы линзы для окуляра: здесь мнимый источник дает мнимое изображение в рассеивающей линзе, поэтому формула линзы имеет вид:
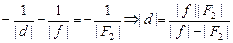 .
.
Если мы хотим, чтобы наблюдение можно было вести без напряжения глаза, мнимое изображение А2В2 надо «отправить» на бесконечность: | f | ® ¥. Тогда из окуляра будут выходить параллельные пучки лучей. А мнимый источник А1В1 для этого должен оказаться в задней фокальной плоскости рассеивающей линзы. В самом деле, при | f | ® ¥
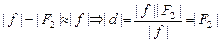 .
.
Этот «предельный» случай схематически изображен на рис. 17.13.
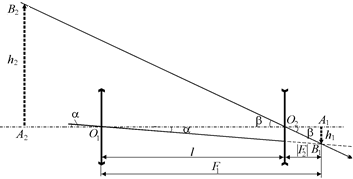
Рис. 17.13
Из DА1О1В1
h1 = F1a, (1)
Из DА1О2В1
h1 = |F1|b, (2)
Приравняем правые части равенств (1) и (2), получим
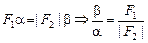 .
.
Итак, мы получили угловое увеличение трубы Галилея
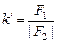 . (17.13)
. (17.13)
Как видим, формула очень похожа на соответствующую формулу (17.2) для трубы Кеплера.
Длина трубы Галилея, как видно из рис. 17.13, равна
l = F1 – |F2|. (17.14)
Задача 17.2. Объективом театрального бинокля служит собирающая линза с фокусным расстоянием F1= 8,00 см, а окуляром – рассеивающая линза с фокусным расстоянием F2= –4,00 см. Чему равно расстояние между объективом и окуляром, если изображение рассматривается глазом с расстояния наилучшего зрения? На сколько нужно переместить окуляр для того, чтобы изображение можно было рассматривать глазом, аккомодированным на бесконечность?
| F1= 8,00 см F2= –4,00 см d0 = 25,0 см | Решение. С помощью бинокля рассматриваются удаленные предметы, находящиеся на расстоянии, много большем F1, поэтому можно считать, что первое изображение S1, даваемое объективом, находится в его фокальной плоскости (рис. 17.14). |
| l = ? Dl = ? | |
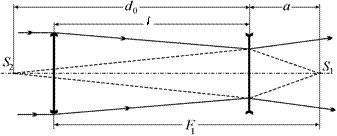
Рис. 17.14
Это изображение играет по отношению к окуляру роль мнимого источника, находящегося на расстоянии а за плоскостью окуляра. Мнимое изображение S2, даваемое окуляром, находится на расстоянии d0 перед плоскостью окуляра,где d0 – расстояние наилучшего зрения нормального глаза.
Запишем формулу линзы для окуляра:
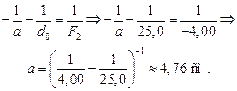
Расстояние между объективом и окуляром, как видно из рис. 17.14, равно
l = F1 – a = 8,00 – 4,76 » 3,24 см.
В том случае, когда глаз аккомодирован на бесконечность, длина трубы по формуле (17.4) равна
l1 = F1 – |F2| = 8,00 – 4,00 » 4,00 см.
Следовательно, смещение окуляра составляет
Dl = l – l1 = 4,76 – 4,00 » 0,76 см.
Ответ: l » 3,24 см; Dl » 0,76 см.
СТОП! Решите самостоятельно: В6, С5, С6.
Читатель: А может ли труба Галилея дать изображение на экране?
Автор: Может! Для этого надо, чтобы окуляр (рассеивающая линза) дал действительное изображение.
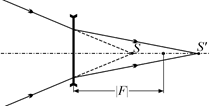 Рис. 17.15
Рис. 17.15
|
Мы знаем, что рассеивающая линза может дать действительное изображение только в одном случае: если мнимый источник находится за линзой перед задним фокусом (рис. 17.15).
Задача 17.3. Объектив трубы Галилея дает в фокальной плоскости действительное изображение Солнца. При каком расстоянии между объективом и окуляром можно получить на экране изображение Солнца с диаметром, в три раза бóльшим, чем у действительного изображения, которое получилось бы без окуляра. Фокусное расстояние объектива F1 = 100 см, окуляра – F2 = –15 см.
| F1 = 100 см F2 = –15 см D1/D = 3 | Решение. Собирающая линза (объектив) создала бы действительное изображение А1В1 (рис. 17.16), если бы не было рассеивающей линзы (окуляра). Для рассеивающей линзы отрезок А1В1 является мнимым источником. |
| l = ? | |

Рис. 17.16
Рассеивающая линза создает на экране действительное изображение этого мнимого источника – отрезок А2В2. На рисунке R1 – радиус действительного изображения Солнца на экране, а R – радиус действительного изображения Солнца, созданного только объективом (при отсутствии окуляра).
Из подобия DА1ОВ1 и DА2ОВ2 получим:
 .
.
Запишем формулу линзы для окуляра, при этом учтем, что d < 0 – источник мнимый, f > 0 – изображение действительное:
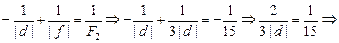 |d| = 10 см.
|d| = 10 см.
Тогда из рис. 17.16 находим искомое расстояние l между окуляром и объективом:
l = F1 – |d| = 100 – 10 = 90 cм.
Ответ: l = 90 см.
СТОП! Решите самостоятельно: С7, С8.
Дата добавления: 2016-04-11; просмотров: 2457;
