Непосредственный подсчет вероятностей событий

Способы определения вероятностей событий

Основные понятия

Теория вероятностей является математической наукой, изучающей закономерности поведения случайных событий, случайных величин и случайных процессов. Случайным событием называют такое событие, которое при определенных условиях может происходить, а может и не происходить.

Например: 1 Попадание баскетбольного мяча в корзину.

2 Поражение мишени при стрельбе из пистолета.

3 Продолжительность работы некоторых однотипных приборов, изделий и др.

События подразделяют на следующие виды: достоверные, возможные (случайные) и невозможные.

Вероятностью случайного события называют численную меру степени объективной возможности появления этого события.

Событие, которое в результате опыта обязательно произойдет, относят к достоверным событиям. Вероятность достоверного события принимается равной единице.

Невозможное событие в результате опыта произойти не может, поэтому вероятность его появления считается равной нулю.

Например. Вынуть белый шар из урны с красными шарами – событие невозможное; вынуть красный шар из этой же урны – событие достоверное.

Следовательно, вероятность случайного события 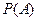численно определяется значениями между нулем и единицей, т.е.

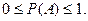
Несколько событий образуют полную группу, если при проведении опыта появится хотя бы одно из них.

Например. По мишени производится три выстрела. А₀ - событие, что в мишень не попадает ни одна пуля. А₁ – событие, что в мишень попадает одна пуля. А₂ - событие, что в мишень попадает две пули. А₃ - событие, что в мишень попадает три пули.

События А₀ А₁ А₂ А₃ образуют полную группу событий.

Если в одном и том же опыте появление одного события исключает появление других событий, то такие события называют несовместными. Кроме того события могут быть равновозможными и не равновозможными событиями. Несколько событий в данном опыте называют равновозможными, если ни одно из них объективно не может появляться чаще других.

Кроме приведенных понятий часто применяют понятие благоприятный случай. Случай называют благоприятным для появления данного события, если появление этого случая влечет за собой появление интересующего события.

При выборе способа расчета вероятности событий используют понятие схема случаев. Если при проведении опыта все исходы равновероятны, несовместны и образуют полную группу событий, то в этом случае опыт сводится к схеме случаев.

К способам определения вероятностей относят:

а) непосредственный подсчет вероятностей;

б) статистический способ определения вероятностей;

в) геометрический способ определения вероятностей;

г) определение вероятностей одних событий через известные вероятности других событий путем составления равенств.

Непосредственный подсчет вероятностей событий

Данный способ применяется в том случае, если опыт сводится к схеме случаев. Тогда вероятность события A определяется как отношение числа благоприятных случаев этому событию к общему числу равновозможных и несовместных исходов опыта, составляющих полную группу событий, т.е.

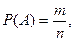
где m – число исходов, благоприятных событию;

n – число всех равновозможных и несовместных исходов опыта.

Пример 1: В ящике имеются 4 транзистора, из них 1 транзистор неисправен. Какова вероятность того, что взятый наугад транзистор будет исправным?

Решение.

A – событие того, что в результате опыта взятый наугад транзистор будет исправным.

P(A) - вероятность события A.

Так как опыт сводится к схеме случаев, число исходов конечно и m=3 , а n=4, то

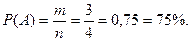
Как понимать этот результат?

Только при многократном повторении опыта в 75% случаев будет браться исправный транзистор.

Пример 2:В условиях примера 1 наугад берутся два транзистора. Требуется определить вероятность того что, что оба будут исправны.

Обозначим. B – событие соответствующее тому, что оба взятых транзистора будут исправны. P (B) - вероятность события B.

Для подсчета вероятности события обозначим транзисторы в ящике: Н – неисправный транзистор; И(1), И(2), И(3) - исправные транзисторы, и составим таблицу размещения их из 4 элементов по 2 элемента.

Таблица 1

Из таблицы легко определить числа: m=6, n=12. Откуда вероятность события B будет равна P(B)=m/n=6/12=0,5.

Вместе с этим исходы, показанные в таблице, можно толковать как размещения или как сочетания из 4 элементов по 2 т.е.

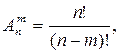
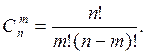
Через размещения вероятность события B можно определить следующим образом:

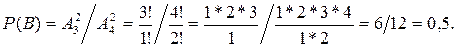
С помощью сочетаний вероятность события B определяется как

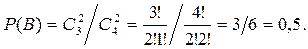
Классическим определением вероятности пользуются лишь в том случае, когда можно произвести непосредственный подсчет тех и других случаев, т.е. когда число исходов конечно. Однако на практике встречаются испытания, число возможных исходов которых бесконечно. Кроме того, часто невозможно представить исходы испытания в виде равновозможных и несовместных событий.