Теорема гипотез (формула Байеса)
Постановка задачи. Пусть событие A может произойти только совместно с одним из следующих событий: 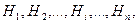 которые являются несовместными между собой и составляют полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
которые являются несовместными между собой и составляют полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
Провели испытание, и событие A произошло. Какая из гипотез вероятнее всего реализовалась?
Чтобы ответить на поставленный вопрос, необходимо определить условную вероятность гипотезы 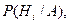 где i – 1,2,…,n.
где i – 1,2,…,n.
Согласно теореме умножения вероятностей
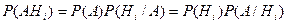 . Откуда условная вероятность гипотезы будет равна
. Откуда условная вероятность гипотезы будет равна
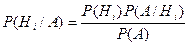 , где P(A) – полная вероятность.
, где P(A) – полная вероятность.
В общем случае формула Байеса запишется в виде
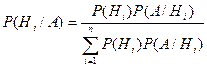 ,
,
где 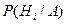 - вероятность гипотезы после испытания, давшего событие A;
- вероятность гипотезы после испытания, давшего событие A;
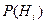 - вероятность гипотезы до испытания.
- вероятность гипотезы до испытания.
Формула Байеса применяется при решении практических задач, когда событие A произошло и требуется произвести количественную переоценку вероятностей событий 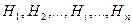 .
.
Априорные (до опыта) вероятности 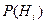 известны, и требуется вычислить апостериорные (после опыта) вероятности
известны, и требуется вычислить апостериорные (после опыта) вероятности 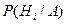 .
.
Пример 2: Неисправность в первом блоке передатчика влечет понижение выходной мощности с вероятностью 0,6, а неисправность во втором блоке - с вероятностью 0,2. Надежность работы первого (второго) блока характеризуется вероятностью 0,7 (0,3).
Какой из блоков необходимо проверить на исправность в первую очередь, если зафиксировано падение выходной мощности?
Решение.
Для ответа на этот вопрос необходимо вычислить условные вероятности гипотез: 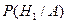 ,
, 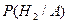 ,
,
где A – событие падения выходной мощности;
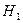 - событие неисправности в первом блоке;
- событие неисправности в первом блоке;
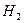 - событие неисправности во втором блоке.
- событие неисправности во втором блоке.
Из условия задачи априорные вероятности гипотез будут равны
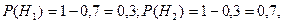 а условные вероятности события A -
а условные вероятности события A - 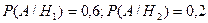 .
.
Тогда апостериорные вероятности определяются по формуле Байеса, т.е.
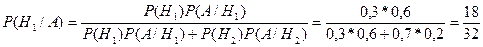 ,
,
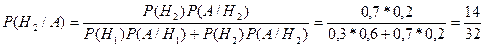 .
.
Вывод: в первую очередь необходимо проверить первый блок передатчика, так как 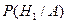 больше, чем
больше, чем 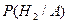 .
.
Дата добавления: 2016-04-19; просмотров: 787;
