Повторение испытаний

На практике часто приходится иметь дело с сериями независимых опытов, в каждом из которых некоторое событие A может появиться или нет. При этом вероятность появления его в каждом опыте известна и она не меняется от опыта к опыту.

Примеры: появление изделий с браком в процессе производства; поступление на вход приемника серии импульсов, отраженных целью. Появление каждого импульса можно рассматривать как опыт, в результате которого импульс либо проходит на выход приемника, либо не проходит из-за помех.

В общем случае задача состоит в том, чтобы определить вероятность появления события A ровно m раз в n опытах и не появления n-m раз. Условимся считать, что вероятность события A в каждом опыте одна и та же и равна p. Следовательно, вероятность не наступления события A в каждом опыте постоянна и равна q=1-p.

Вероятность одного сложного события, состоящего в том, что в n опытах событие A наступит m раз и не наступит n-m раз равна 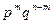( на основании теоремы умножения вероятностей независимых событий).

Так как не требуется, чтобы событие A повторилось ровно m раз в определенной последовательности, то таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m,т.е. 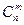. Поскольку эти сложные события несовместны и их вероятности одинаковы, то искомая вероятность будет равна

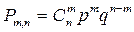, где .

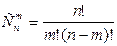Полученное выражение называют формулой Бернулли.

Пример 3:Пусть n=2: .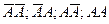

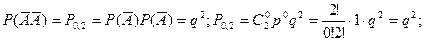
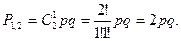
Так как 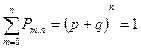, то можно определить вероятность появления события не менее m раз по следующему выражению

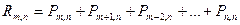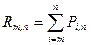, или , или .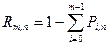

В частном случае, когда m=1 получают формулу вероятности появления события хотя бы один раз .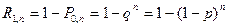

При большом числе опытов n пользоваться приведенными выше формулами неудобно, поэтому используют формулу Лапласа – Гаусса

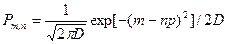, где D=n p q.

Вопросы для повторения

1 Каким образом определяется вероятность события при способе непосредственного подсчета?

2 Что называется статистической вероятностью?

3 Какую группу событий называют полной? Приведите пример.

4 При каких условиях опыт относится к схеме случаев?

5 Какие события называются зависимыми, а какие нет? Приведите примеры зависимых и независимых событий.

6 Чему равна вероятность произведения двух событий (зависимых и независимых)?

7 Чему равна вероятность суммы двух событий ( совместных и несовместных)?

8 Что называется условной вероятностью?

9 Как записывается формула полной вероятности? Докажите ее.

10 Как записывается формула Байеса? Выведите ее.

11 Придумайте задачи на применение формулы полной вероятности и формулы Байеса.

12 Объясните, как рассчитать:

вероятность появления события A ровно m раз в n независимых опытах?

вероятность появления события A не менее m раз в n независимых опытах?

вероятность появления события A хотя бы один раз в n независимых опытах?

13 Какая теорема позволяет рассчитывать эти вероятности тем точнее, чем больше n.

Упражнения

1.1 При бросании игральной кости требуется определить вероятность появления числа делящегося на два.

1.2 Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».

1.2 В ящике 100 деталей, из них 10 бракованных. Наудачу извлекаются четыре детали. Найти вероятность того, что среди извлеченных деталей нет бракованных.

1.4 ОТК обнаружила 5 бракованных книг из партии в 100 случайно отобранных книг. Найти вероятность появления бракованных книг.

1.5 Найти вероятность попадания в мишень одним из двух стрелков при одновременном залпе обоих, если вероятность поражения мишени первым стрелком равна 0,7, а вторым – 0,8.

1.6 В семье 5 детей. Найти вероятность того, что среди них два мальчика, если известно, что вероятность рождения мальчика равна 0.51.

1.7 Монета брошена три раза. Определить вероятность того, что хотя бы один раз появится герб.

1.8 Из партии в 20 телевизоров 5 телевизоров неисправны. Для проверки отобрано 3 телевизора. Найти вероятность того, что в число отобранных войдут только два исправных телевизора.

1.9 Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого из элементов одинакова и равна 0.1. Найти вероятность того, что не откажет ни один элемент.

1.10 Найти вероятность того, что событие A появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события A в одном испытании равна 0.4.

1.11 Вероятность хотя бы одного попадания в цель при 4-х выстрелах равна 0.9984. Найти вероятность попадания в цель при одном выстреле.

1.12 Определить вероятность ровно двух попаданий в мишень при пяти выстрелах, если вероятность попадания при каждом выстреле равна 0,6.