Вероятность суммы событий

Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем

P(A+B) = P(A) + P(B). (3.6)

Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т.к. легко выводится из классического определения вероятности (доказать самостоятельно).

Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение. Введем следующие события: B={появление хотя одного туза}, A₁={появление одного туза}, A₂={появление двух тузов}, A₃={появление трех тузов}. Очевидно, что B=A₁+A₂+A₃. Поскольку события A₁, A₂ и A₃.несовместны, то

P(B) = P(A₁)+P(A₂)+P(A₃) =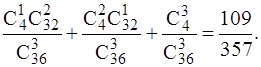

Эту задачу можно решить иначе. Событие 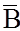, противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. Поскольку P(B)+P( 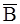)=1, то

P(B) = 1 – P( ) =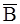

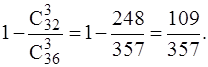
Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде

A+B = A+B 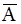и B = B 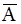+BA.

(объясните эти равенства, используя диаграммы Вьенна). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то

P(A+B) = P(A) + P(B 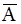), P(B) = P(B 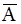)+P(BA).

Исключая P(B 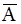), получим

P(A+B) = P(A)+P(B)–P(AB). (3.7)

Это равенство известно как теорема сложения вероятностей совместных событий.

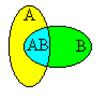
Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых S_A+B=S₁+S₂+S_AB, где S₁ соответствует событию А–АВ, а S₂ – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью S_А= S₁+S_АВ, а событию В – S_В= S₂+S_АВ. В результате получим, что S_А+В= S_А+S_В–S_АВ. Полученное равенство соответствует теореме сложения вероятностей.

Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. В частности,

P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8)

Докажите данную формулу самостоятельно.

Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?

Решение. Пусть A₁={первый стрелок попал по цели}, A₂={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А₁+А₂. Поскольку события А₁ и А₂ совместны, но независимы, то

P(А₁+А₂) = P(А₁)+P(А₂)–P(А₁)P(А₂) = 0,7+0,8–0,7×0,8 = 0,94.

Отметим, что событие В можно записать также в виде A₁ 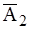+ A₂+A₁A₂. Тогда получим

P(B) = P(A₁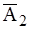)P( )+P( )P(A₂)+P(A₁)P(A₂) =
= 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.

Однако такой путь слишком длинный.

Пример 3.7. Дана электрическая цепь:

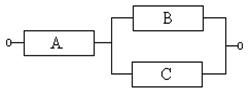
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдет из строя элемент А, или сразу два элемента В и С. При помощи алгебры событий разрыв цепи можно описать следующим образом: 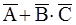. Поскольку эти события совместные и независимые, то получим

= .

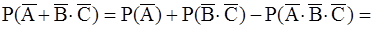
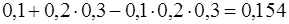3.3. Вероятность появления хотя бы одного
события

В жизни, производстве часто возникают такие ситуации, когда нужно вычислить вероятность появления хотя бы одного события из некоторого набора возможных событий. Например, если по цели был сделан залп из нескольких орудий, то интерес представляет вероятность того, что цель будет поражена, т.е. что будет хотя бы одно попадание.

Математически такую схему событий можно представить следующим образом. Пусть имеется n независимых событий A₁, A₂, ..., A_n, причем известны вероятности каждого из этих событий. Пусть A – появление хотя бы одно из этих событий, тогда противоположное событие  означает, что ни одно из этих событий не появится. Поскольку P(A)=1–P()=1–P(₁₂..._n)=1–P(₁)P(₂)...P(_n), то вероятность появления хотя бы одного из событий A₁,A₂,...,A_n равна

P(A₁+A₂+...+A_n) = 1– P(₁)P(₂)...P(_n). (3.9)

Если события A_i равновероятны, то можно положить P(₁)=P(₂)= ... =P(_n)=q. Тогда формула (9) примет следующий вид:

P(A₁+A₂+...+A_n) = 1– qⁿ (3.10)

Пример 3.8. Вероятности попадания в цель при стрельбе из трех орудий таковы: p₁=0,8, p₂=0,7, p₃=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Решение. Поскольку вероятности попаданий независимы и q₁=1–p₁=0,2, q₂=1–p₂=0,3, q₃=1–p₃=0,1, то искомая вероятность равна

P(A) = 1–q₁q₂q₃ = 1–0,006 = 0,994.

Пример 3.9. Вероятность того, что при одном выстреле стрелок попадет в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Вероятность попадания хотя бы один раз при n выстрелах равна:

P(A) = 1–qⁿ.

Поскольку P(A)³0,9 и q=1–p=0,6, то

1–0,6ⁿ ³ 0,9 Þ 0,6ⁿ £ 0,1 Þ nlg0,6 £ lg0,1 Þ

Þ .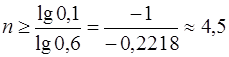

Таким образом, чтобы хотя бы один раз попасть в цель с вероятностью не менее 0,9 стрелок должен произвести не менее 5 выстрелов.