Вероятность безотказной работы (ВБР)
Статистическая оценка ВБР (эмпирическая функция надежности) определяется:
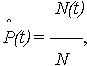
| (1) |
отношением числа N(t) объектов, безотказно проработавших до момента наработки t, к числу объектов, исправных к началу испытаний (t = 0) - к общему числу объектов N. Оценку ВБР можно рассматривать как показатель доли работоспособных объектов к моменту наработки t.
Поскольку N(t) = N - n(t), то ВБР по (1)
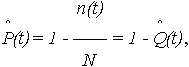
| (2) |
где 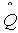 (t) = n(t)/ N – оценка вероятности отказа (ВО).
(t) = n(t)/ N – оценка вероятности отказа (ВО).
В статистическом определении оценка ВО представляет эмпирическую функцию распределения отказов.
Так как события, заключающиеся в наступлении или не наступлении отказа к моменту наработки t, являются противоположными, то
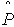 (t)+ (t)+ 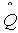 (t) = 1 (t) = 1
| (3) |
Нетрудно убедиться, что ВБР является убывающей, а ВО – возрастающей функцией наработки. Действительно
- в момент начала испытаний t = 0 число работоспособных объектов равно общему их числу N(t) = N(0) = N, а число отказавших - n(t) = n(0) = 0, поэтому 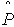 (t) =
(t) = 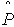 (0) = 1, а
(0) = 1, а 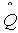 (t) =
(t) = 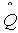 (0) = 0;
(0) = 0;
- при наработке t 
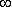 все объекты, поставленные на испытания, откажут, т. е. N(
все объекты, поставленные на испытания, откажут, т. е. N( 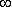 ) = 0, а n(
) = 0, а n( 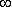 ) = N, поэтому
) = N, поэтому 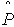 (t) =
(t) = 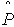 (
( 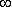 ) = 0, а
) = 0, а 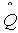 (t) =
(t) = 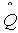 (
( 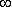 ) = 1.
) = 1.
Вероятностное определение ВБР
P(t) = P{T 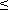 t}. t}.
| (4) |
Таким образом, ВБР есть вероятность того, что случайная величина наработки до отказа T окажется не меньше некоторой заданной наработки t.
Очевидно, что ВО будет являться функцией распределения случайной величины T и представляет из себя вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:
| Q(t) = P{T < t}. | (5) |
Графики ВБР и ВО приведены на рис. 1.
В пределе, с ростом числа N (увеличение выборки) испытываемых объектов, 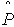 (t) и
(t) и  (t) сходятся по вероятности (приближаются по значениям) к P(t) и Q(t).
(t) сходятся по вероятности (приближаются по значениям) к P(t) и Q(t).
Сходимость по вероятности представляется следующим образом:

| (6) |
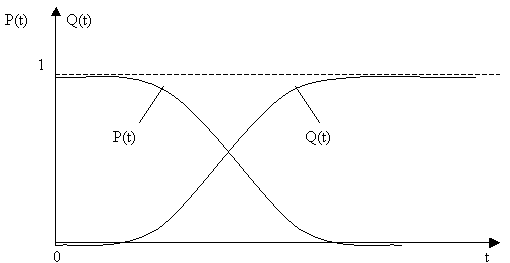
Рис. 1
Практический интерес представляет определение ВБР в интервале наработки [t, t + 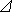 t], при условии, что объект безотказно проработал до начала t интервала.Определим эту вероятность, используя теорему умножения вероятностей, и выделив следующие события:
t], при условии, что объект безотказно проработал до начала t интервала.Определим эту вероятность, используя теорему умножения вероятностей, и выделив следующие события:
A = {безотказная работа объекта до момента t};
B = {безотказная работа объекта в интервале 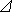 t};
t};
C = A·B = {безотказная работа объекта до момента t + 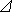 t}.
t}.
Очевидно P(C) = P(A·B) = P(A)·P(B| A), поскольку события A и B будут зависимыми.
Условная вероятность P(B| A) представляет ВБР P(t, t + 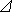 t) в интервале [t, t +
t) в интервале [t, t + 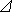 t], поэтому
t], поэтому
P(B| A) = P(t, t + 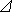 t) = P(C)/ P(A) = P(t + t) = P(C)/ P(A) = P(t + 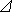 t)/ P(t). t)/ P(t).
| (7) |
ВО в интервале наработки [t, t + 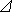 t], с учетом (7), равна:
t], с учетом (7), равна:
Q( t, t + 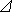 t ) = 1 - P( t, t + t ) = 1 - P( t, t + 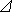 t ) = [ P(t ) - P(t + t ) = [ P(t ) - P(t +  t ) ] / P(t ). t ) ] / P(t ).
| (8) |
Дата добавления: 2016-03-20; просмотров: 890;
