Формула полной вероятности. На практике часто возникают ситуации, когда требуется определить вероятность события, которое может произойти только с одним из событий
На практике часто возникают ситуации, когда требуется определить вероятность события, которое может произойти только с одним из событий, образующих полную группу. Например, требуется проверить качество деталей, расположенных по нескольким ящикам; оценить надежность прибора, который может работать в нескольких режимах, и т.д.
Теорема. Если событие А может осуществляться только при выполнении одного из событий В1, В2, ... , Bn, которые образуют полную группу несовместных событий, то P(A) вычисляется по формуле:
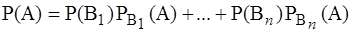 , (3.11)
, (3.11)
которая называется формулой полной вероятности.
Доказательство. Согласно условию теоремы, событие А может наступить, если появится одно из событий B1, B2, ... , Bn. Это означает, что появление события А влечет появление одного из следующих событий: B1A, B2A, ... , BnA, неважно какого. По этому событие А можно представить в виде A= B1A+B2A+...+BnA. Так как события B1, B2, ... , Bn несовместны, то, очевидно, что несовместны и события B1A, B2A, ... , BnA. Тогда применяя теорему сложения вероятностей несовместных событий, получим
P(A) = P(B1A)+P(B2A)+...P(BnA).
Далее, в соответствии с теоремой умножения вероятностей, получим формулу полной вероятности (11).
Пример 3.10. Партия деталей изготовлена двумя рабочими. Первый изготовил 2/3 деталей партии, второй – 1/3. Вероятность брака для первого рабочего равна 1%, для второго – 10%. На контроль взяли одну деталь. Какова вероятность того, что она бракованная?
Решение. Пусть А – событие, состоящее в том, что взятая наудачу деталь бракованная. Здесь возможны два случая: 1) деталь изготовлена первым рабочим (событие В1), 2) деталь изготовлена вторым рабочим (событие В2). Очевидно, что события В1 и В2 несовместны и образуют полную группу. Их вероятности, по условию, равны
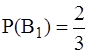 и
и 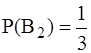 .
.
Условные вероятности события А равны
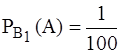 и
и 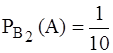 .
.
Следовательно, по формуле полной вероятности, находим вероятность того, взятая деталь будет бракованной:
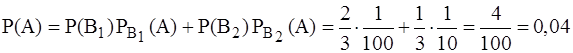 .
.
Пример 3.11. В первой урне находится 5 белых и 3 черных шара. Во второй – 4 белых и 5 черных шара. Из первой урны во вторую наугад перекладывают два шара. После этого из второй урны вынимают сразу 4 шара. Какова вероятность того, что шары будут одного цвета?
Решение. результат второго испытания (т.е. вынимание шаров из второй урны) зависит от того, какие шары были переложены из первой урны. Здесь возможны три случая:
B1 = {оба шара белые},
B2 = {оба шара черные},
B3 = {один белый, один черный шар}.
Очевидно, что события B1, B2 и B3 несовместны и образуют полную группу. Их вероятности равны
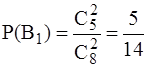 ,
, 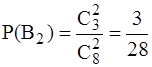 ,
, 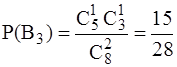 .
.
Условные вероятности события А={шары одного цвета}, равны
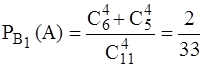 ,
, 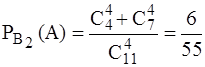 ,
,
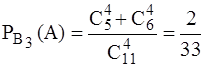 .
.
Применяя формулу полной вероятности, получим
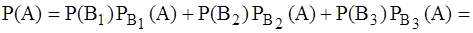
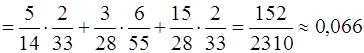 .
.
Формула Байеса
Во многих приложениях теории вероятностей встречается следующая задача. Перед началом эксперимента имеется несколько предположений (несовместных гипотез) для объяснения некоторого опыта. Вероятности этих гипотез могут быть определены приблизительно, исходя из каких-либо соображений, порой даже интуитивных. После эксперимента получают дополнительную информацию, на основании которой производят переоценку первоначальных гипотез.
При выводе полной вероятности предполагалось, что событие А, вероятность которого следовало определить, могло произойти с одним из событий B1, B2, ... , Bn, образующих полную группу несовместных событий (гипотез), при этом вероятности указанных событий известны заранее. Предположим, что проведен опыт и событие А наступило. Установим, как изменятся после этого вероятности гипотез, т.е. найдем условную вероятность PA(Bi) для каждой из гипотез. По теореме умножения вероятностей можно написать
P(ABi) = P(A)PA(Bi) = 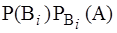 .
.
Из последнего равенства получим
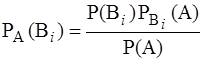 . (3.12)
. (3.12)
Применяя для P(A) формулу полной вероятности, получим
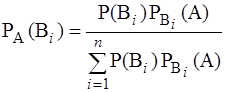 . (3.13)
. (3.13)
Полученная формула называется формулой Байеса, или теоремой переоценки гипотез. В настоящее время, эпоху компьютеризации, формула Байеса находит широкое применение при решение проблем управления в экономике и промышленности, связанных с недостаточной информацией. По мере поступления информации и ее накопления проводится корректировка различных решений и планов.
Пример 3.12. Двое стрелков произвели по одному выстрелу по мишени. Вероятность попадания первым стрелком равна 0,8, вторым – 0,4. Мишень поражена одним попаданием. Определить вероятность того, что в мишень попал первый стрелок?
Решение. До стрельбы возможны следующие предположения (гипотезы):
| B1 = {оба стрелка не попали}, B2 = {оба стрелка попали}, B3 = {попал только первый стрелок}, B4 = {попал только второй стрелок}, | P(B1) = 0,2×0,6 = 0,12, P(B1) = 0,8×0,4 = 0,32, P(B1) = 0,8×0,6 = 0,48, P(B1) = 0,2×0,4 = 0,08. |
Эти события образуют полную группу несовместных событий. Пусть А – поражение мишени одним попаданием, тогда ее вероятность можно найти по формуле полной вероятности:
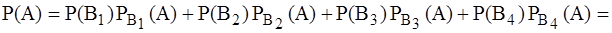
= 0,12×0+ 0,32×0+ 0,48×1+ 0,08×1 = 0,56.
Здесь учтено, что при осуществлении событий В1 и В2 событие А – невозможно, при осуществлении событий В3 и В4 событие А – достоверное. В результате, по формуле Байеса находим:
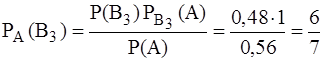 .
.
Дата добавления: 2016-03-10; просмотров: 2513;
