III. Методика измерений и расчетные формулы. Для выполнения работы используется установка ФМ-19, общий вид которой представлен на рис

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА МЕТОДОМ ИЗГИБА

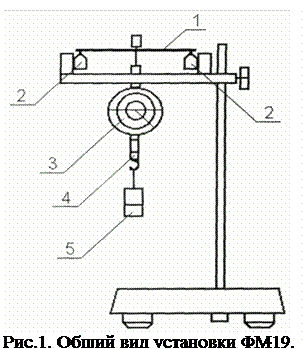Для выполнения работы используется установка ФМ-19, общий вид которой представлен на рис. 1. Основание снабжено регулируемыми опорами и узлом крепления вертикальной стойки, в верхней части которой закреплен кронштейн. Исследуемая пластина 1 помещается на призматические опоры 2, установленные на кронштейне. Там же установлен часовой индикатор 3 для измерения величины прогиба. При измерениях на середину пластины 1 кладется скоба нагружения 4 с наборным грузом 5.

В комплект установки также входят фотодатчик с узлом крепления к стойке и блок электронный ФМ-1/1 (на рис.1 не показаны).

III. Методика измерений и расчетные формулы.

Деформация — это изменение формы и/или размеров тела без изменения массы под действием внешней силы. Разные виды деформации сводятся к двум основным: сжатию-растяжению и сдвигу. При деформации образца в нем возникает сила упругости. Отношение силы упругости к площади поперечного сечения образца называется напряжением. При деформации сжатия- растяжения в образце возникает нормальное напряжение в направлении, перпендикулярном поперечному сечению. Деформация сдвига вызывается силами, направленными по касательной к сечению образца, при этом в образце возникает тангенциальное напряжение.

При малых деформациях 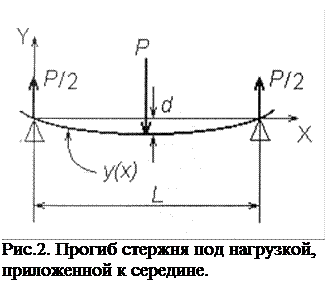справедлив закон Гука: напряжение прямо пропорционально относительной деформации. Коэффициентом пропорциональности для деформации сжатия-растяжения является модуль Юнга, который определяется ка напряжение, возникающее в образце при единичном относительном удлинении (т. е. при увеличении первоначальной длины вдвое).

Деформация изгиба представляет собой неоднородную деформацию сжатия-растяжения.

Прямой упругий стержень, свободно лежащий обоими концами на твердых опорах и нагруженный в середине грузом весом Р,претерпевает деформацию изгиба, как показано на рис. 2. При таком изгибе верхние слои стержня сжимаются, нижние растягиваются, а некоторый средний — нейтральный — слой сохраняет длину и только претерпевает искривление. Перемещение d, которое получает середина стержня, называется стрелой прогиба. Стрела прогиба зависит от величины нагрузки, от формы и размеров стержня, а также от упругих свойств стержня.

Найдем связь между стрелой прогиба и характеристиками упругого стержня. В данной работе используется пластина прямоугольного сечения размерами L (длина), h (высота), b (ширина). Под воздействием внешней силы пластина искривляется, и ее форма может быть описана функцией у(х)(см. рис.2).

Возникающие в пластине силы упругости пропорциональны кривизне пластины, т. е. второй производной у"(х). Условие равновесия имеет вид:

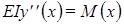, (1)

где E — модуль Юнга, M(x) — изгибающий момент, коэффициент I зависит от формы и размеров пластины.

Величина изгибающего момента определяется по формуле:

.

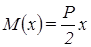Коэффициент I для прямоугольной пластины определяется по формуле:

.

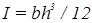Из условия равновесия изогнутой пластины с учетом выражения для изгибающего момента получаем дифференциальное уравнение для формы пластины:

.

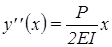После интегрирования имеем:

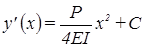. (2)

Константа интегрирования C определяется из условия нулевого наклона пластины в середине:

.

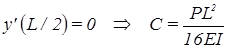После подстановки выражения для C в (2) и интегрирования получаем:

.

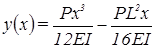Стрела прогиба d равна смещению середины пластины:

.

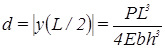Отсюда можно выразить модуль Юнга:

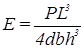. (3)