ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
Эмпирическая функция распределения. По вариационному ряду или выборке легко построить эмпирическую функцию распределения F*(x) - оценку истинной функции распределения F(x) = P(X<x).
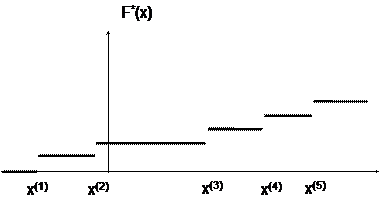 |
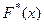 = число точек выборки, лежащих левее т х на оси ох, или
= число точек выборки, лежащих левее т х на оси ох, или
доля точек выборки слева от т. х. Так, 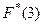 = 0.4 означает, что в выборке 40% чисел имеют значение меньшее трех.
= 0.4 означает, что в выборке 40% чисел имеют значение меньшее трех.
График 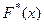 строим так. Двигаясь слева направо вдоль оси ох, на каждой точке х1 ряда рисуем скачок функции, равный 1/n; между любыми соседними точками х1 и х1+1 функция постоянна, т.е. график - кусочно постоянная функция, имеющая ступенчатый вид.
строим так. Двигаясь слева направо вдоль оси ох, на каждой точке х1 ряда рисуем скачок функции, равный 1/n; между любыми соседними точками х1 и х1+1 функция постоянна, т.е. график - кусочно постоянная функция, имеющая ступенчатый вид.
Слева от точки х.( 1) 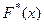 равна О, справа от точки х.(n) - равна 1.
равна О, справа от точки х.(n) - равна 1.
Теорема Гливенко
Советским математиком Гливенко была доказана теорема: При числе испытаний, стремящихся к бесконечности эмпирическая функция распределения равномерно сходится к теоретической функции распределения.
Пример 12. Построить график 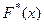 для выборки:
для выборки:
{0.17, 1.53, 0.99, 2.04, 0.56, 1.73, 0.95, 1.25, 0.75, 1.82}, n=10.
Упорядочим выборку: {0.17, 0.56, 0.75, 0.95, 0.99, 1.25, 1.53, 1.73, 1.82, 2.04}, и нанесем точки х( 1) ,х(2) , ... , х(10) на ось х. Высота каждой ступеньки графика равна 1/n = 0.1 и число x n=10 .
Эмпирическая функция 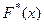 по статистическому распределению строится точно так же, как функция распределения
по статистическому распределению строится точно так же, как функция распределения 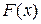 дискретной cл. величины строится по ряду распределения вероятностей.
дискретной cл. величины строится по ряду распределения вероятностей.
Сравним функции 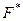 и F. F - неизвестная и неслучайная функция, интересующая исследователя. Функция F содержит всю информацию о соответствующей величине X, ее можно назвать истинной или теоретической функцией и по ней можно найти, в частности, МХ и DХ и другие моменты распределения.
и F. F - неизвестная и неслучайная функция, интересующая исследователя. Функция F содержит всю информацию о соответствующей величине X, ее можно назвать истинной или теоретической функцией и по ней можно найти, в частности, МХ и DХ и другие моменты распределения.
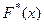 - функция, находимая по случайной выборке и потому случайная.
- функция, находимая по случайной выборке и потому случайная.
С ростом объема n выборки функция 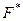 приближается к F и
приближается к F и
при большом n - 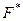 практически совпадает с F.
практически совпадает с F.
При большом числе наблюдений над непрерывной cл. величиной X прибегают к группировке данных: ось х разбивают на 10-15 интервалов 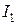 , I2 , . . . ,IК . Пусть
, I2 , . . . ,IК . Пусть  - число наблюдений, попавших в интервал
- число наблюдений, попавших в интервал 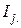
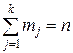 .
.
Длины интервалов не обязательно одинаковы.
По сгруппированным данным выборочное распределение выражают разными графиками, в первую очередь это:
1) кумулятивная кривая распределения (или график накопленной
частоты) - аппроксимация эмпирической функции распределения 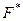 ;
;
2) гистограмма;
3) полигон частот.
Строятся они так.
Кумулятивная кривая. Взяв на оси ох точку 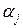 - правый конец интервала
- правый конец интервала 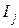 = 1,2,...,к - отложим в ней по оси ординат накопленную частоту
= 1,2,...,к - отложим в ней по оси ординат накопленную частоту 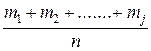 .
.
Построенные точки плоскости соединим последовательно прямолинейными отрезками. В точках 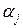 разбиения кумулятивная кривая совпадает с эмпирической функцией распределения
разбиения кумулятивная кривая совпадает с эмпирической функцией распределения 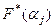 , а между этими точками меняется линейно.
, а между этими точками меняется линейно.
Гистограмма. На каждом интервале Ij оси абсцисс строим прямоугольник с высотой hj = mj/(nIj), обеспечивающей площадь прямоугольника, равную частоте mj/n (здесь lj= 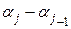 - длина интервала Ij). Вся площадь под графиком гистограммы равна 1. Другой вариант гистограммы получим, если высоту hj берем равной mj , а все длины lj одинаковы.
- длина интервала Ij). Вся площадь под графиком гистограммы равна 1. Другой вариант гистограммы получим, если высоту hj берем равной mj , а все длины lj одинаковы.
Полигон. В середине каждого интервала Ij разбиения строим ординату, равную mj/n - частоте попадания наблюдений в этот интервал. Соединяем полученные точки прямолинейными отрезками.
Другой вариант полигона получим, соединяя отрезками середины верхних сторон прямоугольников, образующих гистограмму.
Гистограмма и полигон являются эмпирическими аналогами плотности вероятности. Если n увеличивать, а длины lj интервалов уменьшать, то гистограмма и полигон неограниченно приближаются к кривой плотности вероятности cл. величины.
Пример 13. Построить три указанные кривые по сгруппированным данным, представленным в таблице 4 частот, n=200.
Таблица Сгруппированные данные
| N интер- | |||||||||||
| вала | 
| ||||||||||
| Гранииы ин- | |||||||||||
| тервала Ij | |||||||||||
| Число mj | |||||||||||
| наблюдений |
| Частота mj/n | 0.035 | 0.055 | 0.075 | 0.120 | 0.245 | 0.205 | 0.130 | 0.085 | 0.035 | 0.015 |
На рисунках 5,6 представлены три выборочные распределения. В
частности, на рис.5 в точке х=115 высота кумулятивной кривой W(х) равна 0.035+0.055+0.075=0.165, в точке х=140 W(х)=0.95, а W(150) = 1 .
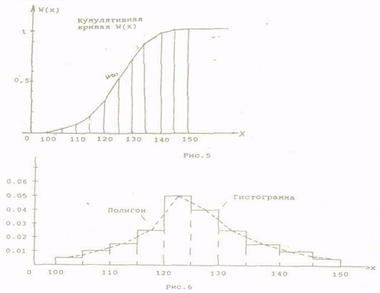 |
Высота гистограммы в точке х=117 (рис.6) равна m4/nl = 0.120/5 = 0.024.
Дата добавления: 2016-02-27; просмотров: 1148;
