ИНТЕРВАЛЬНЫЕ ОЦЕНКИ
Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.
1. Интервальной оценкой с надежностью 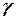 математического ожидания а нормально распределенного количественного признака по выборочной средней
математического ожидания а нормально распределенного количественного признака по выборочной средней 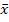 при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
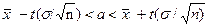 ,
,
Где 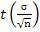 =δ – точность оценки, n - объем выборки, t – значение аргумента функции Лапласа Ф(t) при котором Ф(t)=γ/2.
=δ – точность оценки, n - объем выборки, t – значение аргумента функции Лапласа Ф(t) при котором Ф(t)=γ/2.
2. При неизвестном σ (и объеме выборки n<30)
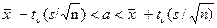 ,
,
где s - «исправленное» выборочное среднее квадратическое отклонение, t находят по таблице квантилей распределения Стьюдента по заданным n и γ.
Пример 1. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания a нормально распределенного признака X генеральной совокупности, если генеральное среднее квадратичное отклонение σ = 5, выборочная средняя 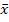 = 14 и объем выборки n = 25.
= 14 и объем выборки n = 25.
Решение. Требуется найти доверительный интервал
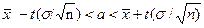 ,
,
Все величины, кроме t, известны. Найдем t из соотношения Ф(t) = 0,95/2=0,475. По таблице находим t = 1,96. Подставив t = 1,96, 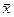 = 14, σ = 5, n = 25, окончательно получим искомый доверительный интервал 12,04 < a < 15,96.
= 14, σ = 5, n = 25, окончательно получим искомый доверительный интервал 12,04 < a < 15,96.
Пример 2. Из генеральной совокупности извлечена выборка объема n = 10, представленная в табл. 12.
Таблица 12
| варианта xi | -2 | |||||
| частота ni |
Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
Решение. Выборочную среднюю и «исправленное» среднее квадратичное отклонение найдем соответственно по формулам:
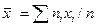 ,
, 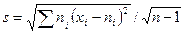 .
.
Подставив в эти формулы данные задачи, получим 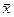 = 2, s = 2,4. Найдем tγ. Пользуясь таблицей, по γ = 0,95 и n = 10 находим tγ = 2,26. Найдем искомый доверительный интервал:
= 2, s = 2,4. Найдем tγ. Пользуясь таблицей, по γ = 0,95 и n = 10 находим tγ = 2,26. Найдем искомый доверительный интервал:
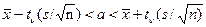 .
.
Подставляя в эти формулы данные задачи, получим 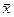 = 2, tγ = 2,26, s = 2,4, n= 10, получим искомый доверительный интервал 0,3< a < 3,7, покрывающий неизвестное математическое ожидание а с надежностью 0,95.
= 2, tγ = 2,26, s = 2,4, n= 10, получим искомый доверительный интервал 0,3< a < 3,7, покрывающий неизвестное математическое ожидание а с надежностью 0,95.
3. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания a нормально распределенного признака X генеральной совокупности, если известны генеральное среднее квадратичное отклонение σ, выборочная средняя 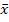 и объем выборки n: a) σ = 4,
и объем выборки n: a) σ = 4, 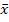 = 10,2, n=16; б) σ = 5,
= 10,2, n=16; б) σ = 5, 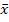 = 16,8, n = 25.
= 16,8, n = 25.
4. Одним и тем же прибором со средним квадратическим отклонением случайный ошибок измерений σ = 40 м произведено пять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния а до цели с надежностью γ = 0,95, зная среднее арифметическое результатов измерений 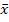 = 2000 м. Предполагается, что результаты измерений распределены нормально.
= 2000 м. Предполагается, что результаты измерений распределены нормально.
5. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности а горения лампы всей партии, если известно, что среднее квадратичное отклонение продолжительности горения лампы σ = 40 ч. Предполагается, что продолжительность горения ламп распределена нормально.
6. Из генеральной совокупности извлечена выборка объема n = 12, представленная в табл. 13. Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
Таблица 13
| варианта xi | -0,5 | -0,4 | -0.2 | 0,2 | 0,6 | 0,8 | 1,2 | 1,5 | ||
| частота ni |
Дата добавления: 2016-03-15; просмотров: 4478;
