СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОГО

СЛУЧАЙНОГО ВЕКТОРА

Пример1. Вычислить выборочные средние 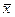, , 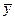несмещенные оценки дисперсий 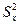, 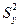и коэффициент корреляции для выборки

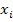
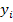
Решение. Для расчетов воспользуемся формулами

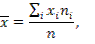
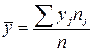, (4)

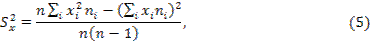
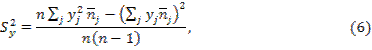
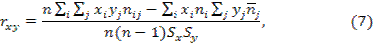
где n – объем выборки, n_ij– частота появления пары элементов (x_i, y_j) выборки; n_i – частота появления элемента x_i (при любом y); n_j – частота появления элемента y (при любом x).

В рассматриваемом примере среди значений x_i, y_j нет повторяющихся, поэтому

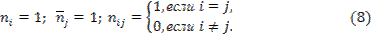
Вычисления удобно свести в таблицу.

Таблица 8

i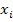

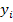
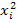
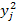
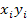
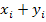
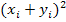
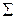
Последний столбец таблицы служит для контроля вычислений с помощью тождества

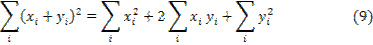
(В данном случае: 530 = 334 + 2∙86 + 24).

Используя данные из последней строки и учитывая (8),по формулам (4)–(7)получаем

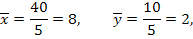
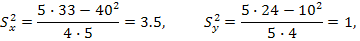
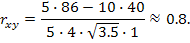
Пример 2.В табл. 9приведены результаты измерений двух физических величин в ходе некоторого эксперимента

Таблица 9

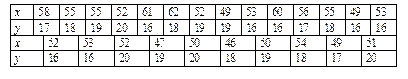
Вычислить средние, несмещенные оценки дисперсий и коэффициента корреляции, предварительно сгруппировав выборку и составив корреляционную таблицу.

Решение. Определим размах выборки по хи по у

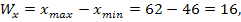
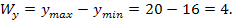
В данном случае для группировки элементов выборки удобно использовать четыре интервала по хи два интервала по у.Определим длины интервалов группировки

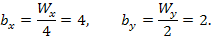
Группировку выборки можно производить по диаграмме рассеивания (см. рис. 9). Для построения этой диаграммы нанесем элементы выборки (x_i, y_j) в виде точек на плоскость с выбранной системой координат.

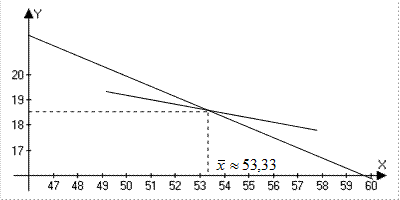
Рис. 9

Будем считать, что элементы выборки, которые попали на границу двух соседних прямоугольников, относятся к верхнему или к правому прямоугольнику, и составим корреляционную таблицу.

Таблица 10

y	x	46-50	50-54	54-58	58-62
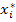
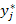
16-18
18-20

Здесь x_i^*, y_j^* – означают середины интервалов группировки. В клетках таблицы записываются частоты (то есть число пар исходной выборки, попавших в данный прямоугольник) для каждого прямоугольника на диаграмме рассеивания.

Для вычисления искомых оценок параметров распределения по сгруппированной выборке можно использовать те же формулы (4)–(7),в которых x_i, y_jследует заменить на x_i^*, y_j^*, а 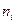, , 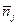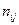– на частоты попадания элементов выборки в соответствующие интервалы , , .

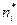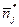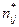Однако, если x_i^*, y_j^*достаточно велики, то для упрощения вычислений рекомендуется ввести вспомогательные случайные величины

где d_x, d_y–наиболее часто встречающиеся значения x_i^* и y_j^*.Найти их параметры распределения по формулам, аналогичным (4)–(7),а затем воспользоваться соотношениями

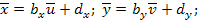(11)

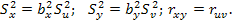
В заданном примере .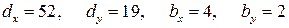

Результаты промежуточных вычислений представим в виде таблицы (табл. 11).

По формулам (4) - (7)используя найденные в таблице вспомогательные суммы 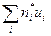, , 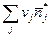, , 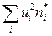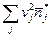и вычислив 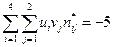имеем

Таблица 11

xi*
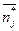
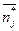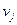
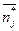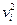
yj*	ui vj	-1
	-1						-10
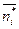
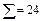
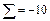
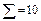
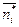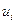
	-5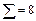

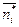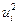
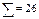
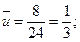
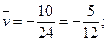
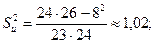
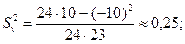
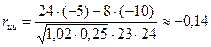
Возвращаясь к заданным случайным величинам, по формулам (11) получим

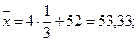
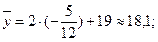
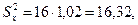
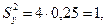
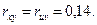
Пример 3. По выборке из примера 2 оценить параметры линейной регрессии X на Y и Y на X и составить уравнения прямых регрессии.

Решение. Уравнения прямых регрессии Y на X и X на Y были получены в курсе теории вероятностей и имеют вид

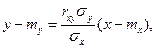
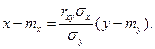
Заменяя в этих уравнениях числовые характеристики m_x, m_y, 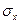, , 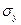r_xy их статистическими оценками, получим

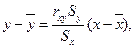(12)

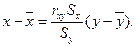(13)

Подставляя в эти уравнения найденные в предыдущем примере значения 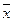, , 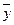S_x, S_y, r_xy имеем

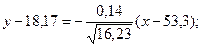
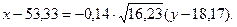
Отсюда следует, что уравнения линейной регрессии Y на X и X на Y имеют соответственно вид

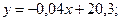
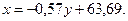
Отметим, что эти прямые пересекаются в точке ( 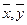). Угол между ними уменьшается при увеличении 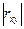, а при 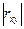= 1, прямые регрессии совпадают.

Решите примеры, используя данные своего варианта, приведенные в Приложении 2, табл. 1,2.

4. В ходе некоторого эксперимента были многократно измерены две физические величины X и Y. Результаты измерений записаны в таблицу. Обработайте результаты эксперимента по следующему плану:

1) постройте диаграмму рассеивания;

2) составьте корреляционную таблицу;

3) вычислите средние, несмещенные оценки дисперсий среднеквадратичных отклонений и оцените коэффициент корреляции;

4) составьте уравнения прямых регрессии и нанесите эти прямые на диаграмму рассеивания.

5. Вычислить выборочные средние 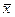, , 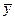несмещенные оценки дисперсий 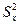, 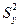и коэффициент корреляции для выборки, представленной в табл. 2 приложения 2.