Метод наименьших квадратов.
1.Корелляционные зависимости. Две основные задачи теории корреляции.
Во многих задачах требуется установить и оценить зависимость изучаемой величины Y от одной или нескольких величин. Рассмотрим сначала зависимость Y от одной СВ Х.
Строгая функциональная зависимость реализуется редко, т.к. обе величины или одна из них подвержена еще действию случайных факторов. В этом случае возникает статистическая зависимость.
Статистической называют зависимость, при которой изменения одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.
Условным среднем 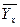 называют среднее арифметическое значение Y соответствующих значению X=x.
называют среднее арифметическое значение Y соответствующих значению X=x.
Корреляционной зависимостью Y от X называют функциональную зависимость условной средней 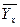 от x
от x 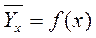 .
.
Уравнение называют уравнением регрессии, функцию f(x) называют регрессией Y на X, а ее график линией регрессии Y на X. Аналогично и 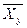 , X на Y .
, X на Y .
Первая задача теории корреляции – установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратичная, показательная и т.д.).
Вторая задача теории корреляции – оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости Y от X оценивается по величине рассеяния значений Y вокруг условного среднего 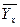 .
.
Дата добавления: 2016-03-05; просмотров: 617;
