Линейная корреляция.

Допустим, что количественные признаки X и Y связаны линейной корреляционной зависимостью. В этом случае обе линии регрессии будут прямыми.

Предположим, что для отыскания уравнений этих прямых проведено n пар чисел (x₁ y₁),(x₂ y₂)….(x_ny_n).

Поскольку наблюдаемые пары чисел можно рассматривать как случайную выборку из непараллельной совокупности всех возможных значений СВ (X,Y), то величины и уравнения, найденные по этим данным, называют выборочными. Если корреляция линейна имеем:

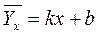или

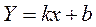
k-выборочный коэффициент регрессии ,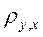

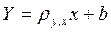
Подберем параметры 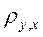и b так, чтобы сумма квадратов отклонений была минимальна.

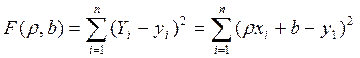
Для отыскания минимума продифференцируем

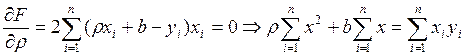
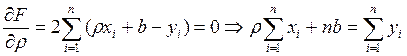
Решив эту систему, найдем:

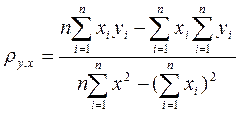
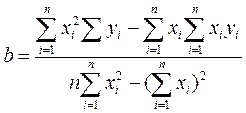
Свойство 1. Абсолютная величина выборочного коэффициента корелляции не превосходит 1.

Любая дисперсия не отрицательна.

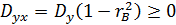Þ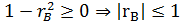

Свойство 2. Если выборочный коэффициент корреляции равен 0,то X и Y не связаны линейной корреляционной зависимостью:при

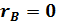Þ 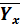-Y=0 Þ 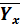=Y,аналогично 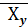=Xт.о. условные средние сохраняют постоянные значения при соответствующих изменениям аргумента.

Свойство 3. Если абсолютная величина выборочного коэффициента корреляции равна 1, то наблюдаемые значения признаков связаны линейной функциональной зависимостью:

.

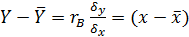Свойство 4. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 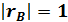переходит в функциональную.