Линейная дискриминантная функция Фишера
7.4 Дискриминация с использованием решающего правила, основанного на межвы-борочной вариации некоторого признака, будет тем более надежной, чем меньшими ве-роятностями совершить ошибки e1 и e2 это правило будет сопровождаться. Согласно формулам (7.4) и (7.5) эти вероятности уменьшаются, если значения t1 и t2 увеличивают-ся. В свою очередь, величины ti будут тем больше, чем больше будет разность ½M1 - M2½ по отношению к дисперсиям s12 и s22. Таким образом, признак будет обеспечивать тем лучшую дискриминацию, чем больше по нему будет межгрупповая изменчивость относи-тельно изменчивости внутригрупповой, и следовательно, чем больше будет отношение
- 169 -

Рисунок 7.2 Определение линейной дискриминантной функции Y на основе двух исходных признаков X1 и X2
(Величина межгрупповой изменчивости)
 L = . (7.12)
L = . (7.12)
(Величина внутригрупповой изменчивости)
Обычно в наборе рассматриваемых исходных признаков отсутствуют такие, у любо-го из которых решающее правило обеспечивает приемлемые вероятности ошибок дискри-минации. Вместе с тем, можно попытаться на базе исходного набора m признаков X, в который входят X1, X2, X3, ..., Xm, найти некоторую новую переменную, для которой от-ношение L, найденное по формуле (7.12), достигало бы максимального уровня L = max. Тогда решаеющее дискриминантное правило, построенное на его основе, обеспечит ми-нимально возможные для данной ситуации вероятности ошибок e1 и e2. Так, может встретиться ситуация, изображенная на рисунке 7.2. Здесь два распределения для каждого из двух исходных признаков обнаруживают заметную межгрупповую трансгрессию, что будет сопровождаться значительными вероятностями ошибок дискриминации для одномерных решающих правил, построенных на их основе. Очевидно, что ни одно из них не сможет эффективно работать для дискриминации случайно взятых индивидов. Однако, если провести ось нового признака Y так, как это показано на рисунке 7.2, два распределения этого признака обнаружат практическое отсутствие межгрупповой
- 170 -
Рисунок 7.3 Распределение значений линейной дискриминантной функции Фишера
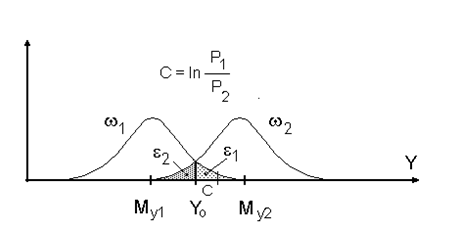 |
трансгрессии и хорошую работоспособность построенного на основе Y решающего правила.
7.5 Новый признак Y, обладающий наилучшими возможностями дискриминации, может быть получен как линейная комбинация
Y = b'X = b1X1 + b2X2 + b3X3 + ... + bmXm . (7.13)
Вектор b, определяющий свойства нового признака Y, должен быть таким, чтобы отношение L (7.12) достигало бы максимального значения. Величина межгрупповой вариации для него может быть определена квадратом разности двух его средних величин
(My2 - My1)2 = (b'M2- b'M1)2 = [b'(M2 - M1)]2,
где M2 и M1 - векторы средних набора исходных признаков в двух группах населения w1 и w2. Внутригрупповая вариация признака Y может быть измерена его дисперсией sy2. Пусть ковариационные матрицы исходного набора признаков S1 и S2 в двух группах населения различаются мало, и по ним можно получить единую оценку
N1S1 + N2S2
 S = .
S = .
N1 + N2
Дата добавления: 2016-02-13; просмотров: 1656;
