Криволинейная корреляция
 – параболическая корреляция.
– параболическая корреляция.
Нужно получить уравнение регрессии
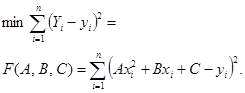
Находим производные
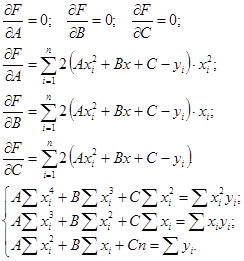
пример.
| Y | X | ny | |||
| – 2 | |||||
| – 1 | |||||
| nx |
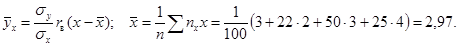
Критерий согласия
Если можно прогнозировать законы распределения некоторой случайной величины, то параметры закона распределения находят методом моментов. Этот метод заключается в приравнивании параметров теоретического распределения к выборочным оценкам этих параметров.
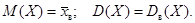
пример. Известно, что X распределена по показательному закону. Заданы выборочные значения этой случайной величины.
| xi | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 | 27,5 |
| ni |
Найти закон распределения.
Решение
Показательное распределение имеет вид:

Пусть случайная величина X распределена по некоторому неизвестному закону F0(x).
Определение. Статистическая гипотеза – это любое предположение о законе распределения случайной величины X или о его параметрах.
Выдвинутая гипотеза называется нулевой.
H0: X распределена по F0(x)
Противоположная ей гипотеза называется конкурирующей, или альтернативной.
H1: X не распределена по F0(x)
Гипотеза называется простой, если она однозначно определяет закон распределения, иначе она называется сложной.
пример. 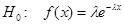
Пусть λ = 5 – простая гипотеза.
Пусть λ ≤ 5 – сложная гипотеза.
Для проверки гипотезы формируется статистический критерий, который однозначно определяет выборки, для которых гипотеза отвергается, и выборки для которых гипотеза принимается. Множество выборок, для которых H0 принимается, обозначим G, называется областью допустимых значений или иногда областью применимости гипотезы, а множество выборок, для которых гипотеза отвергается, обозначим W, называется критической областью.
По каждой выборке просчитывается наблюдаемое значение критерия Kнабл, которая сравнивается с известным значением этого критерия Ккр (табличное значение).
Критическая область W может быть правосторонней, левосторонней и двусторонней.
 1) правосторонняя критическая область W.
1) правосторонняя критическая область W.
 2) левосторонняя критическая область W.
2) левосторонняя критическая область W.
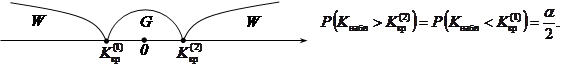 3) двусторонняя критическая область W.
3) двусторонняя критическая область W.
При обработке гипотезы возможны 4 варианта.
1) H0 верна и принимается на основании K.
2) H0 неверна и отвергается на основании K.
3) H0 верна и отвергается на основании K, т.е. происходит ошибка первого рода.
Вероятность ошибки первого рода α называется уровнем значимости критерия.
α достаточно мало и задается наперед.
4) H0 неверна и принимается на основании K, т.е. происходит ошибка второго рода, обозначим ее вероятность β.
Очевидно, чем меньше α, тем больше вероятность принять гипотезу, т.е. тем больше β.
Мощностью критерия называется число 1 – β. Если β – это вероятность совершить ошибку второго рода, то мощность – это вероятность не совершить ошибку второго рода.
Критерии, по которым определяется закон распределения случайной величины называются критериями согласия.
Критерия Пуассона
H0: X распределена по F0(x). Пусть задана некоторая выборка.
| xi | x1 | ....... | xk |
| ni | n1 | ....... | nk |

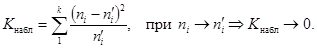
Критическая область правосторонняя.
1) Kнабл по выборке.
2) Kкр по таблице.
Kкр (α, k), k = s – r – 1 – количество степеней свободы системы.
где s – число классов в выборке;
r – число параметров распределения.
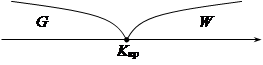 3)
3)
Кнабл > Ккр Þ H0 отвергается.
Кнабл < Ккр Þ H0 принимается.
Если статистический ряд распределения дискретен, то 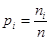 ,
,
а если ряд непрерывен, то 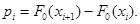
пример. При уровне значимости α = 0,025 нужно проверить гипотезу о нормальном распределении X.
| (4; 6) | (6; 8) | (8; 10) | (10; 12) | (12; 14) | (14; 16) | (16; 18) | (18; 20) | (20; 22) | |

| xi | xi+1 | 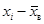
| 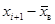
| 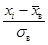
| 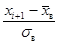
| 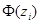
| 
| pi | 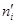
| 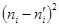
| 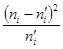
| ni |
| – | – 6,63 | – ∞ | – 1,41 | – 0,5 | – 0,4207 | 0,0793 | 15,86 | 0,7396 | 0,0466 | |||
| – 6,63 | – 4,63 | – 1,41 | – 0,99 | – 0,4207 | – 0,3389 | 0,0818 | 16,36 | 92,9296 | 5,6803 | |||
| – 4,63 | – 2,63 | – 0,99 | – 0,156 | – 0,3389 | – 0,2123 | 0,1266 | 25,32 | 0,1024 | 0,0040 | |||
| – 2,63 | – 0,63 | – 0,156 | – 0,13 | – 0,2123 | – 0,0517 | 0,1606 | 32,12 | 4,4944 | 0,1399 | |||
| – 0,63 | 1,37 | – 0,13 | 0,29 | – 0,0517 | 0,1141 | 0,1658 | 33,16 | 51,2656 | 1,5460 | |||
| 1,37 | 3,37 | 0,29 | 0,72 | 0,1141 | 0,2642 | 0,1501 | 30,02 | 81,3604 | 2,7102 | |||
| 3,37 | 5,37 | 0,72 | 1,14 | 0,2642 | 0,3729 | 0,1087 | 21,74 | 5,1076 | 0,2349 | |||
| 5,37 | 7,37 | 1,14 | 1,57 | 0,3729 | 0,4418 | 0,0689 | 13,78 | 38,6884 | 2,8076 | |||
| 7,37 | – | 1,57 | ∞ | 0,4418 | 0,5 | 0,0582 | 11,64 | 1,8496 | 0,1589 | |||
| å | из табл. | из табл. | 13,3284 |
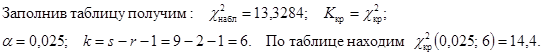
Вывод: 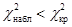 Þ H0 принимается; следовательно случайная величина X распределена нормально.
Þ H0 принимается; следовательно случайная величина X распределена нормально.
Дата добавления: 2016-02-27; просмотров: 2125;
