Точечная оценка параметров распределения
θ – параметр генеральной совокупности;
θв – выборочное значение;
θв – оценка θ.
Если оценка задается одним числом, то она называется точечной.
Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.
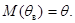
Оценка называется эффективной, если она имеет наименьшую из возможных дисперсий.
Оценка называется состоятельной, если она стремится по вероятности к оцениваемому параметру.
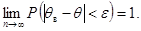
1. Выборочная средняя
Утверждение. 
– несмещенная состоятельная оценка M(X). Если генеральная совокупность распределена по нормальному закону, то оценка является эффективной.
2. Выборочная дисперсия
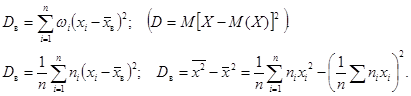
Выборочная дисперсия – смещенная оценка дисперсии генеральной совокупности.
S2 – несмещенная оценка D(X)
S2 – исправленная выборочная дисперсия.
при n > 30 S2 ≈ Dв
3. Выборочное среднее квадратическое отклонение
Условные варианты
| xi | x1 | ....... | xk |
| ni | n1 | ....... | nk |
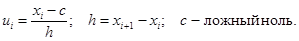
Утверждение. 
Доказательство
пример.
Вычислить выборочные характеристики случайной величины X, заданной рядом.
| xi | 10,2 | 10,4 | 10,6 | 10,8 | 11,2 | 11,4 | 11,6 | 11,8 | |||
| ni | n = 100 |
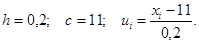
| xi | ni | ui | ui · ni | ui2 · ni | ni · (ui + 1)2 |
| 10,2 | – 4 | – 8 | |||
| 10,4 | – 3 | – 9 | |||
| 10,6 | – 2 | – 16 | |||
| 10,8 | – 1 | – 13 | |||
| 11,0 | S– = – 46 | ||||
| 11,2 | |||||
| 11,4 | |||||
| 11,6 | |||||
| 11,8 | |||||
| 12,0 | |||||
| S+ = 103 | |||||
| ∑ |
Контроль
Интервальная оценка параметров распределения
Интервальной называется оценка, если задается двумя числами – концами интервалов.
Пусть θв – выборочная оценка некоторого параметра θ генеральной совокупности.
Доверительной вероятностью или надежностью γ называется вероятность того, что оценка θв имеет точность δ.
Доверительным интервалом оценки θв называется интервал,
который показывает оцениваемый параметр θ с заданной надежностью γ.
Пусть случайная величина X распределена по нормальному закону с параметрами a и σ.
Интервальные оценки математического ожидания a.
1) σ известна:
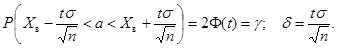
пример. Пусть 
Решение
2) σ неизвестна:
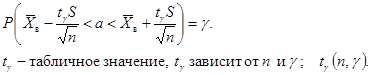
Интервальная оценка σ.
Элементы теории корреляции
X, Y – некоторые случайные величины.
Величины X и Y связаны статистической зависимостью, если при изменении значений одной из них меняется закон распределения другой. Если при этом меняется среднее значении величины, то зависимость называется корреляционной.
Mx(X) = f(x) – условное математическое ожидание случайной величины Y.
My(X) = φ(y) – условное математическое ожидание случайной величины X.
Это уравнения регрессии.
Выведем уравнение линейной регрессии.
Для нахождения k и b применим метод наименьших квадратов.
Пусть (xi; yi) – заданное значение по выборке, Yi – значение Y по (1).
Применим метод наименьших квадратов.
Он состоит в следующем – минимизируют сумму квадратов отклонения.
Аналогично
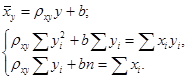
пример. Записать уравнение линейной регрессии для выборки
| x | 1,5 | 4,5 | ||||
| y | 1,25 | 1,4 | 1,5 | 1,75 | 2,25 | n=5 |
| xi | yi | xiyi |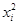 
| 
| |
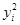
| 1,25 | 1,25 | 1,56 | |||
| 1,5 | 1,4 | 2,1 | 2,25 | 1,96 | |
| 1,5 | 4,5 | 2,25 | |||
| 4,5 | 1,75 | 7,88 | 20,25 | 3,06 | |
| 2,25 | 11,25 | 5,06 | |||
| ∑ | 8,15 | 26,975 | 57,5 | 13,89 |
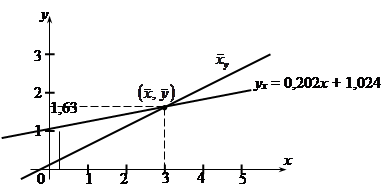
Пусть данные сгруппированы
каждое значение x встречается nx раз
каждое значение y встречается ny раз
(x; y) – nxy раз.
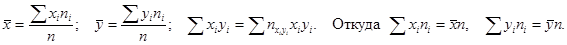
Проводим эту замену в системе для несгруппированных данных, получаем новую систему для нахождения в.
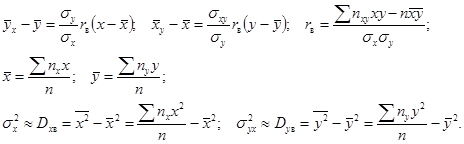
rв – называется коэффициентом корреляции характеризует тесноту связи между случайными величинами x и y.
Если rв = 0 Þ X, Y независимы.
Если rв = ± 1 Þ функциональная зависимость
– 1 < rв < 1 чем ближе к |1|, тем сильнее зависимость.
Дата добавления: 2016-02-27; просмотров: 1032;