МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Совокупность всех рассматриваемых объектов называется генеральной совокупностью.
Выборной или выборочной совокупностью называется совокупность отобранных из генеральной совокупности объектов.
Количество объектов выборки называется ее объемом. Задача математической статистики заключается в том, чтобы обосновать свойства генеральной совокупности на основании свойств выборки.
Выборка должна быть репрезентативной, т.е. каждый объект выборки должен быть отобран случайно и все объекты имеют одинаковую вероятность попасть в выборку.
Элементы выборки x1, x2, ... , xn – отличные друг от друга называются вариантами. Варианты, расположенные в порядке возрастания называются вариационным рядом.
Число появлений xi в выборке называется частотой ni.
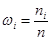 – относительная частота варианты xi.
– относительная частота варианты xi.
Статистический ряд распределения частот.
| xi | x1 | x2 | ....... | xk | 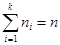
|
| ni | n1 | n2 | ....... | nk |
Статистический ряд распределения относительных частот.
| xi | ....... | 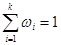
|
| ωi | ....... |
Для непрерывной случайной величины составляют интервальный ряд
| (x1; x2) | (x2; x3) | ....... | (xk-1; xk) | |
| ni или ωi | n1 | n2 | ....... | nk |
(xi; xi+1) – классы
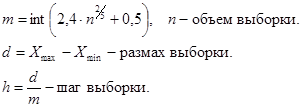
Эмпирическая функция распределения
Обозначим nx – частота появления значений X < x
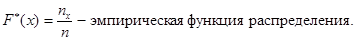
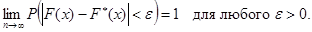
F*(x) – эмпирическая функция распределения.
Свойства F*(x)
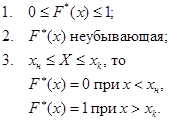
пример. Был измерен рост выбранных людей (32 человека) с точностью до 0,1. Найти F*(x).
| 181,3; | 183,4; | 175,0; | 174,4; |
| 171,3; | 184,6; | 164,8; | 176,1; |
| 177,3; | 167,2; | 168,9; | 166,2; |
| 180,9; | 170,9; | 173,6; | 170,1; |
| 173,4; | 171,6; | 188,8; | 176,8; |
| 170,7; | 175,6; | 167,2; | 176,8; |
| 176,1; | 176,8; | 170,6; | 173,3; |
| 170,3; | 182,7; | 175,4; | 167,7 |
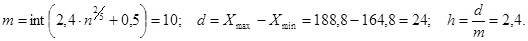
| (xi, xi+1) | ni | 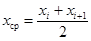
| 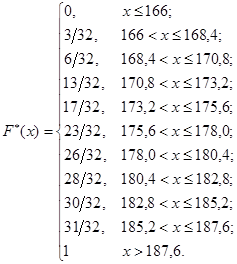
|
| 164,8 – 167,2 | |||
| 167,2 – 169,6 | 168,4 | ||
| 169,6 – 172 | 170,8 | ||
| 172 – 174,4 | 173,2 | ||
| 174,4 – 176,8 | 175,6 | ||
| 176,8 – 179,2 | 178,0 | ||
| 179,2 – 181,6 | 180,4 | ||
| 181,6 – 184,0 | 182,8 | ||
| 184,0 – 186,4 | 185,2 | ||
| 186,4 – 188,8 | 187,6 |
Если выборка записана дискретным случайным рядом, то графически он изображается полигоном распределения.
Полигон распределения
Полигон распределения – это ломаная, которая соединяет точки xi и ni.
Дата добавления: 2016-02-27; просмотров: 733;
