Математическая модель вулканизации ПЭ

Допущения:

· С_м/С_к»1, то можно продолжить расчет по нижеприведенной методике.

· Переходим к сплошному цилиндру

· Среда однородна изотропна

· На поверхности создается мономолекулярный слой

Что дает нам решать линейную задачу.

· Задача нестационарная

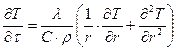
· Численная реализация:

Позволяет решить задачу по слоям (то есть С_м/С_к»1 → к сплошному цилиндру – Не учитываем ).

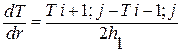
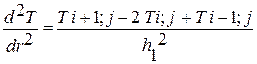
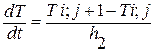
НУ: Тн = Т пэ. вых

ГУ:

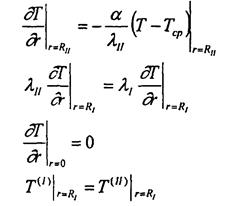
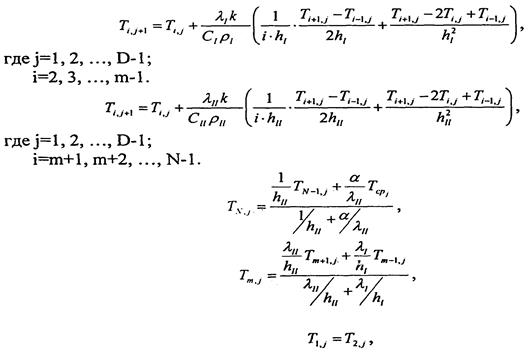
• Аналитическое решение:

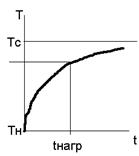
Рассчитать кривую нагрева внутреннего слоя первого экрана изоляции.

,

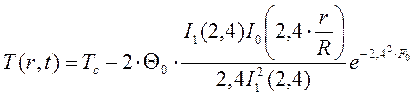где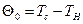

Т_с – температура среды, в которой протекает вулканизация (пар, инфракрасный нагрев, жидкость);

Т_н – температура изоляции, выходящей из головки; °С;

I_0, I₁ – функции Бесселя первого рода нулевого и первого порядка: ;

r – радиус ТПЖ, м;

R – внешний радиус изделия (по изоляции, по внешнему экрану), м;

F₀ – критерий Фурье ,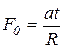

где 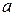- коэффициент температуро-проводности ПЭ. 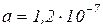м²/с; (в интервале температур 140-200°С;

t – время, с; R – м.

Результат двух случаев:

Изоляция считается прогретой если Т-ра на поверхности 15-20 градусов ниже температуры среды.

Изоляция считается прогретой ,когда 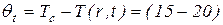°С.

Время нагрева можно определить по графику или рассчитать по формуле

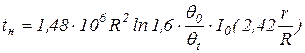, [c] - Справедлива для однослойного цилиндра

Рассчитать время полураспада дикумила

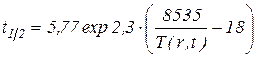, [с]

где Т – температура внутреннего слоя первого экрана (изоляции) в конце нагрева, К. Т=Т_с-(15-20)+273

Рассчитать время вулканизации .

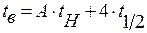
где А – коэффициент, учитывающий наличие процесса вулканизации во внутренних слоях изоляции при охлаждении до 145°С. А – зависит от толщины изоляции.

Рассчитать скорость вулканизации

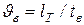
Рассчитать необходимое давление охлаждающей среды (газ, жидкость), которое необходимо для получения беспористой изоляции .

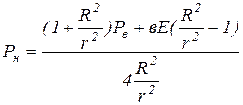
где 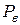- давление в головке пресс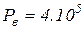а, Па;

Е – модуль упругости ПЭ в интервале температур 90-120°С, Е=7.10⁷ Па ;

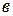- суммарная усадка изоляции в интервале температур 90-120°С (т.к. в этом диапазоне происходит основная усадка – фазовый переход), 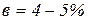(т.е. 0,04-0,05).