Для равноточных измерений.
Оценка математического ожидания случайной величины 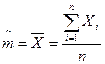 ; покажем, что эта оценка является состоятельной и несмещенной.
; покажем, что эта оценка является состоятельной и несмещенной.
Согласно закону больших чисел
 .
.
Это значит, что 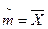 является состоятельной.
является состоятельной.
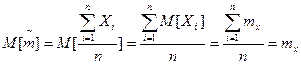 - условие несмещенности.
- условие несмещенности.
Оценка дисперсии.
Рассмотрим статистическую дисперсию 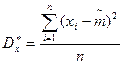 . Преобразуем
. Преобразуем
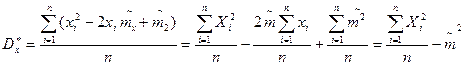
Первый член в правой части представляет собой среднее арифметическое n наблюдаемых значений СВ Х2 , следовательно он сходится по вероятности к M[X2]. Второй член 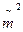 сходится по вероятности к
сходится по вероятности к 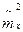 . Это значит, что вся правая часть сходится по вероятности к величине
. Это значит, что вся правая часть сходится по вероятности к величине 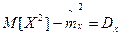 , следовательно статистическая дисперсия является состоятельной.
, следовательно статистическая дисперсия является состоятельной.
Проверим является ли она несмещенной, для этого вместо 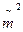 подставим его значение
подставим его значение
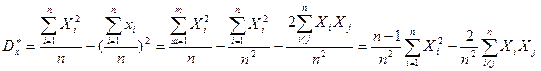 .
.
Так как дисперсия Dx не зависит от того, в какой точке выбрать начало координат, то выберем его в точке mx и найдем математическое ожидание M[Dx*]

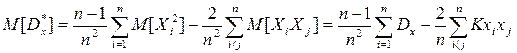 , т.к. опыт независим Kxixj=0Þ
, т.к. опыт независим Kxixj=0Þ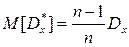 -не удовлетворяет условию несмещенности, но если Dx* умножить на
-не удовлетворяет условию несмещенности, но если Dx* умножить на 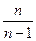 , она будет несмещенна, а т.к.
, она будет несмещенна, а т.к. 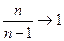 , при n®¥, то
, при n®¥, то 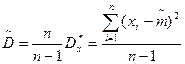 будет состоятельным.
будет состоятельным.
2)Для неравноточных измерений. 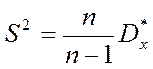
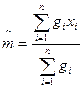 .где
.где 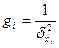 - вес измерения
- вес измерения
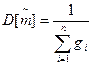
3)Для системы двух СВ X,Y 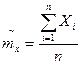
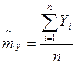
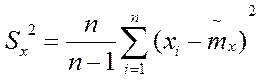 ;
; 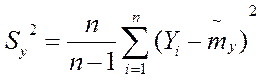
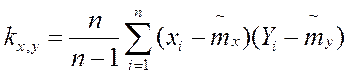
Дата добавления: 2016-03-05; просмотров: 715;
