Алгоритмы обработки многократных измерений.
Методика обработки результатов МНОГОКРАТНЫХ ПРЯМЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ.
Этапы:
1. исправляют результаты наблюдений исключением систематической погрешности;
2. вычисляют средне арифметическое значение 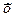 по формуле:
по формуле: 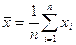 ;
;
3. вычисляют выборочное СКО от значения погрешности измерений по формуле: 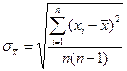 ;
;
4. исключают промахи;
5. определяют закон распределения случайной составляющей;
6. при заданном значении доверительной вероятности Р и числе измерений n по таблицам определяют коэффициент Стьюдента 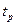 ;
;
7. находят границы доверительного интервала для случайной погрешности 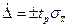 ;
;
8. если величина 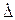 сравнима с абсолютным значением погрешности СИ, то величину
сравнима с абсолютным значением погрешности СИ, то величину 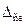 считают неисключенной систематической составляющей и в качестве доверительного интервала вычисляют величину
считают неисключенной систематической составляющей и в качестве доверительного интервала вычисляют величину 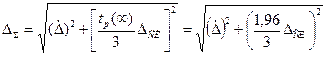
или по упрощенной формуле 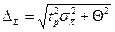 , где Θ границы неисключенной составляющей погрешности;
, где Θ границы неисключенной составляющей погрешности;
9. окончательный результат записывают в виде 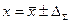 при вероятности Р.
при вероятности Р.
Методика обработка результатов косвенных измерений.
Косвенные измерения предполагают наличие функциональной связи Y=f(x1, x2, …xn), где х1, х2, …хn – подлежащие прямым измерениям аргументы функции Y.
Этапы:
1. для результатов прямых измерений аргументов хвычисляют выборочные средние 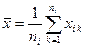 и выборочные стандартные отклонения
и выборочные стандартные отклонения 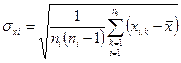 ;
;
2. для каждого аргумента вычисляют суммарные систематические погрешности в виде СКО: 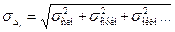 , где σсуб, σокр характеризуют разброс результатов из-за субъективных причин, округления и т.п.
, где σсуб, σокр характеризуют разброс результатов из-за субъективных причин, округления и т.п.
3. находят выборочное среднее функции по m аргументам с учетом коэффициента влияния 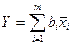 ;
;
4. вычисляют стандартные отклонения случайных и систематических составляющих функции 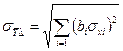 ,
, 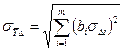 , где
, где 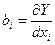 - абсолютный коэффициент влияния аргумента на функцию;
- абсолютный коэффициент влияния аргумента на функцию;
5. сравнивают 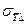 и
и 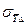 :
:
- если 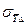 <<
<< 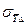 , то результат записывают в виде
, то результат записывают в виде 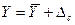 при вероятности Р. Здесь, задавшись вероятность Р, полуинтервал Δс находят с помощью коэффициентов Чебышева по формуле Δс=γр
при вероятности Р. Здесь, задавшись вероятность Р, полуинтервал Δс находят с помощью коэффициентов Чебышева по формуле Δс=γр 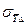 ;
;
- если 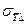 >>
>> 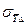 , то результат записывают как
, то результат записывают как 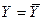 , при Р=α и
, при Р=α и 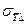
- если 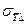 и
и 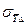 сравнимы, то результат представляют в виде
сравнимы, то результат представляют в виде 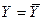 ;
; 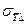 ;
; 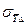 .
.
МЕТОДИКА ОПРЕДЕЛЕНИЯ И ИСКЛЮЧЕНИЯ ГРУБЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Установлены критерии для выявления промахов. Если априорно известна точность измерений через величину СКО (S), то при нормальном распределении экспериментальных данных предельно допустимые отклонения от среднего значения, составляют не более чем:
2/3 S с вероятностью не менее Р=0,5;
σ S вероятностью не менее Р=0,68;
2 S с вероятностью не менее Р=0,95;
2,6 S с вероятностью не менее Р=0,99;
3 S с вероятностью не менее Р=0,997.
Последнее правило является «правилом трёх сигм»: если при многократных измерениях одного и того же постоянного размера сомнительное значение результата измерений отличается от среднего значения больше, чем на 3σ , то его следует отбросить.
В большинстве случаев СКО не известно. Тогда промахи определяются по критериям:
· Романовского, при числе измерений n≤20. 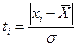 , где xi –проверяемое экспериментальное данное. Значение ti сравнивается с табличным tT. Если ti≥ tT, то проверяемое значение считается промахом.
, где xi –проверяемое экспериментальное данное. Значение ti сравнивается с табличным tT. Если ti≥ tT, то проверяемое значение считается промахом.
· Шарлье, при большом числе измерений 20<n<100. Промахом считаются результаты, для которых выполняется неравенство: 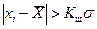 , где Кш значения критерия Шарлье (табличные).
, где Кш значения критерия Шарлье (табличные).
· Диксона, при небольшом числе экспериментальных данных: 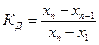 , где xn – проверяемое значение, х1 первое в ряду. Значение является промахом, если КД >zq , zq – табличное значение, для числа измерение n и заданного уровня значимости q.
, где xn – проверяемое значение, х1 первое в ряду. Значение является промахом, если КД >zq , zq – табличное значение, для числа измерение n и заданного уровня значимости q.
· Шовине, при n<10. Промахом считаются результаты, для которых выполняется неравенство: 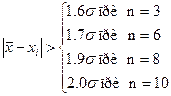
Дата добавления: 2016-04-22; просмотров: 1954;
