методов наименьших квадратов.

Метод наименьших квадратов применяется для решения различных задач, связанных с обработкой результатов опыта. Наиболее важным приложения этого метода является решение задачи сглаживания экспериментальной зависимости, т.е. изображение опытной функциональной зависимости аналитической формулой. Вид аналитической формулы определяется обработкой.

Пусть получено n экспериментальных точек с абсциссами x_1,x_2,..x_n и соответствующими ординатами y_1,y_2,..y_{n ,} но она не может совпадать с экспериментальными значениями y_i во всех n точках. Это означает, что для всех или некоторых точек разность 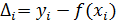будет отлична от нуля.

Требуется подобрать параметры функции f таким образом, чтобы сумма квадратов разностей 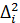было наименьшей, т.е.

.

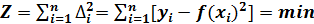При решении многих практических задач функциональную зависимость Y от X ищут в виде

.

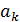- неизвестные параметры

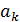-известные функции, т.е. нам необходимо подобрать , при которой функция

²=min.

Найдем частные производные и приравняем их к 0.

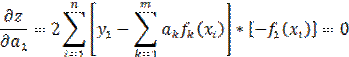
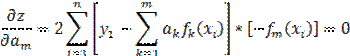
Подставляя в систему опытные значения X_i и Y_i мы получим систему m линейных уравнений относительно неизвестных параметров 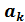, решение которой не представляет сложности.