В статике с помощью метода наименьших квадратов
Идентификация характеристик объектов энергетики
Идентификация параметров объектов энергетики проводится для построения их математических моделей с целью проведения научных исследований.
Идентификация в статике осуществляется в условиях установившегося режима, то есть по завершении переходных процессов.
Метод наименьших квадратов удобно использовать для объектов, статические характеристики которых описываются линейными зависимостями:
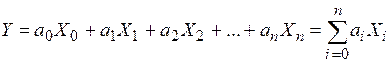 , (1.1)
, (1.1)
где: 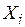 - входные величины;
- входные величины; 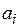 - параметры математической модели;
- параметры математической модели; 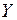 - выходная величина.
- выходная величина.
Величины 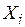 и
и 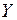 могут быть как электрическими, так и неэлектрическими.
могут быть как электрическими, так и неэлектрическими.
В процессе исследований проводят ряд экспериментов и измеряют величины 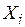 и
и 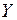 . Затем рассматривают погрешность (ошибку):
. Затем рассматривают погрешность (ошибку):
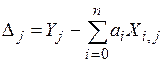 , (1.2)
, (1.2)
где:  - номер эксперимента;
- номер эксперимента; 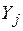 - экспериментальные значения выходной величины;
- экспериментальные значения выходной величины;  - экспериментальные значения входных величин.
- экспериментальные значения входных величин.
После этого записывают выражение для суммы квадратов погрешностей:
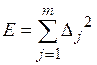 , (1.3)
, (1.3)
где: 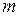 - количество экспериментов.
- количество экспериментов.
Затем составляют систему уравнений на основе выражений для частных производных:
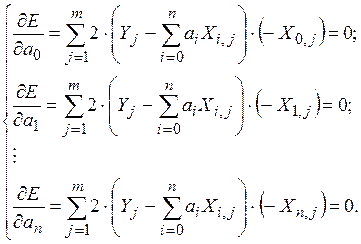 . (1.4)
. (1.4)
Разделив все уравнения на 2, и раскрывая скобки, получим:
 (1.5)
(1.5)
Решая эту систему, находят неизвестные параметры 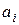 .
.
Задача 1
В результате эксперимента в установившемся режиме измерены значения суммарного тока нагрузки 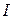 силового трансформатора, температуры окружающего воздуха
силового трансформатора, температуры окружающего воздуха 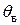 и температуры масла
и температуры масла 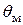 этого трансформатора (табл. 1.1).
этого трансформатора (табл. 1.1).
Таблица 1.1 – Результаты экспериментов
| Номер эксперимента | |||
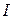 , А , А
| |||
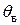 , ºС , ºС
| |||
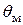 , ºС , ºС
|
Методом наименьших квадратов найти параметры математической модели:
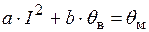 .
.
Решение
Необходимо найти неизвестные параметры 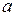 и
и 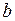 .
.
Составляем систему уравнений в соответствии с (1.5):
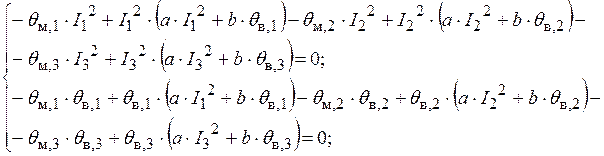
Подставив цифры из таблицы 1.1, и приведя подобные, получим:
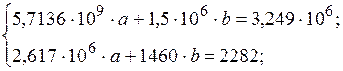
Решая систему, находим:
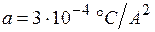 ;
; 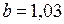 .
.
Задача 2
В результате эксперимента в установившемся режиме измерены значения частоты вращения 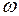 ротора турбогенератора, активной мощности
ротора турбогенератора, активной мощности 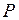 , генерируемой в сеть, выдаваемого напряжения
, генерируемой в сеть, выдаваемого напряжения  и максимальной амплитуды вибрации
и максимальной амплитуды вибрации 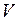 его корпуса (табл. 1.2).
его корпуса (табл. 1.2).
Таблица 1.2 – Результаты экспериментов
| Номер варианта | |||||||||
| Номер эксперимента | |||||||||
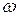 , об/мин , об/мин
| |||||||||
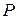 , МВт , МВт
| |||||||||
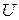 , кВ , кВ
| 9,8 | 10,4 | 9,7 | 9,9 | 10,4 | 9,5 | 9,7 | 10,1 | |
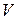 , мм , мм
| 0,235 | 0,168 | 0,093 | 0,364 | 0,226 | 0,07 | 0,448 | 0,292 | 0,054 |
Таблица 1.2 – продолжение
| Номер варианта | |||||||||
| Номер эксперимента | |||||||||
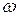 , об/мин , об/мин
| |||||||||
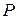 , МВт , МВт
| |||||||||
 , кВ , кВ
| 9,7 | 10,4 | 9,5 | 9,7 | 10,3 | 10,5 | 10,9 | ||
 , мм , мм
| 0,359 | 0,277 | 0,133 | 0,392 | 0,204 | 0,09 | 0,205 | 0,148 | 0,123 |
Методом наименьших квадратов найти параметры математической модели:
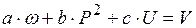 .
.
Определить размерности этих параметров.
| <== предыдущая лекция | | | следующая лекция ==> |
| Проверка гипотезы о корреляции случайных величин | | | в статике с помощью полного факторного эксперимента |
Дата добавления: 2016-02-16; просмотров: 539;
