Оконное преобразование Фурье

Частичным выходом из этой ситуации является оконное преобразование

Фурье с движущейся по сигналу оконной функцией, имеющей компактный носитель. Временной интервал сигнала разделяется на подинтервалы и преобразование выполняется последовательно для каждого подинтервала в отдельности. Тем самым осуществляется переход к частотно-временному (частотно-координатному) представлению сигналов, при этом в пределах каждого подинтервала сигнал "считается" стационарным. Результатом оконного преобразования является семейство спектров, которым отображается изменение спектра сигнала по интервалам сдвига окна преобразования. Это позволяет выделять на координатной оси и анализировать особенности нестационарных сигналов. Размер носителя оконной функции w(t) обычно устанавливается соизмеримым с интервалом стационарности сигнала. По существу, таким преобразованием один нелокализованный базис разбивается на определенное количество базисов, локализованных в пределах функции w(t), что позволяет представлять результат преобразования в виде функции двух переменных - частоты и временного положения окна.

Оконное преобразование выполняется в соответствии с выражением:

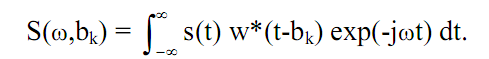(3.7)

Функция w*(t-b) представляет собой функцию окна сдвига преобразования по

координате t, где параметром b задаются фиксированные значения сдвига. При сдвиге окон с равномерным шагом значения bk принимаются равными 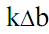. В качестве окна преобразования может использоваться как простейшее прямоугольное окно, так и специальные весовые окна (Бартлетта, Гаусса, и пр.), обеспечивающие малые искажения спектра при вырезке оконных отрезков сигналов (нейтрализация явления Гиббса).

Пример оконного преобразования для нестационарного сигнала на большом

уровне шума приведен на рис. 3.2. По спектру сигнала можно судить о наличии в

его составе гармонических колебаний на трех частотах, определять соотношение между амплитудами этих колебаний и конкретизировать локальность колебаний по интервалу сигнала.

Координатная разрешающая способность оконного преобразования определяется шириной оконной функции и обратно пропорциональна частотной разрешающей способности. При ширине оконной функции, равной b, частотная разрешающая

способность определяется значением 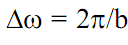. При требуемой величине частотного разрешения 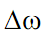соответственно ширина оконной функции должна быть равна 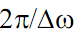. Для оконного преобразования Фурье эти ограничения являются принципиальными. Так, для рис. 3.2 при размере массива данных N = 300 и ширине оконной функции 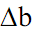= 100 частотная разрешающая способность результатов преобразования уменьшается в N/ 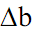= 3 раза по сравнению с исходными данными, и графики 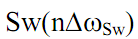по координате n для наглядного сопоставления с графиком 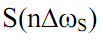по-

строены с шагом по частоте 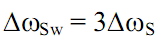, т.е. по точкам n = 0, 3, 6, … , N.

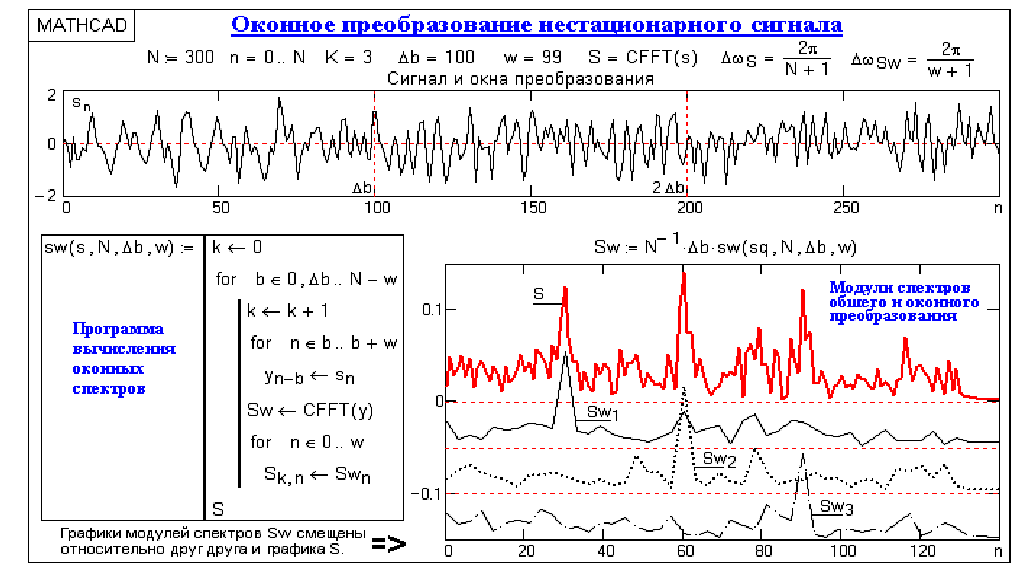
Рисунок 3.2 – Пример оконного преобразования

Частотно-временное оконное преобразование применяется для анализа не-

стационарных сигналов, если их частотный состав изменяется во времени. Функция оконного преобразования (3.7) может быть переведена в двухмерный вариант с независимыми переменными и по времени, и по частоте:

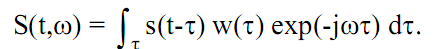(3.8)

На рис. 3.3 приведен пример вычисления и представления (модуль правой

части главного диапазона спектра) частотно-временной спектрограммы при дискретном задании входного сигнала sq(n). Сигнал представляет собой сумму трех последовательных радиоимпульсов с разными частотами без пауз, с отношением сигнал/шум, близким к 1. Оконная функция wi задана с эффективной шириной окна b~=34 и полным размером М =50. Установленный для результатов шаг по частоте 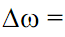0.1 несколько выше фактической разрешающей способности 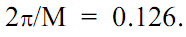Для обеспечения работы оконной функции по всему интервалу сигнала задавались начальные и конечные условия вычислений (продление обоих концов сигнала нулевыми значениями на M точек).

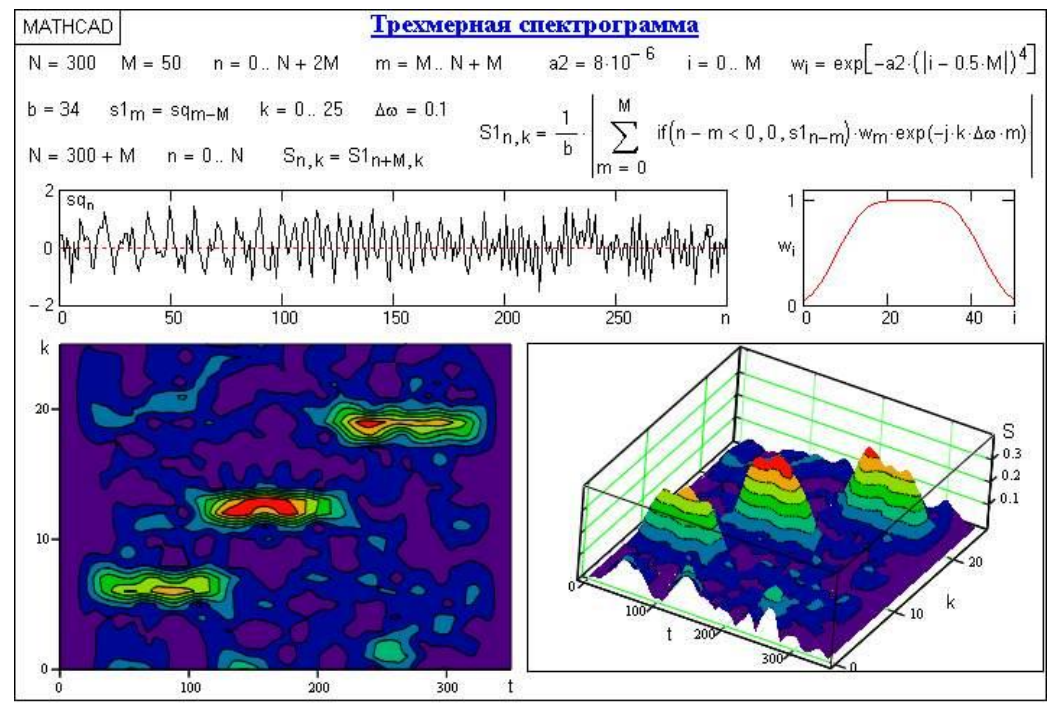
Рисунок 3.3 – Пример представления частотно-временной спектрограммы

Как видно по результатам вычислений, оконное преобразование позволяет

выделить информативные особенности сигнала и по времени, и по частоте. Разрешающая способность локализации определяется принципом неопределенности Гейзенберга, который гласит, что невозможно получить произвольно точное частотно-временное представление сигнала. Чем уже окно, тем лучше временное разрешение, но хуже частотное, и наоборот.

На рис. 3.4 приведен пример частотно-временного оконного преобразования

сигнала, состоящего из 4-х непересекающихся интервалов, в каждом из которых сумма двух гармоник разной частоты.

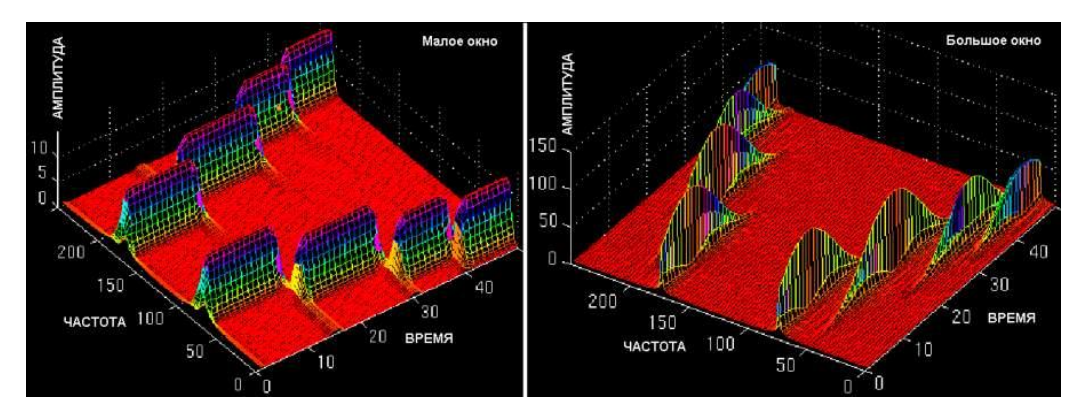
Рисунок 3.4 – Пример частотно-временного оконного преобразования сигнала

В качестве окна применена гауссова функция разной ширины. Узкое окно обеспечивает лучшее временное разрешение и четкую фиксацию границ интервалов, но широкие пики частот в пределах интервалов. Широкое окно напротив – четко отмечает частоты интервалов, но с перекрытием границ временных интервалов. При решении практических задач приходится выбирать окно для анализа всего сигнала, тогда как разные его участки могут требовать применения разных окон. Если сигнал состоит из далеко отстоящих друг от друга частотных компонент, то можно пожертвовать спектральным разрешением в пользу временного, и наоборот.