Векторное произведение.
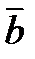
|
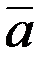
|
| j |
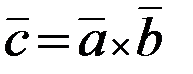
|
| Рис. 1.6 |
1) |`с | = с = ab sin j (площади параллелограмма, построенного на `а и`b; j– угол между векторами)
2) `с перпендикулярен `а и`b
3) векторы`а,`b,`с после приведения к общему началу образуют (так же как `i,` j, `к) правую тройку векторов.
(Это значит, что если смотреть с конца вектора`сна векторы `аи `b, то вектор `а для совмещения с вектором `b поворачивается против часовой стрелки через наименьший угол.)
Свойства векторного произведения.
1) `а ´`b = -`b ´`а (векторное произведение не обладает переместительным свойством).
2) `а ´`b = 0 если `а = 0, `b = 0 или `а ||`b (j = 0)
3) (m`а ) ´`b = `а ´ (m`b) = m`а ´`b (сочетательное свойство по отношению к скалярному множителю)
4) `а ´ (`b +`с ) = `а ´`b +`а ´`с (распределительное свойство)
Легко убедиться (см. свойства 1 и 2), что `i  `i = `j
`i = `j  `j = `к
`j = `к  `к = 0;
`к = 0;
`i  `j = –`j
`j = –`j  ` i = к; `j
` i = к; `j  `к = –`к
`к = –`к  `j = `i; ` i
`j = `i; ` i  `к = – `i
`к = – `i  `к = `j
`к = `j
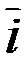
|
|

|
если два вектора перемножаются «против часовой стрелки»
(положительное направление обхода окружности) – третий
вектор получается «с плюсом»: `j ´`к =`i;если “по
часовой” – с минусом: `к ´` j = –`i.
Найдем векторное произведение, если вектора заданы своими координатами. `а ´`b = (`iax + `jay + `кaz) (`ibx + `jby + `кbz) = `i ´`iaxbx + +`j ´`iaybx +`к ´`jazbx +`i ´`jaxby +`j ´`jayby + `к ´`jazby +`j ´`к axbz + +`j ´`кaybz +`к ´`кazbz =`i (aybz – azby) – `j (axbz – azbx) +`к (axby – aybx).
Сравнив полученное выражение с (1.6), легко убедиться в том, что векторное произведение векторов `а и`b, заданных в разложении по декартову базису, удобнее всего вычислять по формуле
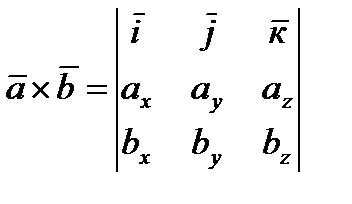 (1.22)
(1.22)
Контрольные вопросы.
1) Что называется векторным произведением векторов? Каковы его свойства и выражение через координаты векторой-сомножителей?
2) Каковы условия коллинеарности и перпендикулярности двух векторов и как они выражаются через координаты векторов?
Тест 7.
1) Определить угол между векторами 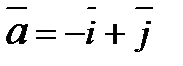 и
и 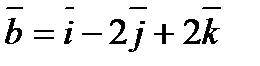 и указать верный ответ:
и указать верный ответ:
а) 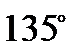 , б)
, б)  .
.
2) Вычислить площадь треугольника с вершинами А(7,3,4),В(1,0,6),С(4,5,-2) и выбрать верный ответ:
а) 24, б) 24,5.
1.5.4. Смешанное (векторно – скалярное) произведение векторов.
Смешанным произведением векторов `а,`b,`с называют скалярное произведение вектора `а ´`b на вектор `с, т.е. `а`b`с = (`а ´`b)`с(1.23)
Свойства смешанного произведения:
1) смешанное произведение равно нулю, если:
а) хоть один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) перемножаемые векторы компланарны.
2) смешанное произведение не изменится, если знаки векторного и скалярного произведения поменять местами, т.е (`а ´`b)`с = `а (`b ´`с).
3) смешанное произведение не меняется, если перемножаемые векторы переставлять в круговом порядке: `а `b`с = `b`с`а = `с`а `b
4) при перестановке двух любых векторов смешанное произведение меняет знак: `b`а `с = –`а `b`с ; `с `b`а = –`а `b`с; `а `с`b = –`а `b`с
Если векторы заданы своими координатами, то: 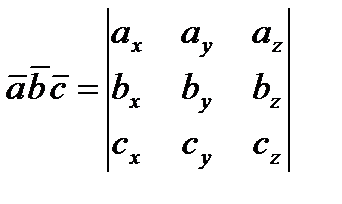 (1.24)
(1.24)
| Условие компланарности векторов принимает вид: | 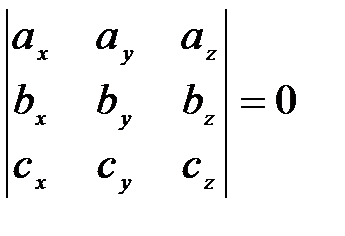
| (1.25) |
(Компланарные вектора параллельны одной плоскости; векторное произведение двух векторов даст вектор, перпендикулярный этой плоскости и, соответственно, третьему вектору и их скалярное произведение будет равно нулю).
Объемы призмы V1 и пирамиды V2 построенных на `а,`b,`с определятся так: V1 = |`а `b`с| и V2 = 1 / 6 |`а `b`с | (1.26).
Контрольные вопросы.
1) Что называется смешанным произведением векторов? Каковы его свойства и выражение через координаты векторов-сомножителей? 2) Каковы условия компланарности трёх векторов и как они выражаются через координаты векторов? Тест 8. 1) Вычислить объём пирамиды с вершинами О(0,0,0), А(5,2,0), В(2,5,0), С(1,2,4) и указать верный ответ: а) 14 куб.ед., б) 12 куб.ед. 2) Лежат ли точки А(2,-1,-2), В(1,2,1), С(2,3,0) и Д(5,0,-6)? Выбрать верный ответ и обосновать его. а) да, б) нет 1.5.5 Собственные значения и собственные векторы матрицы.Характеристическим уравнением матрицы Корни Система уравнений Пример: Найти собственные значения и собственные векторы матрицы: Теперь можно найти собственные векторы матрицы I. Используя (1.10) найдём II. (1) - разделим 3-ий столбец на 2, (2) - заменим строки столбцами, (3) - вычтем из 2-ой строки 1-ую, (4 - вычтем из 3-ей строки 2-ую, используя (1.10) найдём: . III. Аналогично вычисляется собственный вектор и для Контрольные вопросы.
1) Что называют характеристическим уравнением матрицы? 2) Что такое характеристические числа (собственные значения) матрицы? 3) Что такое собственный вектор матрицы? 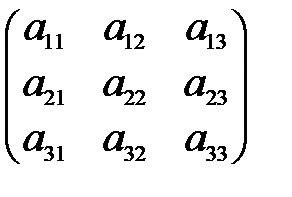 называют уравнение
называют уравнение 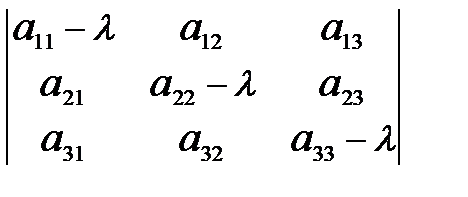 = 0 (1.27)
= 0 (1.27)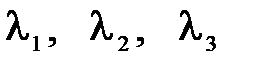 этого уравнения называют характеристическими числами (собственными значениями) матрицы.
этого уравнения называют характеристическими числами (собственными значениями) матрицы.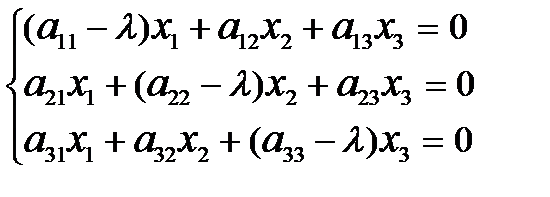 , в которой l имеет одно из значений
, в которой l имеет одно из значений 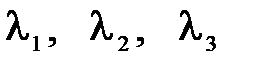 и определитель которой в силу этого равен нулю, определяет тройку чисел (х1, х2, х3), соответствующую данному характеристическому числу. Эта совокупность чисел с точностью до постоянного множителя определяет ненулевой вектор
и определитель которой в силу этого равен нулю, определяет тройку чисел (х1, х2, х3), соответствующую данному характеристическому числу. Эта совокупность чисел с точностью до постоянного множителя определяет ненулевой вектор 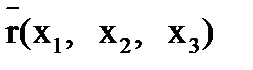 , называемый собственным вектором матрицы. Таким образом, квадратная матрица 3-его порядка имеет три собственных значения и три собственных вектора. (В общем случае среди собственных значений могут быть и кратные (одинаковые), в том числе и комплексные и мнимые. Собственные значения симметрической матрицы- только действительные числа.) Векторы эти могут быть записаны в матричной форме, в виде вектора-столбца, где t– произвольное постоянное
, называемый собственным вектором матрицы. Таким образом, квадратная матрица 3-его порядка имеет три собственных значения и три собственных вектора. (В общем случае среди собственных значений могут быть и кратные (одинаковые), в том числе и комплексные и мнимые. Собственные значения симметрической матрицы- только действительные числа.) Векторы эти могут быть записаны в матричной форме, в виде вектора-столбца, где t– произвольное постоянное
число. 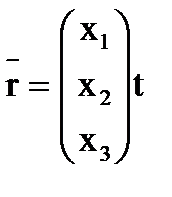 (1.28)
(1.28)
(Зачастую его удобнее использовать, чем уже привычный вектор-строку).
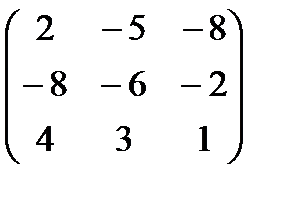 . Характеристическое уравнение матрицы примет вид:
. Характеристическое уравнение матрицы примет вид: 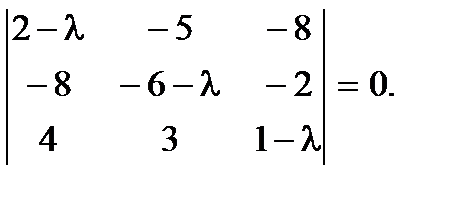 Раскроем определитель по элементам первой строки
Раскроем определитель по элементам первой строки 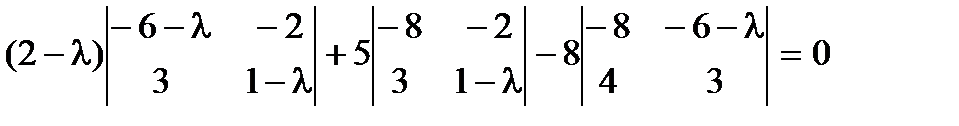
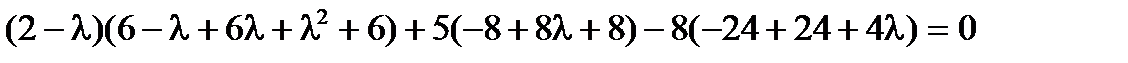
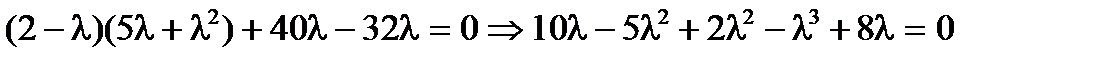
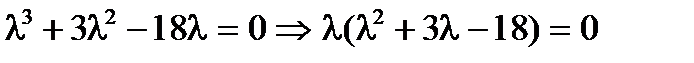
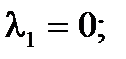
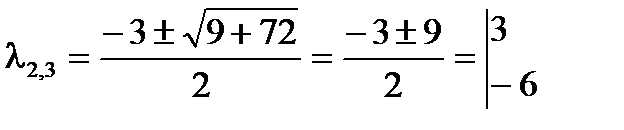
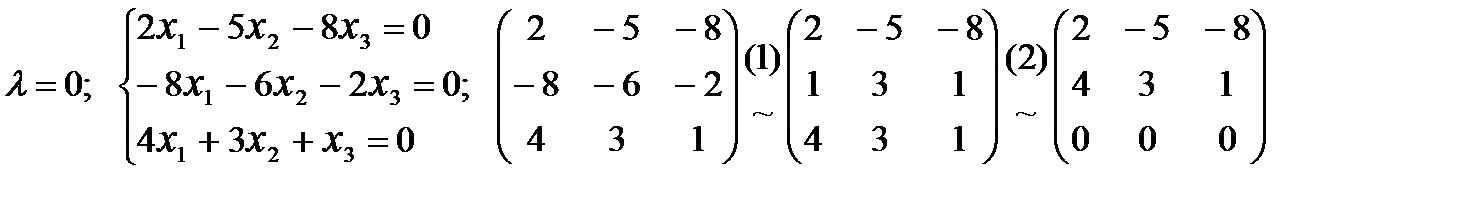
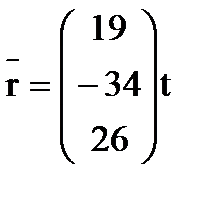
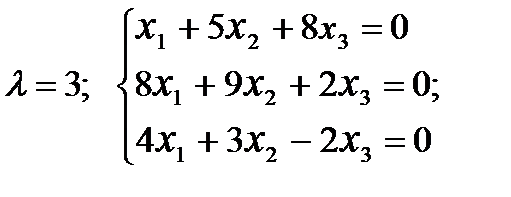
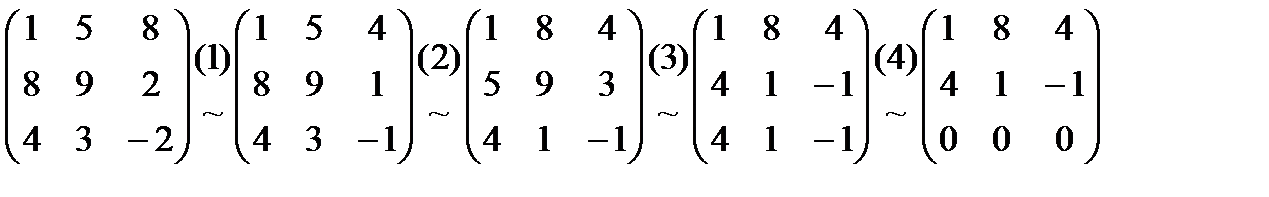
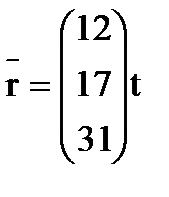
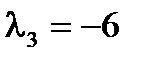 .
.
Дата добавления: 2016-04-14; просмотров: 1312;
