Базовые логические элементы
Применение двоичной системы счисления в цифровой электронике обеспечивает более высокую скорость выполнения операций и более высокую надежность электронной аппаратуры, т.к. элементной базой для ее построения служат элементы с двумя устойчивыми состояниями. Для описания алгоритмов работы цифровых устройств используется соответствующий математический аппарат, получивший название булевой алгебры или алгебры логики. Основным понятием алгебры логики является высказывание.
Высказывание – некоторое предположение, о котором можно утверждать, что оно истинно или ложно. Любое высказывание можно обозначить символом х и считать, что х = 1, если высказывание истинно, и х = 1, если высказывание ложно.
Логическая переменная – такая величина х, которая может принимать только два значения: 0 или 1.
Переключательная (логическая) функция – функция y = f(x1, x2,…, xn), которая так же, как и ее аргументы х1, х2, …, хn, может принимать значения 0 или 1. При технической переключательных функций логические переменные отожествляются с входными сигналами логических элементов, а значения переключательной функции – с выходными сигналами.
Любую логическую функцию можно задать с помощью таблицы истинности. Задать логическую функцию – означает указать значения функции при всех возможных комбинациях значений аргументов.
Каждую конкретную комбинацию значений аргументов называют набором. При n аргументах существует 2n наборов. Для краткости набор записывается в виде двоичного числа, цифрами которого являются значения переменных, расположенных в определенном порядке. Двоичное число, представляющее набор, называется номером набора и обозначается α..
При n аргументах совокупность всех значений функции на 2n наборах содержит 2n нулей и единиц. Каждой функции соответствует своя комбинация этих 2n значений. Общее количество всех возможных функций n аргументов определяется числом 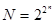 .
.
Логические функции одной переменной приведены в табл. 3,
где f0 – константа нуля;
f1 – тождественная функция;
f2 – логическое отрицание (функция НЕ);
f3 – константа единицы.
Таблица 3
| α | х | f0 | f1 | f2 | f3 |
Логические функции двух переменных приведены в табл. 4. В данном случае n = 2, поэтому число наборов переменных 2n = 4, а число всех возможных переключательных функций 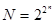 = 16.
= 16.
Таблица 4
| α | х1 | х0 | y = f(x1, x0) | |||||||||||||||
| f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | |||
Дизъюнкция (логическое сложение) – функция y = f14(x1, x0) = x1 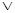 x0, которая истинна тогда, когда истинны или х1, или х0, или обе переменные. Дизъюнкцию также называют функцией ИЛИ. Устройство, предназначенное для реализации логического сложения, называют логическим элементом ИЛИ, условное обозначение которого показано на рис. 1,а.
x0, которая истинна тогда, когда истинны или х1, или х0, или обе переменные. Дизъюнкцию также называют функцией ИЛИ. Устройство, предназначенное для реализации логического сложения, называют логическим элементом ИЛИ, условное обозначение которого показано на рис. 1,а.
Конъюнкция (логическое умножение) - функция y = f8(x1, x0) = x1  x0, которая истинна только тогда, когда истинны х1 и х0. Эта функция называется также функцией И. Устройство, предназначенное для реализации логического умножения, называется логическим элементом И, условное обозначение которого показано на рис. 1,б.
x0, которая истинна только тогда, когда истинны х1 и х0. Эта функция называется также функцией И. Устройство, предназначенное для реализации логического умножения, называется логическим элементом И, условное обозначение которого показано на рис. 1,б.
Функция Пирса - функция y = f1(x1, x0) = x1 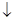 x0 =
x0 = 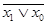 , которая истинна только тогда, когда х1 и х0 ложны. Эта функция также называется функцией ИЛИ-НЕ (отрицанием дизъюнкции). Устройство, предназначенное для реализации функции Пирса, называется логическим элементом ИЛИ-НЕ, условное обозначение которого показано на рис. 1,в.
, которая истинна только тогда, когда х1 и х0 ложны. Эта функция также называется функцией ИЛИ-НЕ (отрицанием дизъюнкции). Устройство, предназначенное для реализации функции Пирса, называется логическим элементом ИЛИ-НЕ, условное обозначение которого показано на рис. 1,в.
Штрих Шеффера - функция y = f7(x1, x0) = x1|x0 = 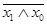 , которая ложна только тогда, когда х1 и х0 истинны. Эта функция называется также функцией И-НЕ (отрицание конъюнкции). Устройство, предназначенное для реализации этой функции, называется логическим элементом И-НЕ, условное обозначение которой показано на рис. 1,г.
, которая ложна только тогда, когда х1 и х0 истинны. Эта функция называется также функцией И-НЕ (отрицание конъюнкции). Устройство, предназначенное для реализации этой функции, называется логическим элементом И-НЕ, условное обозначение которой показано на рис. 1,г.
Функция равнозначности - функция y = f9(x1, x0) = x1~x0, которая истинна, когда значения истинности х1 и х0 совпадают, и ложна, когда значения истинности х1 и х0 не совпадают.
Функция неравнозначности - функция y = f6(x1, x0) = x1 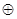 x0, которая истинна, когда значения истинности х1 и х0 не совпадают, и ложна, когда значения истинности х1 и х0 совпадают. Эту функцию называют также функцией отрицания равнозначности, функцией ИЛИ-ИЛИ или функцией сложения по модулю 2 (mod 2).
x0, которая истинна, когда значения истинности х1 и х0 не совпадают, и ложна, когда значения истинности х1 и х0 совпадают. Эту функцию называют также функцией отрицания равнозначности, функцией ИЛИ-ИЛИ или функцией сложения по модулю 2 (mod 2).
Функция импликации - функция y = f11(x1, x0) = x1→x0, которая ложна в том и только в том случае, когда х1 истинна, а х0 ложна.
Функция y = f13(x1, x0) = x0→x1 также является функцией импликации.
Функция запрета – функция y = f4(x1, x0) = x1 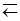 x0, которая истинна в том и только в том случае, когда х1 истинна, а х0 ложна.
x0, которая истинна в том и только в том случае, когда х1 истинна, а х0 ложна.
Функция y = f2(x1, x0) = x0 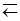 x1 также является функцией запрета.
x1 также является функцией запрета.
Функции y = f0(x1, x0) = 0 и y = f15(x1, x0) = 1 являются константами.
Функции y = f3(x1, x0) =, y = f5(x1, x0) =, y = f10(x1, x0) =, y = f12(x1, x0) = зависят только от одной переменной и не представляют интереса.
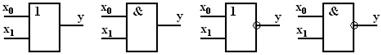
а) б) в) г)
Рисунок 1
Переключательная функция составляется на основании таблицы истинности, при этом она записывается или в совершенной дизъюнктивной нормальной форме (СДНФ), или в совершенной конъюнктивной нормальной форме (СКНФ).
СДНФ переключательной функции составляется следующим образом: для каждого набора, на котором функция равна 1, записывается конъюнкция всех аргументов, причем, если аргумент в этом наборе принимает значение 0, то пишется его отрицание. Затем производится логическое сложение всех конъюнкций.
Например, СДНФ переключательной функции И-НЕ (табл. 4) записывается в виде
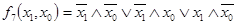 . (1)
. (1)
Для составления СКНФ переключательной функции необходимо: для каждого набора, на котором функция равна 0, записать дизъюнкцию всех аргументов, причем, если аргумент в этом наборе принимает значение 1, то пишется его отрицание. Затем производится логическое умножение этих дизъюнкций.
СКНФ переключательной функции ИЛИ-НЕ (таблица 4) записывается в виде
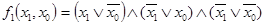 . (2)
. (2)
Дата добавления: 2016-02-16; просмотров: 1566;
