Преобразователи кодов, шифраторы и дешифраторы

Преобразователи кодов, шифраторы и дешифраторы относятся к комбинационным узлам.

Преобразователи кодов. Для представления информации используются разнообразные двоичные и двоично-десятичные коды: прямой, обратный, дополнительный и др. поэтому в цифровых системах широко применяются преобразователи кодов, обеспечивающие перевод информации из одной формы в другую.

Наиболее простую структуру имеет преобразователь чисел из прямого кода А = а_k…a₁a₀ в обратный B = b_k…b₁b₀, который в соответствии со значением знакового разряда Z переводит отрицательное число (Z = 1) в обратный код: 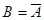, а положительное число (Z = 0) передает на выход без изменения: В = А. Таким образом, в каждом i-том разряде преобразователя (i = 0, 1, 2, …, k) выполняется логическая операция

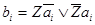. (1)

Шифраторы и дешифраторы. Одними из основных видов преобразования информации в цифровых системах являются шифрация и дешифрация. Шифрацией называется преобразование m-разрядного двоичного кода, имеющего k_m безразличных наборов входных переменных, в однозначно соответствующий ему n-разрядный код, имеющий меньшее число разрядов n < m и безразличных наборов k_n < k_m. В результате шифрации осуществляется «сжатие» информации для передачи по меньшему числу линий связи за счет полного (при k_n = 0) или частичного (при k_n ≠ 0) исключения безразличных наборов. Обратное преобразование, т.е. восстановление информации в первоначальном m-разрядном коде с k_m избыточными комбинациями, называется дешифрацией. Функциональные узлы для выполнения этих операций называются шифраторами и дешифраторами. Они различаются по числу входов и выходов и называются «шифратор (дешифратор) из m в n».

Таблица истинности шифратора «из 10 в 4» приведена в табл. 1, таблица истинности дешифратора «из 3 в 8» - в табл. 2.

В цифровых системах шифраторы используются для передачи информации между различными устройствами при ограниченном числе линий связи, а также преобразования вводимых чисел в двоичную форму.

Таблица 1

Таблица 2