Аналого-цифровые преобразователи
Аналого-цифровой преобразователь (АЦП) преобразует аналоговый сигнал в цифровой. Далее описываются некоторые типы АЦП.
4.4. АЦП последовательного счета:
Принцип такого преобразователя сводится к следующему. Счетные импульсы заполняют счетчик, на выходе которого формируется код с нарастающим весом. Этот код поступает на ЦАП, напряжение на выходе которого увеличивается. Когда оно чуть превысит напряжение, присутствующее в данный момент на входе, доступ импульсов к счетчику прекращается. Код, установившийся при этом на выходах счетчика, является цифровым эквивалентом напряжения на выходе ЦАП, а следовательно, и напряжения выборки входного напряжения Uвх.
Схема, реализующая описанный принцип АЦП последовательного счета, изображена на рис.23,а.
Рис. 23. АЦП последовательного счета
Преобразование начинается с обнуления счетчика импульсом генератора тактовых импульсов (ГТИ). Период следования этих импульсов является периодом дискретизации входного аналогового напряжения. После обнуления счетчика напряжение на выходе ЦАП становится равным нулю – на выходе компаратора логическая 1, обеспечивающая поступление импульсов от генератора счетных импульсов (ГСИ) через элемент & на счетчик. Когда напряжение на выходе ЦАП станет практически равным Uвх, компаратор переключится и логическим нулем на выходе разъединит ГСИ и счетчик. Таким образом, в промежуток времени с момента окончания импульса ГСИ, обнулившего счетчик, до завершения преобразования осуществляется оцифровка выборки входного напряжения.
Заметим, что с поступлением на счетчик каждого импульса (с увеличением выходного кода на единицу) напряжение на выходе ЦАП увеличивается на квант, так что Uвых.цапсодержит целое число квантов, которым оно уравновешивает Uвх. Поэтому нельзя гарантировать, что такое уравновешивание может иметь ошибку, меньшую одного кванта, что соответствует ошибке на единицу в младшем разряде выходного кода.
Условное изображение АЦП приведено на рис. 23,б, где для общности показаны только входной и выходные выводы.
4.5. Время-импульсный АЦП:
Времяимпульсный метод преобразования заключается в том, что входному напряжению Uвх ставится в соответствие временной интервал, длительность которого пропорциональна Uвх. Этот интервал заполняется импульсами стабильной частоты. Число их и представляет цифровой эквивалент преобразуемого напряжения. Схема, реализующая указанный принцип, изображена на рис. 24, а. Импульс с выхода генератора тактовых импульсов - ГТИ (импульсов дискретизации) обнуляет счетчик, запускает генератор линейно изменяющегося напряжения (ГЛИН) и переключает триггер в состояние Q=1. Сигналом Q=1 генератор счетных импульсов (ГСИ) через элемент & подключается к счетчику. Когда нарастающее напряжение ГЛИН станет равным выборке преобразуемого напряжения Uвх, на выходе компаратора появится логическая 1, которая переключит триггер в состояние Q=0 и прервет связь ГСИ со счетчиком. Код, установившийся на выходе счетчика, – цифровой эквивалент выборки Uвх. Следующая выборка задаст свой код на выходах счетчика.
Рис. 24.ВремяимпульсныйАЦП
Чтобы обеспечить линейность нарастания напряжения, заряд конденсатора в генераторах ЛИН осуществляется током неизменной величины, что обеспечивается специальными схемами стабилизации.
Временные диаграммы на рис. 24,б иллюстрируют описанные процессы. На выходе триггера формируются «временные ворота». Начало их соответствует тактовому импульсу с ГТИ, а конец – появлению 1 на выходе компаратора, когда наступает равенство напряжений ГЛИН и выборки. Таким образом, длительность «временных ворот» пропорциональна текущему значению входного напряжения. «Временные ворота» заполняются счетными импульсами стабильной частоты, поэтому их число пропорционально значению текущей выборки Uвх. Только в частном случае во «временные ворота» может точно уложиться целое число периодов Тсчсчетных импульсов. Может оказаться, 4 что между последним вошедшим в ворота импульсом и границей ворот будет интервал, почти равный Тсч, т.е. следующий импульс генератора будет чуть правее конечной границы ворот (см. временные диаграммы на рис 17), и не поступит на счетчик. Поэтому нужно считаться с тем, что выходной код времяимпульсного преобразователя может иметь погрешность в одну единицу (единицу в младшем разряде).
4.6. Кодоимпульсный АЦП:
В описанных АЦП цифры (0 или 1) в разрядах выходного кода могут в процессе преобразования многократно изменяться, так как устанавливаются в ходе постепенного накопления числа в счетчике.
При рассматриваемом преобразовании формируемый код последовательно приближается к своему полному выражению: вначале определяется цифра в старшем n-ом разряде, затем в (n–1)-ом и т.д. до младшего разряда.
Такая возможность формирования основана на свойствах натурального двоичного кода: веса единиц в соседних разрядах отличаются вдвое; единица в старшем разряде имеет вес, больший половины веса всего кода; единица в соседнем разряде имеет вес, больший четверти веса всего кода, и т. д. Например, вес кода 11112равен 15; вес единицы в четвертом разряде равен 8, что больше 0,5×15; вес единицы в третьем разряде равен 4, что больше 0,25×15, и т.д. Поэтому для определения цифры в старшем разряде формируемого кода надо сравнить Uвхс 0,5Um- половиной максимального для данного АЦПзначения Uвх. Если окажется, что Uвх<0,5Um, то в старшем разряде кода – цифра 0, и дальнейшее сравнение Uвхнадо производить с 0,25Um. Если же Uвx>0,5Um, то в старшем разряде кода цифра 1; при этом последующее сравнение следует производить с (1/2+1/4)Umи т.д.
На рис. 25 изображена схема устройства, реализующая изложенный принцип. Код, соответствующий выборке входного аналогового сигнала, формируется на выходах регистра кода РК. В каждый разряд этого регистра, начиная со старшего разряда, по входам S последовательно записывается логическая 1 с соответствующего выхода сдвигового регистра РС. Одновременно она поступает на верхний (по схеме) вход конъюнктора К, принадлежащий данному разряду РК. Каждая записанная 1 «испытывается» на соответствие выборке входного сигнала. Для этого код с выходов РК в процессе формирования преобразуется цифроаналоговым преобразователем в напряжение (UЦАП), которое сравнивается на аналоговом компараторе с выборкой преобразуемого напряжения Uвх. Если Uвх>UЦАП, то на выходе компаратора присутствует логический 0, и после конъюнкторов Кn…К1на входах R регистра РК – логические нули, которыми разряды РК не сбрасываются: в проверяемом разряде остается записанной 1. Если Uвх<UЦАП, то на выходе компаратора логическая 1 – на обоих входах компаратора проверяемого разряда логические единицы, которыми этот разряд сбрасывается в нуль, остальные разряды кода сохраняются.
Рис.25КодоимпульсныйАЦП
Логическая 1 на выходах РС появляется поочередно: на выходе n - с приходом тактового импульса (импульса дискретизации входного аналогового сигнала) на вход Dn, на выходах n–1, n–2,... – в момент окончания сдвигающего импульса на динамическом входе С.
Очередной цикл преобразования выборки входного сигнала начинается с поступлением тактового импульса; кроме записи 1 в старший n-ый разряд РК он обнуляет все его остальные разряды (по второму входу R), записывает 1 по входу Dn в n-й разряд PC, а также переключает триггер циклов в состояние 1, после чего сдвигающие импульсы начинают поступать на C-вход PC. В конце цикла (после сформирования выходного кода) логической 1 с выхода первого разряда PC триггер цикла переключается в 0 и цепь связи ГСИ - PC прерывается. С поступлением следующего тактового импульса начинается цикл преобразования следующей выборки входного сигнала.
Заметим, что в соответствии с методом преобразования рассмотренный АЦПназывают преобразователем поразрядного кодирования.
Пример:
Определим код на выходе рассмотренного АЦП при следующих данных: Uвх = 8,5 В, разрядность АЦП n = 10, опорное напряжение АЦП Uоп =10,24 В.
Напряжение Uопделится квантованными уровнями на 2n-1 квантов, величина каждого из которых ΔU =Uоп / 2n-1.
В данном случае ΔU = 10,24/1024-1≈ 10,24 / 1024=10мВ.
Такое приращение ΔUцап выходное напряжение цифроаналогового преобразователя (в структуре АЦП) получает от приращения входного кода на единицу (от единицы в младшем разряде кода). Приращение напряжения Uцапот единицы в k-ом разряде равно величине кванта (в данном случае 10мВ), умноженной на вес единицы в этом разряде.
Ниже приведены вес единицы в разрядах 10-разрядного кода и напряжение, которое она добавляет к Uцап
Таблица 1
| # разряда | Вес единицы | ΔUцап,В |
| 5,12 | ||
| 2,56 | ||
| 1,28 | ||
| 0,64 | ||
| 0,32 | ||
| 0,16 | ||
| 0,08 | ||
| 0,04 | ||
| 0,02 | ||
| 0.01 |
В соответствии с алгоритмом работы кодоимпульсного АЦП проведем сравнение Uвхс значениями ΔUцап, компенсирующими напряжение Uвх. Если Uвх > Uцап, то против соответствующего неравенства будет проставлена единица.
Таблица 2
| 8,5> 5,12 | |
| 8,5> 5,12+2,56=7,68 | |
| 8,5< 7,68+1,28=8,96 | |
| 8,5> 7,68+0,64=8,32 | |
| 8,5< 8,32+0,32=8,64 | |
| 8,5> 8,32+0,16=8,48 | |
| 8,5< 8,48+0,08=8,56 | |
| 8,5< 8,48+0,04=8,52 | |
| 8,5= 8,48+0,02=8,50 |
Таким образом, код на выходах АЦП N=11010100102= 85010. Учитывая, что каждая единица кода соответствует кванту в 10 мВ, фиксируем входное напряжение равным 8,5 В.
4.7. АЦП двойного интегрирования:
В таких АЦП процесс преобразования имеет две стадии. На первой из них в течение фиксированного временного интервала T1интегрируется входное напряжение Uвх. Чем оно больше, тем большего значения достигает напряжение на конденсаторе C интегратора за время T1.
При этом конденсатор заряжается через регистр R1неизменным током Iз=Uвх / R1, получая заряд Qз= UвхT1/ R1.
На второй стадии на интегратор подается образцовое напряжение U0с полярностью, обратной полярности Uвх, и конденсатор интегратора через резистор R2разряжается неизменным током Iр=U0/R2.
Как только напряжение на интеграторе достигает нулевого значения, элементы схемы прекращают вторую стадию – преобразование закончено.
В течение второй стадии конденсатор интегратора теряет заряд
Qр=U0T2/R2,
где T2– продолжительность второй стадии, за которую конденсатор разряжается до нуля.
Так как на первой стадии конденсатор заряжался от нуля до некоторого значения, пропорционального Uвх, а во второй стадии от этого значения разряжался до нуля, то приобретенный и потерянный заряды равны:
UвхT1/ R1= U0T2/R2, Uвх=U0T2R1/ T1R2
Таким образом, входное преобразуемое напряжение Uвхпропорционально длительности второй стадии.
Фиксированный интервал T1задается с помощью счетчика, который из обнуленного состояния к началу первой стадии заполняется импульсами тактового генератора с периодом Tт, и в момент его переполнения (обнуления) эта стадия заканчивается, т. е.
T1= TтNmax,
где Nmax–максимальное число, которое может вместить счетчик.
В интервале T2на этот счетчик поступают импульсы того же генератора до тех пор, пока напряжение на выходе интегратора не станет равным нулю. Поэтому при N импульсах, поступивших на счетчик во второй стадии,
T2=NTт и Uвх= U0T2R1/ T1R2= U0NTт R1/ TтNmax R2=U0N R1/Nmax R2.
Так как U0, R1, R2и Nmaxявляются постоянными параметрами схемы, то входное преобразуемое напряжение выражается числом импульсов N, поступивших на счетчик во второй стадии.
Если длительность T1первой стадии выбрать кратной периоду напряжения питающей сети, то результат его интегрирования будет равен нулю, т.е. сетевая помеха будет отсутствовать.
Структурная схема АЦП двойного интегрирования приведена на рис. 26. На первой стадии (продолжительностью T1) устройство управления (УУ), воздействуя на переключатель, подключает к интегратору входное напряжение и открывает доступ импульсов тактового генератора (ГТИ) к счетчику времени первой стадии. Когда в этот счетчик будет занесено число, соответствующее времени T1, он даст сигнал на устройство управления, которое подключит к интегратору образцовое напряжение U0, и даст разрешение на подключение ГТИ к счетчику результата измерения. После этого конденсатор интегратора будет разряжаться, и когда напряжение на его выходе окажется практически равным нулю, УУ разъединит ГТИ и счетчик результата измерения. Занесенное в него число будет пропорционально входному напряжению.
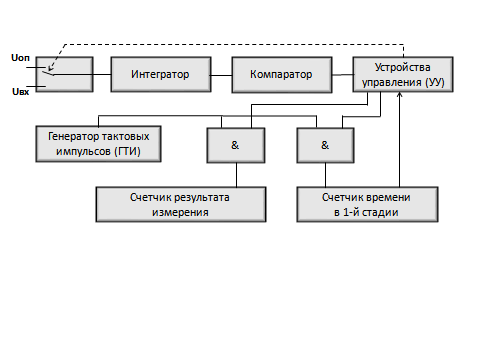
Рис. 26.АЦП двойного интегрирования
Нестабильность частоты тактового генератора (если только частота не меняется во время преобразования) не влияет на точность: в выражении Uвхпериод Tт не входит. Вместе с этим АЦП двойного интегрирования не отличается высоким быстродействием, что связано с наличием временных стадий T1и T2, в течение которых осуществляется интегрирование.
4.8. Параметры АЦП и ЦАП:
К основным параметрам АЦП и ЦАП следует отнести максимальное напряжение Umax(входное для АЦП и выходное для ЦАП), число разрядов кода n, разрешающую способность и погрешность преобразования.
Разрешающая способность. Под разрешающей способностью (РС) понимают наименьшее значение входной величины, различаемое устройством, т.е. в той или иной форме фиксируемое им на выходе. Численно РС оценивают различимым приращением выходной величины от наименьшего возможного приращения входной величины.
Разрешающая способность для ЦАП - приращение выходного напряжения от приращения входного кода на единицу в младшем разряде Это - наименьшее приращение (квант - Δu), какое может получить напряжение на выходе цифроаналогового преобразователя.
Δu= Uоп / 2n-1,
где 2n–1 - максимальный вес входного кода, n – разрядность ЦАП.
Так, при Uоп =10,24 В, n = 12 Δu = 10,24 / (212-1) ≈ 2,5 мВ. Чем больше n, тем меньше Δu и тем точнее выходное напряжение представляет входной код.
Относительное значение разрешающей способности
δ= Δu /Uоп = 1/2n-1.
Тот же параметр АЦП определяется приведенными выражениями и представляет собой приращение входного напряжения, которое вызывает приращение выходного кода на единицу в младшем разряде. Меньшее приращение входного напряжения АЦП не почувствует, т.е. квант Δu – наименьшее приращение входного напряжения, различимое АЦП. В соответствии с этим разрешающую способность отождествляют с чувствительностью АЦП.
Быстродействие ЦАП и АЦП оценивается временем преобразования tпр, которое определяется методом преобразования и быстродействием элементной базы. Так, например, в АЦП последовательного счета (Рис. 6,а) счетчик с большим быстродействием позволит увеличить частоту генератора счетных импульсов, что уменьшит tпр. Время преобразования такого АЦП линейно зависит от величины входного напряжения Uвх: чем оно больше, тем большее число счетных импульсов должно поступить на счетчик, чтобы напряжение с выхода ЦАП уравновесило входное напряжение. Если Uвхимеет значение, равное максимальному входному напряжению для данного АЦП, то за время tпр на счетчик поступит 2n-1 импульсов с периодом Tсч и время преобразования составит
tпр= (2n-1) Tсч.
При больших входных напряжениях большим быстродействием обладают кодоимпульсные АЦП.
Выбор ЦАП может, в частности, производиться по значению tпр: за время tпркод на входе не должен, например, измениться более, чем на единицу в младшем разряде. АЦП с большим временем преобразования не может работать с быстро изменяющимся входным напряжением, так как последнее за время tпр может измениться.
Для АЦП период дискретизации Тд следует выбирать больше tпр: Тд>tпр, т.е. между скоростью преобразования 1/tпри частотой дискретизации (Fд=1/Тд) должно соблюдаться соотношение 1/tпр>Fд. С другой стороны, по теореме Котельникова Fдсвязана с наивысшей частотой fmaxв спектре непрерывного входного сигнала неравенством Fд≥2fmax. Поэтому АЦП должен иметь время преобразования tпр<1/2fmax.
Наибольшим быстродействием обладают АЦП с параллельным преобразованием, в котором входное напряжение сравнивается одновременно с 2n -1 уровнями, для чего структура преобразователя, кроме прочего, содержит 2n -1 аналоговых компараторов и приоритетный шифратор. Во избежание усложнения структуры такого преобразователя число его разрядов не должно быть большим (в 8-ми разрядном АЦП количество компараторов составляет 28–1=255), что дополнительно снижает возможную точность преобразования.
Погрешность преобразования имеет статическую и динамическую составляющие. Статическая составляющая включает в себя методическую погрешность квантования, или дискретности и инструментальную погрешность от неидеальности элементов преобразователей. Погрешность квантования Δкобусловлена самим принципом представления непрерывного сигнала квантованными уровнями, отстоящими друг от друга на выбранный интервал. Выше эта погрешность описывалась. Для ее уменьшения напряжение на входе (для АЦП) и на выходе (для ЦАП) исходно смещают на половину кванта. При этом погрешность квантования составляет половину разрешающей способности, и в общем случае
Δк = ± 0,5Δu δ=± 0,5/ 2n—1
Инструментальная погрешность не должна превышать погрешность квантования. При этом полная абсолютная и относительная статические погрешности
Δк = ± Δu δ=± 1 / 2n—1,
что соответствует разрешающей способности преобразователя.
Динамическая составляющая погрешности связана с быстродействием преобразователя (с временем преобразования tпр) и скоростью изменения входного сигнала (V). Чем меньше tпри V, тем меньше эта составляющая. При большом tпрнужно будет увеличивать период Tд, чтобы избежать значительных динамических искажений. Для их уменьшения обычно выбирают АЦПс таким временем преобразования tпр, за которое входной сигнал изменяется не более, чем на разрешающую способность Δu = Uоп / (2n -1).
В заключение раздела отметим основные свойства рассмотренных ЦАП и АЦП:
· Из за наличия аналоговых ключей (по числу разрядов) ЦАП с матрицей R-2R имеют достаточно сложную структуру и относительно высокую стоимость, но при этом обладают наибольшей точностью.
· ЦАП с матрицей двоично взвешенных резисторов осуществляют преобразование с большей погрешностью, т.к. должного соотношения номиналов резисторов получить не удается. Однако при этом они обладают простой структурой и малой стоимостью.
· Наиболее простую структуру имеют АЦП последовательного счета, наиболее сложную - АЦП с параллельным преобразованием, компенсируя это наибольшим быстродействием.
· Значительную часть выпускаемых АЦП составляют аналогоцифровые преобразователи с поразрядным кодированием (кодоимпульсные) и двойного интегрирования. Для большинства применений они обладают достаточной точностью, быстродействием и относительно низкой стоимостью.
Дата добавления: 2016-04-02; просмотров: 3239;
