Демультиплексоры – дешифраторы
Демультиплексоры в функциональном отношении противоположны мультиплексорам. Здесь сигналы с одного информационного входа распределяются в желаемой последовательности по нескольким выходам. Выбор нужной выходной шины, как и в мультиплексоре, обеспечивается кодом на адресных входах. При т адресных входах демультиплексор может иметь в зависимости от конструкции до 2m выходов.
Идею работы демультиплексора поясняет рисунок 2.15. Вход Х− информационный, вход А – адресный, потенциал на этом входе определяет, на каком из выходов будут формироваться сигналы, повторяющие Х. Когда А = 1, верхний элемент И заперт и на выходе его F0=0; нижний элемент, напротив, открыт и работает как повторитель информационных сигналов. При А = 0 заперт нижний элемент, а верхний пропускает входную информацию. Логическая структура простого демультиплексора вида 1 : 4 представлена на рисунке 2.16.
Здесь В и А – адресные входы, X – информационный вход, V – разрешающий.




 Работу устройства описывают следующие Булевые уравнения:
Работу устройства описывают следующие Булевые уравнения:






 F0 = (Х v V) B A; F1 = (Х v V) B A; F2 = (Х v V) B A; F3 = (Х v V) B A.
F0 = (Х v V) B A; F1 = (Х v V) B A; F2 = (Х v V) B A; F3 = (Х v V) B A.
Таблица истинности, отражающая состояния входных и выходных сигналов демультиплексора (таблица 2.8).
Таблица 2.8−Входные и выходные сигналы демультиплексора
| Входы | Выходы | ||||||
| В | А | х | V | F0 | F1 | F2 | F3 |
        
    
 
|
| 0/1 0/1 0/1 0/1 x x x x | 0/1 | 0/1 | 0/1 | 0/1 |


Рис. 2.15−Принцип действия Рис. 2.16 −Логическая структура демультиплексора. демультиплексора вида 1: 4.
Дешифратором (декодером) называют устройство с несколькими входами и выходами, у которого определенным комбинациям входных сигналов соответствует активное состояние одного из выходов. Дешифратор,
следовательно, можно рассматривать как обращенный по входам демуль-типлексор, у которого адресные входы стали информационными, а бывший информационный вход, на который подается напряжение определенного уровня (U° или U1), поддерживает напряжение выходных выводов в активном состоянии.
Цифровые компараторы (устройства сравнения)
Цифровые компараторы относятся к арифметическим устройствам. Цифровые компараторы (от англ, compare − сравнивать, сличать) выполняют сравнение двух чисел, заданных в двоичном коде. В зависимости от схемного исполнения компараторы могут определять равенство А = В (А и В — независимые числа с равным количеством разрядов) либо вид неравенства: А<В или А>В. Результат сравнения отображается соответствующим логическим уровнем на одном из трех выходов. Схема одноразрядного компаратора и его графическое обозначение показаны на рисунках 2.17, 2.18. Цифровые компараторы применяются для поиска числа (слова) в потоке цифровой информации, в часовых приборах для отметки времени, при выполнении условных переходов. Логическая схема, выполняющая операцию «эквивалентность» F=AB \/ AB, может быть использована как однораз рядный компаратор.
Она представляет собой развернутую логическую структуру логического элемента « исключающее ИЛИ - НЕ» с тремя выходами. Из определения операции «исключающее ИЛИ» вытекает, что
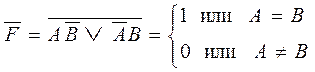
При А>В (это означает, что A=1, В=0), С = A 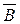 =1;
=1;
если A< В (A = 0, В = 1), то D = 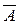 B =1.
B =1.
Два п−разрядных двоичных числа равны, когда попарно равны между собой все разряды этих чисел. Если, например, числа A и В — четырехразрядные, то признаком их равенства будет A3=В3 и А2=В2; A1=B1 и А0=В0. Применяя элемент сравнения для каждого разряда, факт равенства обоих чисел A=B установим в случае F=F3F2F1F0=1. Если же F=0, то A¹ В.
Неравенство А>В обеспечивается в четырех случаях:
когда A3>В3(A3 и B3—старшие разряды чисел A и B) или A3=B3 и A2>В2; или A3=В3 и А2=B2, и A1>В1; или A3==В3 и A2=B2 и A1=B1 и A0>B0,
Очевидно, что для выполнения условия А<В достаточно поменять местами A и B.


Рисунок 2.17 − Логическая структура Рисунок 2.18 − Условное одноразрядного компаратора графическое обозначение
Сумматоры
Сумматоры представляют собой функциональные узлы, выполняющие операцию сложения чисел. В устройствах дискретной техники суммирование осуществляется в двоичном или, реже, двоично-десятичном коде. По характеру действия сумматоры подразделяются на две категории: комбинационные – не имеющие элементов памяти; накопительные – сохраняющие результаты вычислений.
Как последовательные, так и параллельные сумматоры строятся на основе одноразрядных суммирующих схем. Сложение чисел в последовательных сумматорах осуществляется поразрядно, последовательно во времени. В сумматорах параллельного действия сложение всех разрядов многоразрядных чисел происходит одновременно.
Полусумматор
Простейшим суммирующим элементом является полусумматор (рисунок 2.19). Он имеет два входа А и В для двух слагаемых и два выхода S сумма) и Р (перенос). Обозначением полусумматора служат буквы HS (half sum—полусумма), логические состояния элементов полусумматора приведены в таблице 2.9.
Логическая структура полусумматора такова, что состояние выхода S отображает бит суммы, а выхода Р– бит переноса. Работа полусумматора описывается следующими уравнениями: 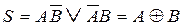 ; Р=АВ.
; Р=АВ.
 Таблица 2.9− Состояния элементов
Таблица 2.9− Состояния элементов
полусумматора
| Входы | Выходы | ||
| A | B | P | S |

 Логическая структура полусумматора в общем (а) и развернутом виде (б) показана на рисунке 3.20.
Логическая структура полусумматора в общем (а) и развернутом виде (б) показана на рисунке 3.20.
Рисунок 2.20− Логическая структура полусумматора
Полный сумматор
Полусумматор имеет два входа и пригоден поэтому для использования только в младшем разряде. Устройство для суммирования двух многоразрядных чисел должно иметь, начиная со второго разряда три входа: два для слагаемых Аi и Вi и один для сигнала переноса Pi-1 с предыдущего разряда. Этот узел можно представить как объединение двух полусумматоров (рисунок 3.21). Первый полусумматор служит для сложения двух чисел, принадлежащих одному разряду, и обеспечивает выход промежуточной суммы Si’ и переноса Pi’
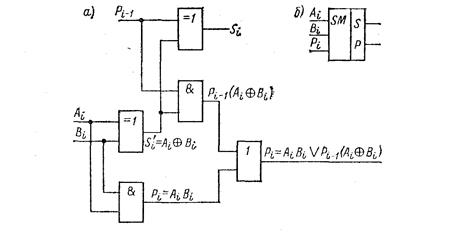
Рисунок 2.21 − Полный сумматор: а) логическая структура;
б) условное графическое изображение.
Второй полусумматор складывает перенос с предыдущего разряда Pi-1 с промежуточной суммой Si'. Функции выходов S и Р для этого случая определяются как: 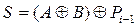 ;
; 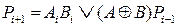 .
.
Исходя из таблицы истинности сумматора (таблица 2.10) можно написать следующие Булевы уравнения для сигналов суммы и переноса:
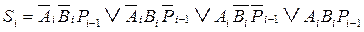 ;
;
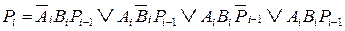 .
.
В уравнениях представлены только те члены, для которых Si=l и Pi=1, т. е. первый член функции Si относится к первой строке таблицы истинности, второй член ко второй и т. д. Сходным образом для функции Р первый член принадлежит третьей строке, второй член – пятой и так до седьмой.
| Номер | Входы | Выходы | |||
| Аi | Вi | Pi | Pi+1 | Si | |
| 7 |
Таблица 2.10 − Состояния элементов сумматора
В микросхемах-сумматорах в качестве базового узла используется сумматор (рисунок 2.22), логическая структура которого реализована на основе двух последних формул.
Как уже говорилось, суммирование многоразрядных чисел может быть последовательное либо параллельное. При последовательном вводе используется один, общий для всех разрядов полный сумматор с дополнительной цепью задержки (рисунок 2.23). Оба слагаемых кодируются последовательностями импульсов, которые синхронно вводятся в сумматор через входы A и B, начиная с младших разрядов. Цепь задержки обеспечивает хранение импульса переноса Pi+1 на время одного такта, т. е. до прихода пары слагаемых следующего разряда.


|
|
 Задержку обеспечивает D-триггер (триггер задержки). Для хранения и ввода слагаемых А и В, для преобразования последовательного кода выходных импульсов в параллельный применяют регистры сдвига. Достоинство последовательных сумматоров – малые аппаратурные затраты.
Задержку обеспечивает D-триггер (триггер задержки). Для хранения и ввода слагаемых А и В, для преобразования последовательного кода выходных импульсов в параллельный применяют регистры сдвига. Достоинство последовательных сумматоров – малые аппаратурные затраты.
 К недостаткам следует отнести сравнительно невысокое быстродействие, поскольку одновременно суммируется лишь пара слагаемых.
К недостаткам следует отнести сравнительно невысокое быстродействие, поскольку одновременно суммируется лишь пара слагаемых.
На рисунке 2.24 показана схема, поясняющая принцип действия n-разрядного параллельного сумматора с последовательным переносом.
Лекция 5
Дата добавления: 2016-02-24; просмотров: 2049;
