Группа подстановок Галуа

Рассмотрим знаменитую группу подстановок, которую исследовал выдающийся французский математик Э. Галуа (1811–1832).

Подстановкой n -й степени называется взаимно однозначное отображение множества из n элементов в себя.

Рассмотрим всего три элемента: х1, х2, х3.

Существует шесть вариантов последовательностей из трех элементов:

х1х2х3, х2х3х1, х1х3х2, х3х1х2, х2х1х3, х3х2х1.

Запишем порождение этих вариантов следующим образом:

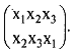
Эта запись означает, что х1переходит (отображается) в х2, х2— в х3, х3 — в x 1.

Число таких возможных подстановок равно числу вариантов последовательностей из трех элементов. Обозначим возможные подстановки:

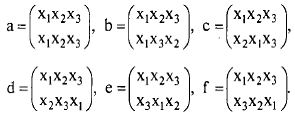
Произведением подстановок назовем последовательное выполнение сначала первой, а затем второй из перемножаемых подстановок.

Например,

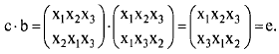
Таким образом, имеем алгебру <П, ¤>, где П — множество подстановок {а, b , с, d , e , f }, ¤ — бинарная операция П2 ↦ П.

Соответствующая таблица Кэли для алгебры постановок Галуа имеет вид табл. 3.

Таблица 3

Таблица Кэли для алгебры подстановок Галуа

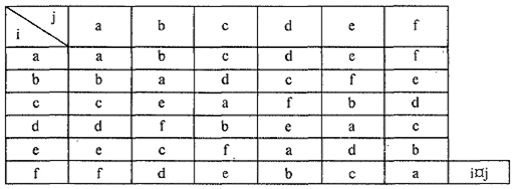
В такой алгебре выполняется закон ассоциативности, но не выполняется закон коммутативности.

Нейтральным элементом является подстановка а.

Группа — это полугруппа взаимно однозначных преобразований, причем именно однозначность гарантирует наличие обратного преобразования. Можно сказать, что в группе при любом числе умножений не теряется информация об исходном элементе: если известно, на что умножали, всегда можно узнать, что умножали. Для полугруппы это верно не всегда. Пусть дана дискретная система с конечным числом состояний S = { S 1..., Sn}, на вход которой может быть подано входное воздействие из множества х = {х1,..., х m}. Всякое входное воздействие однозначно переводит состояние системы в некоторое другое состояние, т. е. является преобразованием множества S . Последовательности воздействий — композиция преобразований, поэтому множество всех последовательностей — полугруппа с образующими {х1,..., х m}. Если такая полугруппа является группой, то по любой входной последовательности и заключительному состоянию системы можно однозначно определить ее начальное состояние.

Алгебра <М, ·, +>, которая по умножению (·) является мультипликативным группоидом, а по сложению (+) — абелевой группой, причем умножение связано со сложением законом дистрибутивности

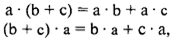
называется кольцом. Например, числовыми кольцами являются множество целых чисел, множество рациональных чисел, множество действительных чисел, множество комплексных чисел.

Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом (имеются обратные элементы по умножению). Тело, у которого мультипликативная группа абелева, называется полем. Таковы поля Галуа.

Алгебра множеств (алгебра Кантора)

Алгебра Кантора: < B ( I ), ∪ , ∩ , –>. Носителем ее является булеан универсального множества I , сигнатурой — операции объединения ∪ , пересечения ∩ и дополнения.

Для операций алгебры Кантора выполняются следующие законы:

1) коммутативности объединения и пересечения:

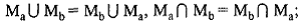
2) ассоциативности объединения и пересечения:

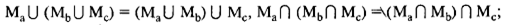
3) дистрибутивности пересечения относительно объединения и объединения относительно пересечения:

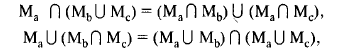
причем последнее соотношение не имеет аналога в обычной алгебре;

4) идемпотентности объединения и пересечения:

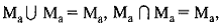
поэтому в алгебре Кантора нет ни степеней, ни коэффициентов;

5) де Моргана:

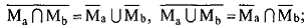
6) двойного дополнения:

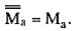
Выполнимы также следующие действия с универсальным I и пустым ∅ множествами:

7 )

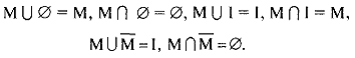
Все эти соотношения могут быть доказаны с использованием кругов Эйлера. Видна двойственность соотношений: они справедливы как относительно объединения, так и относительно пересечения.

Рассмотрим дополнительные законы:

8) склеивания:

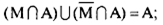
9) поглощения:

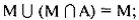
10) Порецкого — по фамилии российского логика, математика и астронома, профессора Казанского университета Платона Сергеевича Порецкого (1846–1907 гг.):

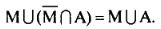
Алгебра Кантора по аддитивной операции объединения и мультипликативной операции пересечения является абелевой полугруппой, так как для этих операций выполняются законы коммутативности и ассоциативности, но она не является группой, поскольку уравнения 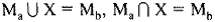не имеют решения, например, для случая, когда множества не пересекаются: 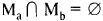. Поэтому алгебра Кантора по двухместным операциям ∩ и ∪ не является кольцом. Эта алгебра принадлежит к другому классу фундаментальных алгебр — к классу решеток.