Алгоритм середины квадрата

Он работает следующим образом. Значение ключа x возводится в квадрат (с двойной точностью, чтобы избежать переполнения разрядной сетки), а затем из двоичного представления результата вырезается такое количество средних разрядов, которое достаточно для представления индекса таблицы.

Суть алгоритма иллюстрируется на рис. 6.1, где принято, что значение ключа есть 16-разрядное число, его квадрат занимает 32 разряда, а для представления индекса используется 12 разрядов.

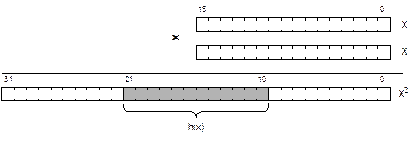
Рис. 6.1. Выделение середины квадрата ключа

Для данного алгоритма, в отличие от предыдущего, в качестве размера хеш-таблицы удобно выбрать некоторую степень двойки, например, 1 024, 4 096, 65 536 и т.п. При этом разряды, вырезанные из середины квадрата (соответственно, 10, 12, 16 разрядов), образуют готовое значение индекса.

Почему рекомендуется брать разряды из середины квадрата, а не младшие либо старшие разряды? Потому что на значение средних разрядов в равной степени влияют как младшие, так и старшие разряды ключа. Это позволяет рассеять некоторые виды неравномерностей. Например, если значительная часть ключей – небольшие числа в пределах, скажем, 2¹⁰, то их квадраты будут в пределах 2²⁰, т.е. старшие 12 разрядов будут содержать нулевые значения. И наоборот, если ключами являются числа, кратные некоторой степени двойки, то их квадраты будут содержать много нулей в младших разрядах. Использование средних разрядов позволяет избежать этих неприятностей (если нулей в ключе не слишком много).

В вычислительном отношении алгоритм середины квадрата также достаточно экономен. Фактически он требует одной команды целочисленного умножения, а затем команды сдвига средних разрядов вправо и команды конъюнкции для отбрасывания ненужных старших разрядов.

Недостатком алгоритма является то, что в случае большого количества нулей в младших или в старших разрядах ключа, результат может содержать много нулей даже в средних разрядах.

Алгоритм умножения

По сути, он отличается от предыдущего тем, что значение ключа умножается не на себя самого, а на некоторую числовую константу. Алгоритм может быть реализован очень эффективно, если учитывать особенности двоичного представления чисел в компьютере.

Первой операцией, которая выполняется в этом алгоритме, является умножение ключа x на константу C с отбрасыванием старших разрядов произведения, не уместившихся в разрядной сетке. Цель этой операции – рассеять ключи по всему множеству допустимых целых чисел. Вторая операция – переход от диапазона всех целых чисел к диапазону индексов хеш-таблицы. Для этого выполняют умножение числа на размер хеш-таблицы N, но из произведения выделяют только те разряды, которые выходят за разрядную сетку целых чисел. Очевидно, что число, образованное этими разрядами, будет находиться в пределах от 0 до N–1, причем, если результат первого умножения был равномерно рассеян по множеству целых чисел, то значение хеш-функции будет так же хорошо рассеяно по множеству индексов.

Описанные действия можно записать в виде формул с использованием операций mod и div, однако это намеренно не сделано, чтобы не создавать соблазна использовать mod и div на практике. На самом деле, все гораздо проще, особенно если размер хеш-таблицы N = 2^k. При выполнении умножения на константу C старшие разряды произведения просто отбрасываются, а вместо умножения на N с выделением переполняющих разрядов выполняют просто сдвиг числа вправо, так, чтобы оставить только k старших разрядов.

Работа алгоритма показана на рис. 6.2.

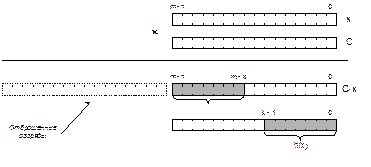
Рис. 6.2. Хеширование по алгоритму умножения

Как видно из рисунка, весь алгоритм сводится к одной операции умножения и одному сдвигу на m – k разрядов вправо.

Важную роль в алгоритме умножения играет константа-множитель C. В литературе (например, [5]) можно найти рекомендации по выбору значения C, основанные на глубоком анализе алгоритма с использованием методов теории чисел. Приведем здесь лишь несколько простых советов, позволяющих избежать грубых ошибок при выборе. (Предполагается, что размер хеш-таблицы N = 2^k.):

· значение C обязательно должно быть нечетным, а еще лучше – простым числом;

· не следует выбирать слишком маленькие значения; лучше, если C, по крайней мере, не меньше 1000;

· нежелательно также использовать числа, лишь на несколько единиц отличающиеся от одной из степеней двойки, например, такие, как 2 047 (почти равно 2¹¹ = 2 048) или 4 099 (близко к 2¹² = 4 096).